Gegeben ist die Funktion \(f \colon x \mapsto \sqrt{1 - \ln{x}}\) mit maximaler Definitionsmenge \(D\).

Bestimmen Sie \(D\).

(2 BE)

Lösung zu Teilaufgabe 1a

Maximale Definitionsmenge einer Funktion

\[f(x) = \sqrt{1 - \ln{x}}\]

1. Bedingung:

Der Radikand der Wurzel darf nicht negativ sein.

\[\begin{align*} \Longrightarrow \quad 1 - \ln x &\geq 0 & &| + \ln x \\[0.8em] 1 &\geq \ln x & &| \; e^{(\dots)} \enspace \text{(zur Basis} \; e \; \text{potenzieren)} \\[0.8em] e^{1} &\geq e^{\ln x} & &| \; a^{\log_{a}{x}} = x \\[0.8em] e &\geq x \end{align*}\]

2. Bedingung:

Die Natürliche Logarithmusfunktion \(x \mapsto \ln x\) ist in \(\mathbb R^{+}\) definiert.

\[\Longrightarrow \quad x > 0\]

Beide Bedingungen müssen erfüllt sein:

\[\Longrightarrow \quad 0 < x \enspace \wedge \enspace x \leq e\]

\[\Longrightarrow \quad D = \; ]0;e]\]

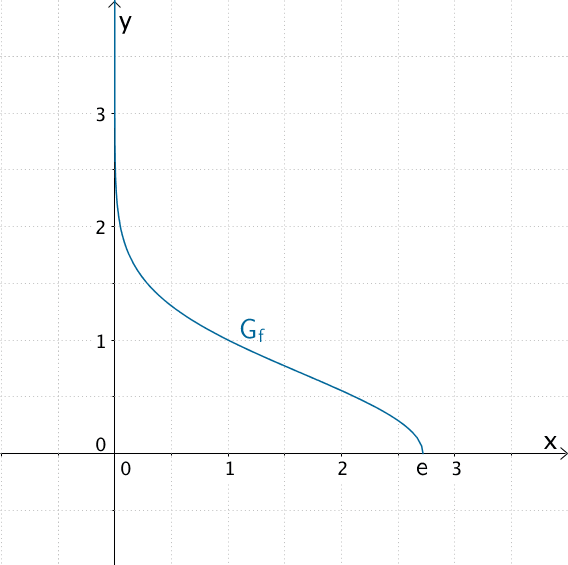
Graph der Funktion \(f \colon x \mapsto \sqrt{1 - \ln{x}}\) mit maximalem Definitionsbereich \(D = \; ]0;e]\)