Berechnen Sie den Wert des Integrals \(\displaystyle \int_1^2 f(x)dx\).
(3 BE)
Lösung zu Teilaufgabe 1b
\[f(x) = \frac{1}{x^2} + 1; \; D_f = \mathbb \backslash \{0\}\]

\[\int_a^b f(x)dx = \left[ F(x) \right]_a^b = F(b) - F(a)\]
Dabei ist \(F\) eine Stammfunktion von \(f\).
Die Berechnung eines bestimmten Integrals hängt maßgeblich davon ab, wie schwierig es ist, eine Stammfunktion des Integranden zu bilden.
Nachfolgend sind in diesem Zusammenhang wichtige unbestimmte Integrale aufgeführt (\(C \in \mathbb R\)):
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Ein bestimmtes Integral \(\displaystyle \int_a^b f(x)dx\) gibt die Flächenbilanz der Inhalte der Flächen an, die der Graph der Funktion \(f\) im Intervall \([a;b]\) mit der \(x\)-Achse einschließt.
Dabei zählen für \(a < b\) Flächen oberhalb der \(\textcolor{#0087c1}{x}\)-Achse positiv und Flächen unterhalb der \(\textcolor{#cc071e}{x}\)-Achse negativ. Für \(a > b\) zählen die Flächen mit umgekehrten Vorzeichen.
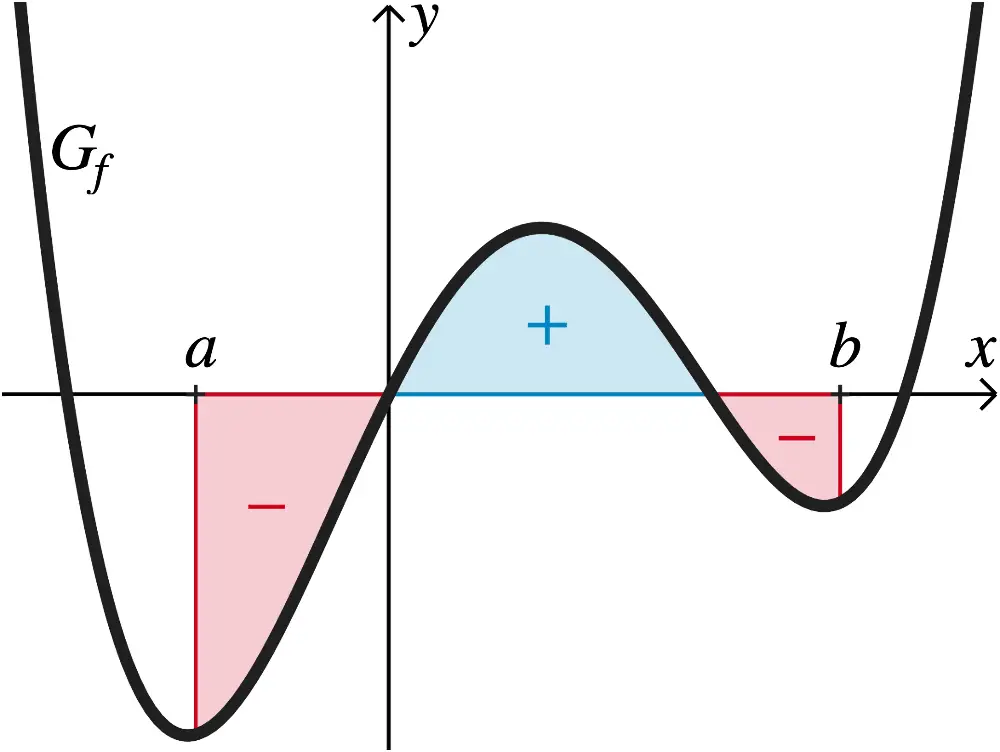
Identische Integrationsgrenzen:
\[\int_{\textcolor{#cc071e}{a}}^{\textcolor{#cc071e}{a}}f(x)dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} \textcolor{#e9b509}{k} \cdot f(x)dx = \textcolor{#e9b509}{k} \cdot \int_{a}^{b}f(x)dx\) mit \(\textcolor{#e9b509}{k} \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{\textcolor{#cc071e}{a}}^{\textcolor{#0087c1}{b}}f(x)\,dx = -\int_{\textcolor{#0087c1}{b}}^{\textcolor{#cc071e}{a}}f(x)\,dx\]
Zerlegung in Teilintervalle:
\[\displaystyle \int_{\textcolor{#cc071e}{a}}^{\textcolor{#0087c1}{b}}f(x)\,dx = \int_{\textcolor{#cc071e}{a}}^{\textcolor{#89ba17}{c}}f(x)\,dx + \int_{\textcolor{#89ba17}{c}}^{\textcolor{#0087c1}{b}}f(x)\,dx\]
Für die Berechnung des Werts des Integrals \(\displaystyle \int_1^2 f(x)dx\) wird eine Stammfunktion von \(f\) benötigt. Diese lässt sich einfacher bestimmen, wenn der Funktionsterm von \(f\) in der Potenzschreibweise formuliert wird.
\[\begin{align*}\int_1^2 f(x) dx &=\int_1^2 \left( \frac{1}{x^2}+1 \right)dx &&| \;\frac{1}{a^r} = a^{-r} \\[0.8em] &= \int_1^2 \left( \textcolor{#e9b509}{x^{-2} + 1} \right)dx &&\Big|\; \int \textcolor{#e9b509}{x^r} dx = \textcolor{#e9b509}{\frac{x^{r + 1}}{r + 1} + C} \;(r \neq -1) \\[0.8em] &= \left[ \textcolor{#e9b509}{-x^{-1} + x} \right]_{\textcolor{#cc071e}{1}}^{\textcolor{#0087c1}{2}} &&|\; a^{-r} = \frac{1}{a^r}\; \text{(optional)} \\[0.8em] &= \bigg[ \textcolor{#e9b509}{\underbrace{-\frac{1}{x} + x}_{\text{Stammfunktion}}} \bigg]_{\textcolor{#cc071e}{1}}^{\textcolor{#0087c1}{2}} \\[0.8em] &= -\frac{1}{\textcolor{#0087c1}{2}} + \textcolor{#0087c1}{2} - \left( -\frac{1}{\textcolor{#cc071e}{1}} + \textcolor{#cc071e}{1} \right)\\[0.8em] &= \frac{3}{2}\end{align*}\]


