Ist das Sperrtor geöffnet, so liegt dessen rechteckige Seitenfläche unterhalb der Wasseroberfläche und ist parallel zu ihr (vgl. Abbildung 2a). Ist das Sperrtor geschlossen, so steht die Seitenfläche senkrecht zur Wasseroberfläche (vgl. Abbildung 2b).
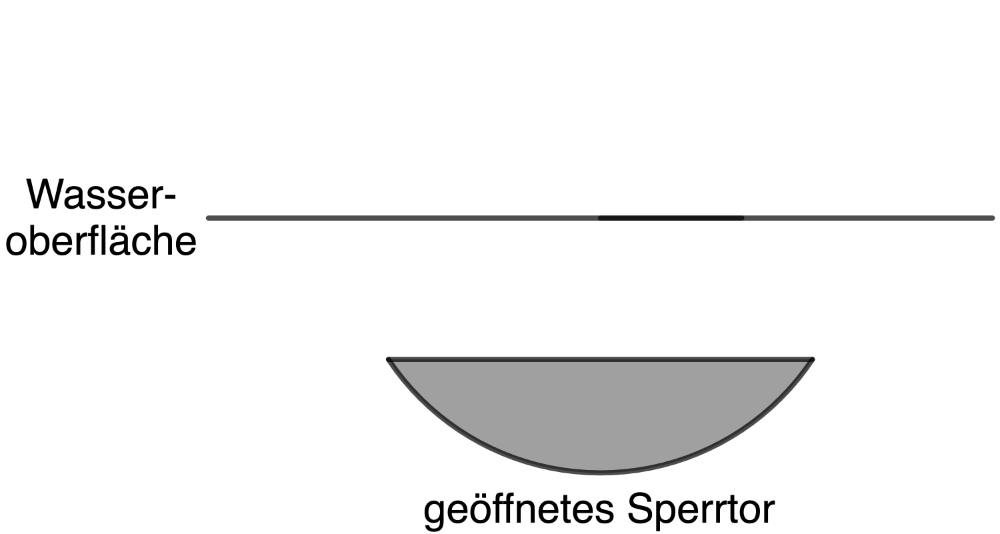 Abb. 2a
Abb. 2a
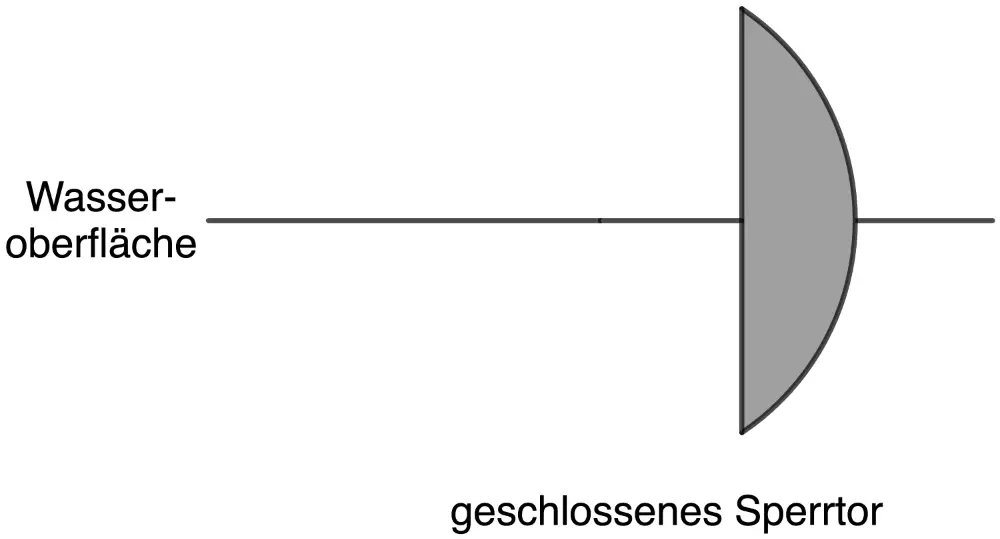 Abb. 2b
Abb. 2b
Dei einem Schließvorgang wird das geöffnete Sperrtor durch eine Vierteldrehung der Metallscheiben mit konstanter Geschwindigkeit innerhalb von 15 Minuten geschlossen.
Zu einem bestimmten Zeitpunkt während des Schließvorgangs befinden sich erstmals Teile des Sperrtors an der Wasseroberfläche. Bestimmen Sie mithilfe des Ergebnisses von Aufgabe c die Zeit, die ab diesem Zeitpunkt bis zum Ende des Schließvorgangs vergeht.
(3 BE)
Lösung zu Teilaufgabe e
\(t = \dfrac{90^{\circ} - 33{,}7^{\circ}}{90^{\circ}} \cdot 15\,\textsf{min} = 9{,}38\,\textsf{min} = 9\,\textsf{min}\;23\,\textsf{s}\)
Ausführliche Erklärung (nicht verlangt)
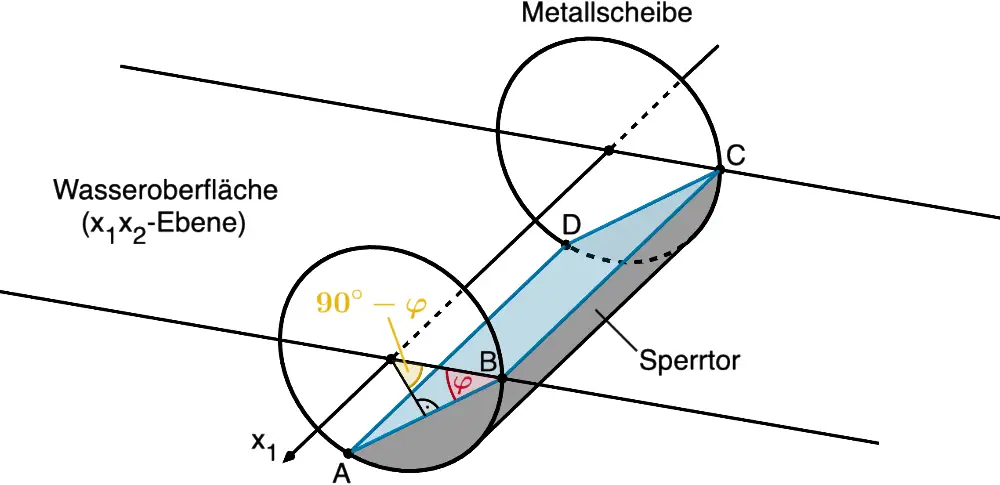 Abb. 1, ergänzende Eintragungen
Abb. 1, ergänzende Eintragungen
Abbildung 1 zeigt den Schließvorgang zum Zeitpunkt, zu dem sich erstmals Teile des Sperrtors an der Wasseroberfläche befinden (Kante \([BC]\)). Zu diesem Zeitpunkt ist die rechteckige Seitenfläche des Sperrtors (Rechteck \(ABCD\), Ebene \(\textcolor{#0087c1}{E}\)) um den Winkel \(\textcolor{#cc071e}{\varphi}\) gegenüber der Wasseroberfläche (\(x_1x_2\)-Ebene) geneigt (vgl. Teilaufgabe c).
Wie abgebildet, lässt sich ein rechtwinkliges Dreieck konstruieren, in dem der Winkel \(\textcolor{#e9b509}{90^{\circ} - \varphi}\) der Drehung bis zum Ende des Schließvorgangs entspricht.
Da sich das Sperrtor während eines vollständigen Schließvorgangs innerhalb von 15 min mit konstanter Geschwindigkeit um 90° dreht, lässt sich die verbleibende Zeit anteilig mithilfe der verbleibenden Drehung um \(\textcolor{#e9b509}{90^{\circ} - \varphi}\) berechnen.
\(\varphi \approx 33{,}7^{\circ}\) (vgl. Teilaufgabe c)
\[t = \frac{\textcolor{#e9b509}{90^{\circ} - \varphi}}{90^{\circ}} \cdot 15\,\textsf{min} = \frac{90^{\circ} - 33{,}7^{\circ}}{90^{\circ}} \cdot 15\,\textsf{min} = 9{,}38\,\textsf{min}\]
\(9{,}38\,\textsf{min} = 9\,\textsf{min}\) und \(0{,}38 \cdot 60\,\textsf{s} \approx 23\,\textsf{s}\)


