Viele Zufallsexperimente lassen sich durch das Ziehen aus einer Urne mit nur schwarzen und weißen Kugel simulieren. Das heißt, es sind nicht mehr alle Kugel unterscheidbar und die Reihenfolge des Ziehens wird folglich nicht beachtet. Entscheidend für die Wahrscheinlichkeitsberechnungen ist vielmehr, ob das Ziehen mit oder ohne Zurücklegen erfolgt.
Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge
Beim Ziehen ohne Zurücklegen aus einer Urne mit nur schwarzen und weißen Kugeln ändert sich bei jedem Zug die Wahrscheinlichkeit, eine schwarze Kugel (bzw. eine weiße Kugel) zu ziehen. Ohne Beachtung der Reihenfolge entspricht dies dem Ziehen mit einem Griff (vgl. Abiturskript - 3.2.1 Grundformeln der Kombinatorik).
Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
(vgl. Merkhilfe)
Allgemeine Betrachtung für ein Ereignis \(A\):
\(N\): Anzahl der vorliegenden (gleichartigen) Elemente insgesamt
\(n\): Anzahl der entnommenen bzw. ausgewählten Elemente (Umfang der Stichprobe)
\(K\): Anzahl der Elemente mit der Eigenschaft \(A\)
\(k\): Anzahl der Elemente in der Stichprobe mit der Eigenschaft \(A\)
Der Binomialkoeffizient \(\displaystyle \binom{N}{n}\) beschreibt die Anzahl aller gleichwahrscheinlichen Möglichkeiten (Ergebnisse), \(n\) Elemente der Stichprobe aus \(N\) vorliegenden Elementen zu entnehmen bzw. auszuwählen. Das heißt, es liegt ein Laplace-Experiment vor (vgl. Abiturskript - 3.1.3 Laplace-Experiment, Laplace-Wahrscheinlichkeit).
Der Binomialkoeffizient \(\displaystyle \binom{K}{k}\) beschreibt die Anzahl der Möglichkeiten, \(k\) Elemente der Stichprobe mit der Eigenschaft \(A\) aus \(K\) vorhandenen Elementen mit der Eigenschaft \(A\) zu entnehmen bzw. auszuwählen. Kurz gesagt: Die Anzahl der auf das Ereignis \(A\) bezogenen möglichen Treffer.
Der Binomialkoeffizient \(\displaystyle \binom{N - K}{n - k}\) beschreibt die Anzahl der Möglichkeiten, \(n - k\) Elemente der Stichprobe ohne der Eigenschaft \(A\) aus \(N - K\) vorhandenen Elementen ohne der Eigenschaft \(A\) zu entnehmen bzw. auszuwählen. Kurz gesagt: Die Anzahl der auf das Ereignis \(A\) bezogenen möglichen Nicht-Treffer bzw. Nieten.
Der Term \(\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}\) beschreibt nach dem Zählprinzip die Anzahl der für das Ereignis \(A\) günstigen Möglichkeiten.
\[P(\text{„genau}\,k\,\text{Treffer"}) = \frac{\displaystyle \overbrace{\overbrace{\binom{K}{k}}^{\large \text{Treffer}} \cdot \overbrace{\binom{N - K}{n - k}}^{\large \text{Nieten}}}^{\large \text{Anzahl der günstigen Möglichkeiten}}}{\displaystyle \underbrace{\binom{N}{n}}_{\large \text{Anzahl aller Möglichkeiten}}}\]
Beim Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge ändert sich die Wahrscheinlichkeit für einen Treffer bei jedem Zug. Für eine genügend große Anzahl \(N\) bzw. eine genügend kleine Anzahl \(n\) \((N \gg n)\) ist diese Änderung jedoch gering.
Als Faustregel gilt: Ist die Bedingung \(n < 0{,}05 N\) (Stichprobenumfang kleiner als 5 %) erfüllt, kann die Wahrscheinlichkeit \(P(\text{„genau}\,k\,\text{Treffer"})\) näherungsweise nach dem Urnenmodell Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge berechnet werden.
Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge
Beim Ziehen mit Zurücklegen aus einer Urne mit nur schwarzen und weißen Kugeln bleibt die Wahrscheinlichkeit, eine schwarze Kugel (oder eine weiße Kugel) zu ziehen, bei jedem Zug konstant (vgl. Abiturskript - 3.3.3 Binomialverteilte Zufallsgröße).
Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge
Werden aus einer Urne, in der der Anteil schwarzer Kugeln \(p\) ist, \(n\) Kugeln mit Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\]
(vgl. Merkhilfe)
Allgemeine Betrachtung für ein Ereignis \(A\):
\(p\): konstante Trefferwarscheinlichkeit für das Ereignis \(A\)
\(k\): Anzahl der Treffer bezogen auf das Ereignis \(A\)
\(n\): Anzahl der Wiederholungen bzw. Umfang der Stichprobe
Der Term \(p^{k} \cdot (1 - p)^{n - k}\) beschreibt die Wahrscheinlichkeit für genau eine mögliche Abfolge von \(k\) auf das Ereignis \(A\) bezogenen Treffern unter \(n\) Wiederholungen eines Zufallsexperiments.
Der Binomialkoeffizient \(\displaystyle \binom{n}{k}\) beschreibt die Anzahl der Möglichkeiten, wie die \(k\) auf das Ereignis \(A\) bezogenen Treffer unter den \(n\) Wiederholungen eines Zufallsexperiments verteilt sein können.
\[P(\text{„genau}\,k\,\text{Treffer"}) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\]
{zen-warning}Spielt die Reihenfolge der \(k\) Treffer unter den \(n\) Wiederholungen eine Rolle, kann die Formel nicht angewendet werden (vgl. 2. Beispielaufgabe, Ereignisse \(D\), \(E\)){/zen-warning}
Beispielaufgaben
1. Beispielaufgabe
Eine Lieferung enthält 200 Transistoren. Diese stammen aus einer Massenfertigung mit 5 % Ausschussanteil. Bei der Anlieferung wird eine Abnahmekontrolle durchgeführt. Zu diesem Zweck wird der Lieferung eine Stichprobe von 5 Transistoren entnommen und die Transistoren auf ihre Funktion hin überprüft. Berechnen Sie die Wahrscheinlichkeit der folgenden Ereignisse:
\(A\): „Alle Transistoren sind funktionstauglich."
\(B\): „Genau ein Transistor ist defekt."
\(C\): „Mindestens ein Transistor ist defekt."
\(D\): „Höchstens ein Transistor ist defekt."
Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge, da die Transistoren der Lieferung einmalig entnommen werden und die Reihenfolge der Entnahme keine Rolle spielt.
Bei einem Ausschussanteil von 5 % sind 10 von den 200 angelieferten Transistoren defekt.
Wahrscheinlichkeit für das Ereignis \(A\)
\(A\): „Alle Transistoren sind funktionstauglich."
\(N\): 200 angelieferte Transistoren
\(n\): 5 für die Abnahmekontrolle entnommene Transistoren (Stichprobenumfang)
\(K\): 10 defekte Transistoren (5 % von 200)
\(k\): 0 defekte Transistoren unter der Stichprobe
\[\begin{align*} P(A) &= \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}} \\[0.8em] &= \frac{\displaystyle \binom{10}{0} \cdot \binom{200 - 10}{5 - 0}}{\displaystyle \binom{200}{5}} \\[0.8em] &= \frac{\displaystyle \binom{10}{0} \cdot \binom{190}{5}}{\displaystyle \binom{200}{5}} \\[0.8em] &\approx 0{,}772 \\[0.8em] &= 77{,}2\,\% \end{align*}\]
Wahrscheinlichkeit für das Ereignis \(B\)
\(B\): „Genau ein Transistor ist defekt."
\(N\): 200 angelieferte Transistoren
\(n\): 5 für die Abnahmekontrolle entnommene Transistoren (Stichprobenumfang)
\(K\): 10 defekte Transistoren (5 % von 200)
\(k\): 1 defekter Transistor unter der Stichprobe
\[\begin{align*} P(B) &= \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}} \\[0.8em] &= \frac{\displaystyle \binom{10}{1} \cdot \binom{200 - 10}{5 - 1}}{\displaystyle \binom{200}{5}} \\[0.8em] &= \frac{\displaystyle \binom{10}{1} \cdot \binom{190}{4}}{\displaystyle \binom{200}{5}} \\[0.8em] &\approx 0{,}208 \\[0.8em] &= 20{,}8\,\% \end{align*}\]
Wahrscheinlichkeit für das Ereignis \(C\)
\(C\): „Mindestens ein Transistor ist defekt."
Für die Berechnung der Wahrscheinlichkeit des Ereignisses \(C\): „Mindestens ein Transistor ist defekt." wird das Gegenereignis \(\overline{A} = \Omega \backslash A\): „Nicht alle Transistoren sind funktionstauglich." betrachtet.
Andernfalls müsste unter wesentlich größerem Rechenaufwand die Summe der Wahrscheinlichkeiten der Ereignisse „Ein Transistor ist defekt", „Zwei Transistoren sind defekt", ..., „Fünf Transistoren sind defekt", errechnet werden.
\[\begin{align*}P(C) &= 1 - P(A) \\[0.8em] &= 1 - \frac{\displaystyle \binom{10}{0} \cdot \binom{200 - 10}{5 - 0}}{\displaystyle \binom{200}{5}} \\[0.8em] &\approx 0{,}228 \\[0.8em] &= 22{,}8\,\% \end{align*}\]
Wahrscheinlichkeit des Ereignisses \(D\)
\(D\): „Höchstens ein Transistor ist defekt."
Das Ereignis \(D\): „Höchstens ein Transistor ist defekt." bedeute, dass keiner \((A)\) oder einer \((B)\) der fünf entnommenen Transistoren defekt ist.
\[\begin{align*} P(D) \enspace = \; \quad &P(A) + P(B) \\[0.8em] = \; \quad &\frac{\displaystyle \binom{10}{0} \cdot \binom{200 - 10}{5 - 0}}{\displaystyle \binom{200}{5}} \\[0.8em] + \, &\frac{\displaystyle \binom{10}{1} \cdot \binom{200 - 10}{5 - 1}}{\displaystyle \binom{200}{5}} \\[0.8em] \approx \; \quad &0{,}979 \\[0.8em] = \; \quad &97{,}9\,\% \end{align*}\]
2. Beispielaufgabe
Eine Firma stellt in sehr großer Stückzahl (Massenfertigung) Transistoren her. Aus laufender Qualitätskontrolle ist bekannt, dass 2 % aller produzierten Transistoren Ausschuss sind. Es werden 20 Transistoren für die tägliche Qualitätskontrolle entnommen. Berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
\(A\): „Alle Transistoren sind funktionstauglich."
\(B\): „Genau 3 Transistoren sind defekt."
\(C\): „Mindestens ein Transistor ist defekt."
\(D\): „Nur die ersten drei kontrollierten Transistoren sind defekt."
\(E\): „Drei hintereinander kontrollierte Transistoren sind defekt"
Da angenommen werden darf, dass die entnommene Stichprobe von \(n = 20\) Transistoren im Verhältnis zur Tagesproduktion gering ist, kann mit der konstanten Wahrscheinlichkeit \(p = 0{,}02\) für einen defekten Transistor gerechnet werden.
Wahrscheinlichkeit für das Ereignis \(A\)
\(n = 20\), \(p = 0{,}02\)
\(A\): „Alle Transistoren sind funktionstauglich."
\[\Longrightarrow \quad k = 0\]
\[\begin{align*}P(A) &= \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \\[0.8em] &= \binom{20}{0} \cdot {0{,}02}^{0} \cdot (1 - 0{,}02)^{20 - 0} \\[0.8em] &= 1 \cdot 1 \cdot {0{,}98}^{20} \\[0.8em] &\approx 0{,}6676 \\[0.8em] &= 66{,}76\,\% \end{align*}\]
Wahrscheinlichkeit für das Ereignis \(B\)
\(n = 20\), \(p = 0{,}02\)
\(B\): „Genau 3 Transistoren sind defekt."
\[\Longrightarrow \quad k = 3\]
\[\begin{align*}P(A) &= \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \\[0.8em] &= \binom{20}{3} \cdot {0{,}02}^{3} \cdot (1 - 0{,}02)^{20 - 3} \\[0.8em] &= 1140 \cdot {0{,}02}^{3} \cdot {0{,}98}^{17} \\[0.8em] &\approx 0{,}0065 \\[0.8em] &= 0{,}65\,\% \end{align*}\]
Wahrscheinlichkeit für das Ereignis \(C\)
\(n = 20\), \(p = 0{,}02\)
\(C\): „Mindestens ein Transistor ist defekt."
Für die Berechnung der Wahrscheinlichkeit des Ereignisses \(C\): „Mindestens ein Transistor ist defekt." wird das Gegenereignis \(\overline{A} = \Omega \backslash A\): „Nicht alle Transistoren sind funktionstauglich." betrachtet.
Andernfalls müsste unter wesentlich größerem Rechenaufwand die Summe der Wahrscheinlichkeiten der Ereignisse „Ein Transistor ist defekt", „Zwei Transistoren sind defekt", ..., „20 Transistoren sind defekt", errechnet werden.
\[\begin{align*} P(C) &= 1 - P(A) \\[0.8em] &= 1 - {0{,}98}^{20} \\[0.8em] &\approx 0{,}3324 \\[0.8em] &= 33{,}24\,\% \end{align*}\]
Wahrscheinlichkeit für das Ereignis \(D\)
\(n = 20\), \(p = 0{,}02\)
\(D\): „Nur die ersten drei kontrollierten Transistoren sind defekt."
Das Ereignis \(D\): „Nur die ersten drei kontrollierten Transistoren sind defekt." formuliert eine Bedingung für die Reihenfolge der \(k = 3\) Treffer. Die Formel \(\displaystyle P(\text{„genau}\,k\,\text{Treffer"}) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\) kann nicht angewendet werden, denn der Binomialkoeffizient \(\displaystyle \binom{20}{3}\) würde die Anzahl aller Möglichkeiten berücksichtigen wie die 3 defekten Transistoren unter den 20 kontrollierten Transistoren verteilt sein können.
\[\begin{align*}P(D) &= \underset{\large \text{1. Transistor}}{p} \cdot \underset{\large \text{2. Transistor}}{p} \cdot \underset{\large \text{3. Transistor}}{p} \cdot \underset{\large \text{4. bis 20. Transistor}}{(1 - p)^{17}} \\[0.8em] &= p^{3} \cdot (1 - p)^{17} \\[0.8em] &= {0{,}02}^{3} \cdot (1 - 0{,}02)^{17} \\[0.8em] &= {0{,}02}^{3} \cdot {0{,}98}^{17} \\[0.8em] &\approx 5{,}7 \cdot {10}^{-6} \\[0.8em] &= 5{,}7 \cdot {10}^{-4}\,\% \end{align*}\]
Anmerkung: Jede andere Reihenfolge von drei defekten Transistoren unter den 20 kontrollierten Transistoren führt ebenfalls auf den Term \(p^{3} \cdot (1 - p)^{17}\).
Wahrscheinlichkeit für das Ereignis \(E\)
\(n = 20\), \(p = 0{,}02\)
\(E\): „Drei hintereinander kontrollierte Transistoren sind defekt"
Das Ereignis \(E\): „Drei hintereinander kontrollierte Transistoren sind defekt" formuliert wie das Ereignis \(D\) eine Bedingung für die Reihenfolge der \(k = 3\) Treffer. Allerdings gibt es im Falle des Ereignisses \(E\) mehrere Möglichkeiten dafür, dass drei hintereinander kontrollierte Transistoren defekt sind.
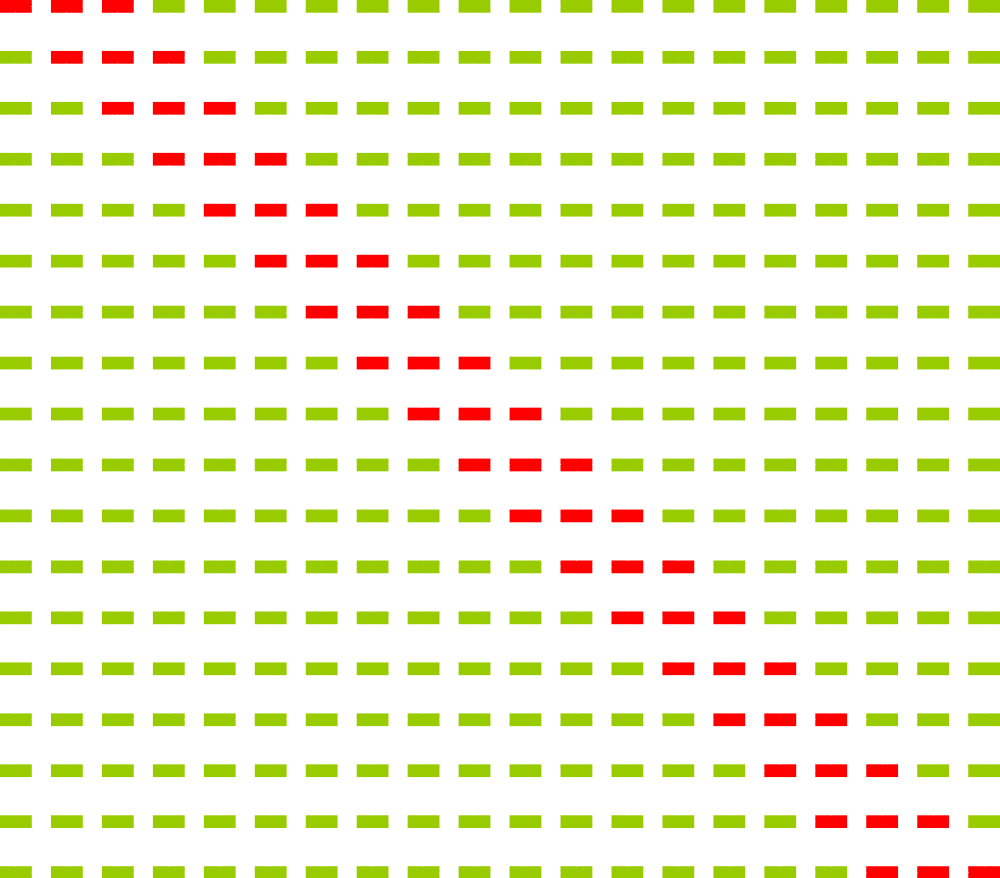
Veranschaulichung der 18 Möglichkeiten, dass von insgesamt 20 kontrollierten Transistoren 3 hintereinander kontrollierte Transistoren defekt sind.
Anmerkung: Für \(n \geq k\) gibt es \(n - k +1\) Möglichkeiten, eine Teilmenge von \(k\) Objekten hintereinander und ohne Berücksichtigung deren Reihenfolge (ohne Unterscheidung) auf \(n\) Objekte zu verteilen.
\[n - k + 1 = 20 - 3 + 1 = 18\]
\[\begin{align*}P(E) &= 18 \cdot P(D) \\[0.8em] &= 18 \cdot {0{,}02}^{3} \cdot {0{,}98}^{17} \\[0.8em] &\approx 1{,}0 \cdot {10}^{-4} \\[0.8em] &= 0{,}010\,\% \end{align*}\]


