Haben zu Beobachtungsbeginn Sonnenblumen der Sorte Tramonto die gleiche Höhe wie Sonnenblumen der Sorte Alba, so erreichen von da an die Sonnenblumen der Sorte Tramonto im Vergleich zu denen der Sorte Alba jede Höhe in der Hälfte der Zeit.
Das Wachstum von Sonnenblumen der Sorte Tramonto lässt sich modellhaft mithilfe einer in \(\mathbb R\) definierten Funktion \(g\) beschreiben, die eine Funktionsgleichung der Form I, II, oder III mit \(k \in \mathbb R^+\) besitzt:
\[\textsf{I}\enspace y = \frac{2e^{x+k}}{e^{x+k}+9}\]
\[\textsf{II}\enspace y = k \cdot \frac{2e^x}{e^x + 9}\]
\[\textsf{III}\enspace y = \frac{2e^{kx}}{e^{kx} + 9}\]
Dabei ist \(x\) die seit Beobachtungsbeginn vergangene Zeit in Monaten und \(y\) ein Näherungswert für die Höhe einer Blume in Metern.
Begründen Sie, dass weder eine Gleichung der Form I noch eine der Form II als Funktionsgleichung von \(g\) infrage kommt.
(4 BE)
Lösung zu Teilaufgabe 2e
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
Das beschriebene Wachstum von Sonnenblumen der Sorte Tramonto entspricht einer Stauchung (Streckungsfaktor: (\(0 < \frac{1}{k} < 1\)) des Graphen der Wachstumsfunktion \(f\) von Sonnenblumen der Sorte Alba (siehe Teilaufgaben 2a,b,c) in Richtung der Zeitachse (\(x\)-Achse).
Ausschluss einer Gleichung der Form I
\[\textsf{I}\enspace y = \frac{2e^{x+k}}{e^{x+k}+9}\,; \quad k \in \mathbb R^+\]
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
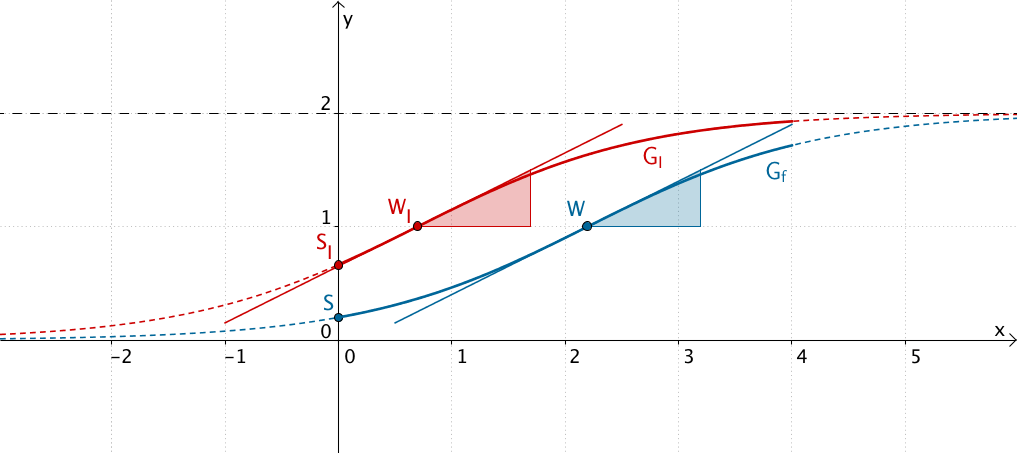
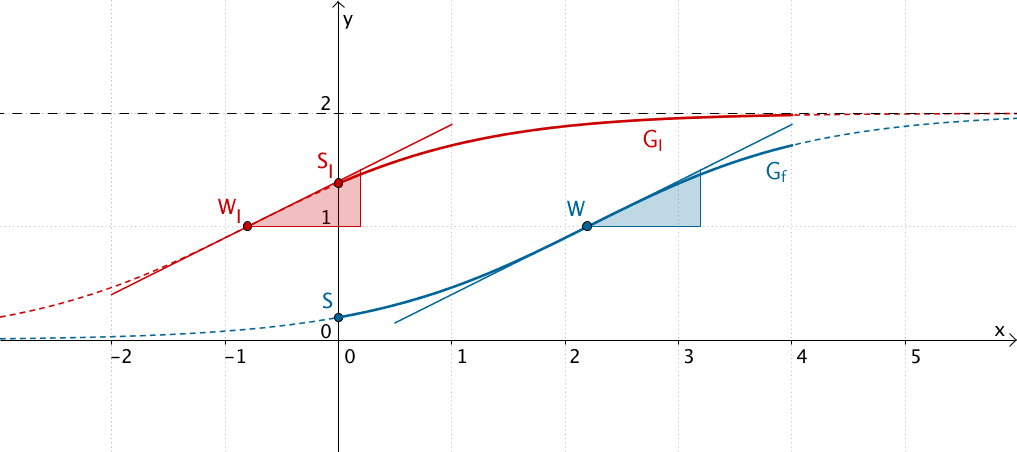
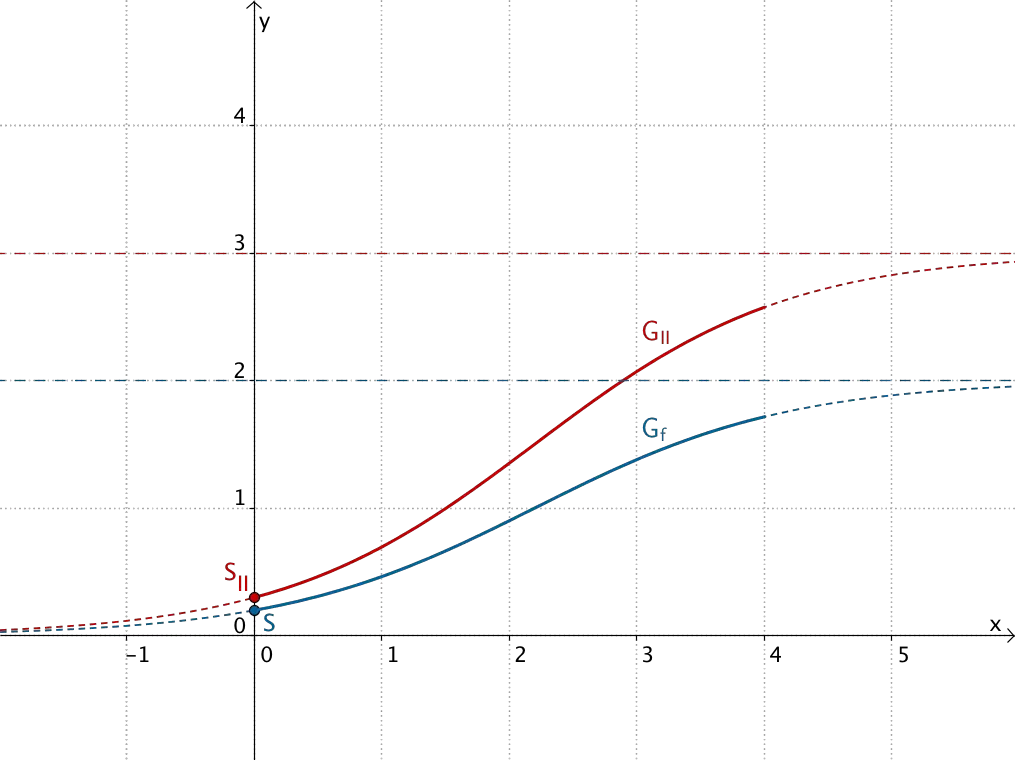
Eine Gleichung der Form I bewirkt eine Verschiebung des Graphen der Funktion \(f\) (Sonnenblumen der Sorte Alba) um \(-k\) in \(x\)-Richtung.
Daraus folgt:
- Keine gleiche Höhe der beiden Sorten zu Beobachtungsbeginn
- Keine erhöhte Wachstumsrate der Sorte Tramonto
Eine Gleichung der Form I kommt somit nicht in Frage.
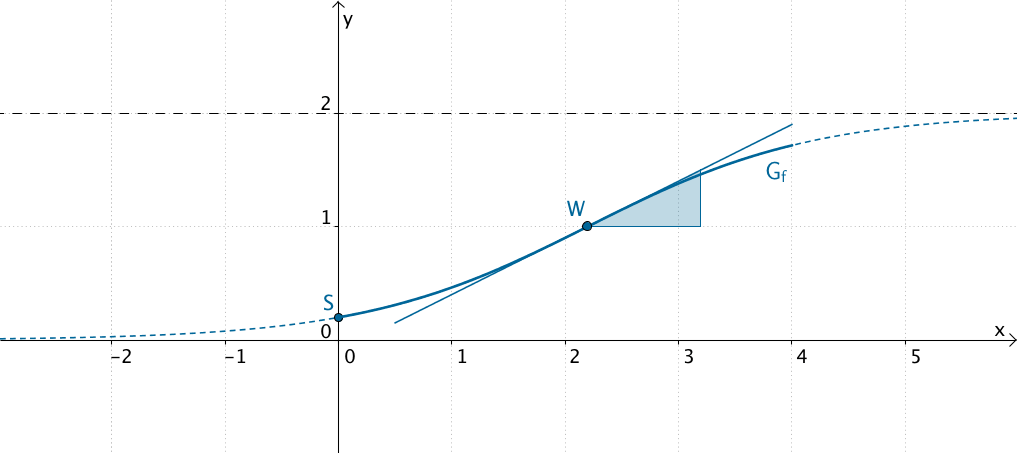
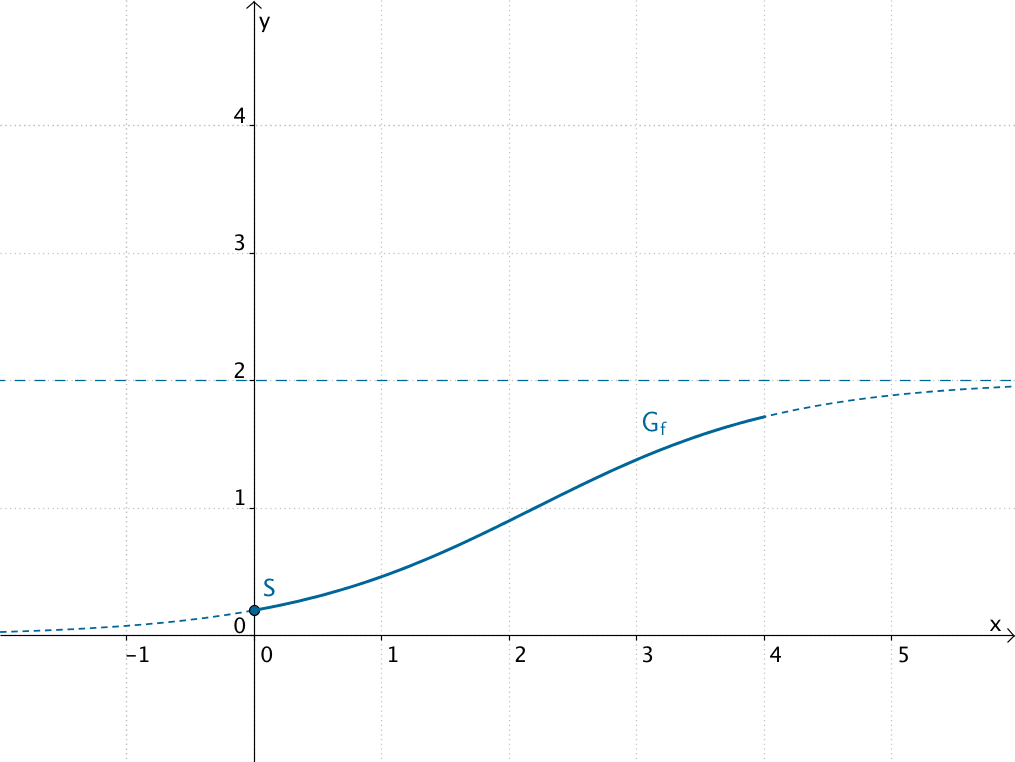
Graph der Funktion \(\textcolor{#0087c1}{f \colon x \mapsto \dfrac{2e^{x}}{e^{x} + 9}; \;x \in [0;4]}\) sowie
Graphen der Funktionen \(x \mapsto \dfrac{2e^{x+\textcolor{#cc071e}{k}}}{e^{x+\textcolor{#cc071e}{k}}+9}; \; D = \mathbb R\) für \(\textcolor{#cc071e}{k} = \{\textcolor{#cc071e}{1{,}5};\textcolor{#cc071e}{3};\textcolor{#cc071e}{4}\}\)
Ausschluss einer Gleichung der Form II
\[\textsf{II} \enspace y = k \cdot \frac{2e^x}{e^x + 9}\,; \quad k \in \mathbb R^+\]
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
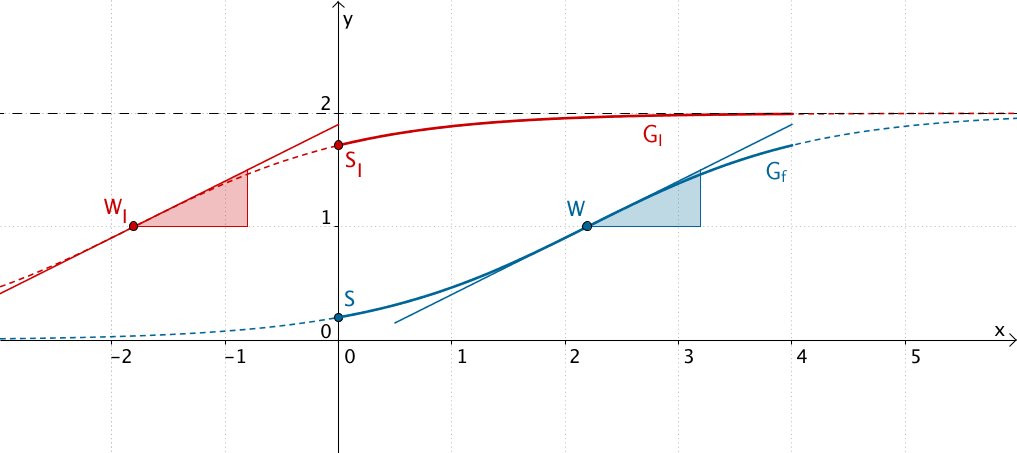
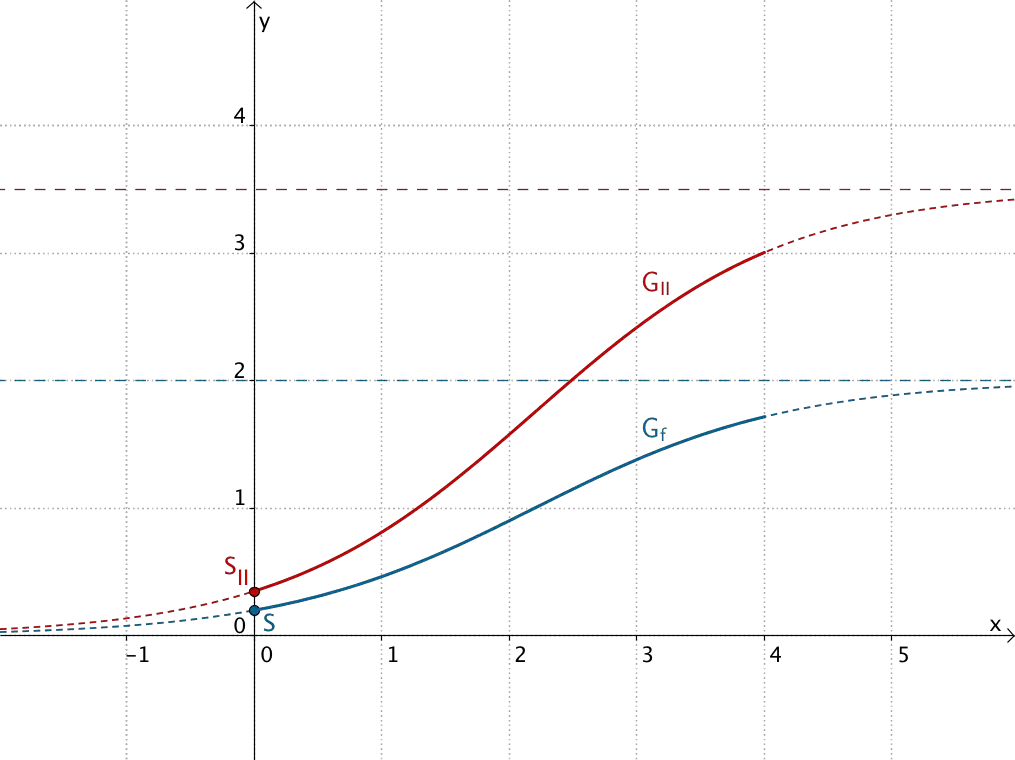
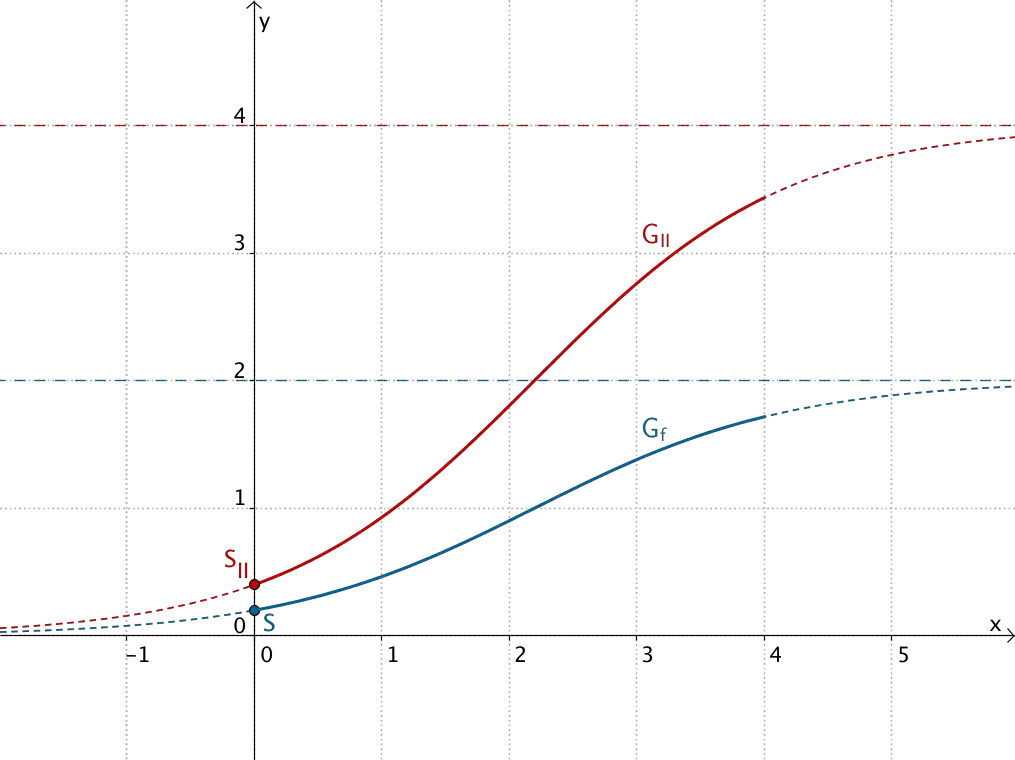
Eine Gleichung der Form II bewirkt eine Streckung des Graphen der Funktion \(f\) (Sonnenblumen der Sorte Alba) mit dem Streckungsfaktor \(k\) in \(y\)-Richtung.
Daraus folgt:
- Keine gleiche Höhe der beiden Sorten zu Beobachtungsbeginn
- Unendliche Höhe \(k \cdot f(4)\) mit \(k \in \mathbb R^{+}\) der Sonnenblumen der Sorte Tramonto nach vier Monaten
Eine Gleichung der Form II kommt somit nicht in Frage.
Graph der Funktion \(\textcolor{#0087c1}{f \colon x \mapsto \dfrac{2e^{x}}{e^{x} + 9}; \; x \in [0;4]}\) sowie
Graphen der Funktionen \(x \mapsto \textcolor{#cc071e}{k} \cdot \dfrac{2e^{x}}{e^{x} +9}; \; D = \mathbb R\) für \(\textcolor{#cc071e}{k} = \{\textcolor{#cc071e}{1{,}5};\textcolor{#cc071e}{1{,}75};\textcolor{#cc071e}{2}\}\)