- Details
- Kategorie: Analysis 1
Geben Sie für die Funktionen \(f_{1}\) und \(f_{2}\) jeweils die maximale Definitionsmenge und die Nullstelle an.
\[f_{1} \colon x \mapsto \frac{2x + 3}{x^{2} - 4}\]
\[f_{2} \colon x \mapsto \ln{(x + 2)}\]
(4 BE)
- Details
- Kategorie: Analysis 1
Geben Sie den Term einer in \(\mathbb R\) definierten Funktion an, deren Graph im Punkt \((2|1)\) eine waagrechte Tangente, aber keinen Extrempunkt hat.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = -x^{3} + 9x^{2} -15x -25\). Weisen Sie nach, dass \(f\) folgende Eigenschaften besitzt:
(1) Der Graph von \(f\) besitzt an der Stelle \(x = 0\) die Steigung \(-15\).
(2) Der Graph von \(f\) besitzt im Punkt \(A(5|f(5))\) die \(x\)-Achse als Tangente.
(3) Die Tangente \(t\) an den Graphen der Funktion \(f\) im Punkt \(B(-1|f(-1))\) kann durch die Gleichung \(y = -36x - 36\) beschrieben werden.
(5 BE)
- Details
- Kategorie: Analysis 1
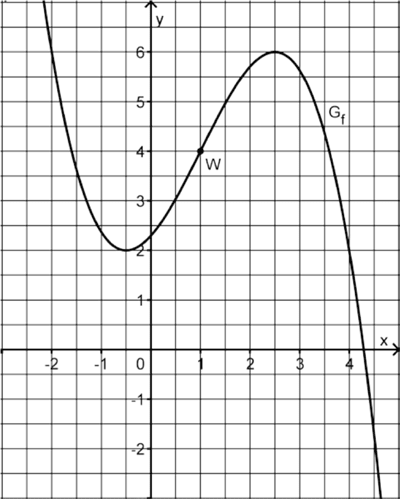
Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f\) mit dem Wendepunkt \(W(1|4)\).
Ermitteln Sie mithilfe der Abbildung näherungsweise den Wert der Ableitung von \(f\) an der Stelle \(x = 1\).
Skizzieren Sie den Graphen der Ableitungsfunktion \(f'\) von \(f\) in die Abbildung; berücksichtigen Sie dabei insbesondere die Lage der Nullstellen von \(f'\) sowie den für \(f'(1)\) ermittelten Näherungswert.
(3 BE)
- Details
- Kategorie: Analysis 1
Für jeden Wert von \(a\) mit \(a \in \mathbb R^{+}\) ist eine Funktion \(f_{a}\) durch \(f_{a}(x) = \dfrac{1}{a} \cdot x^{3} - x\) mit \(x \in \mathbb R\) gegeben.
Eine der beiden Abbildungen stellt einen Graphen von \(f_{a}\) dar. Geben Sie an, für welche Abbildung dies zutrifft. Begründen Sie Ihre Antwort.
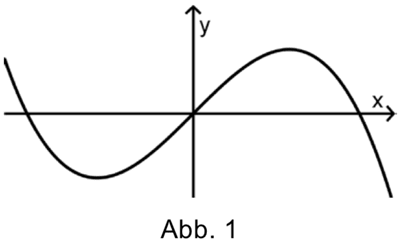
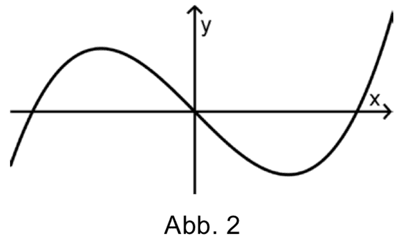
(2 BE)
- Details
- Kategorie: Analysis 1
Für jeden Wert von \(a\) besitzt der Graph von \(f_{a}\) genau zwei Extrempunkte. Ermitteln Sie denjenigen Wert von \(a\), für den der Graph der Funktion \(f_{a}\) an der Stelle \(x = 3\) einen Extrempunkt hat.
(3 BE)


