Skizzieren Sie in die Abbildung den Graphen von \(F\). Berücksichtigen Sie dabei insbesondere, dass \(F(1) \approx 3{,}5\) und \(\lim \limits_{x\,\to\,+\infty} F(x) = 2\) gilt.
(3 BE)
Lösung zu Teilaufgabe 1e
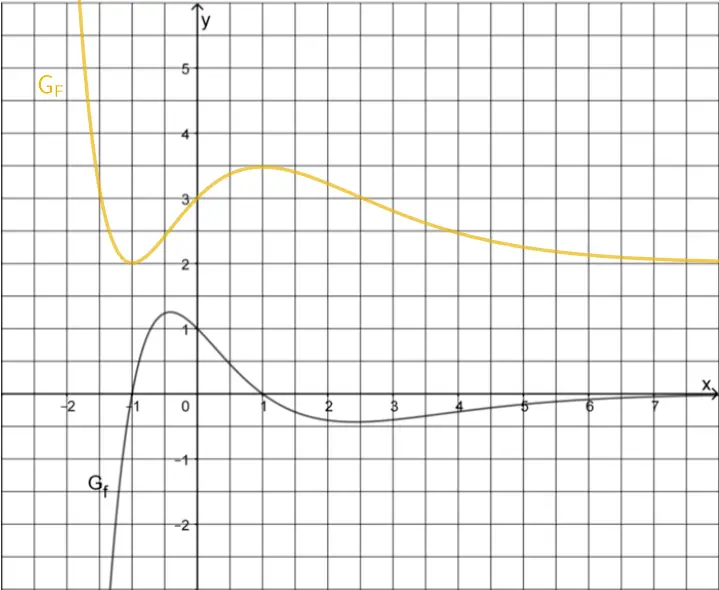
Skizze des Graphen der Stammfunktion \(F\)
Die Skizze sollte mindestens berücksichtigen, dass
- \(\textcolor{#e9b509}{T(-1|2)}\) ein Tiefpunkt von \(\textcolor{#e9b509}{G_{F}}\) ist (vgl. Teilaufgabe 1d),
- der Punkt \(\textcolor{#e9b509}{(1|F(1))}\) mit \(\textcolor{#e9b509}{F(1) \approx 3{,}5}\) ein Hochpunkt von \(\textcolor{#e9b509}{G_{F}}\) ist und
- \(\textcolor{#e9b509}{G_{F}}\) sich wegen \(\textcolor{#e9b509}{\lim \limits_{x\,\to\,+\infty}F(x) = 2}\) für \(x \to +\infty\) der waagrechte Asymptote mit der Gleichung \(\textcolor{#e9b509}{y = 2}\) annähert.
Die Skizze sollte zudem qualitativ zeigen, dass die Extremstellen von \(\boldsymbol{G_{f}}\) die Wendestellen von \(\textcolor{#e9b509}{G_{F}}\) sind.
Ausführliche Erklärung (nicht verlangt)
Verlauf von \(G_{F}\) an den Nullstellen von \(G_{f}\)
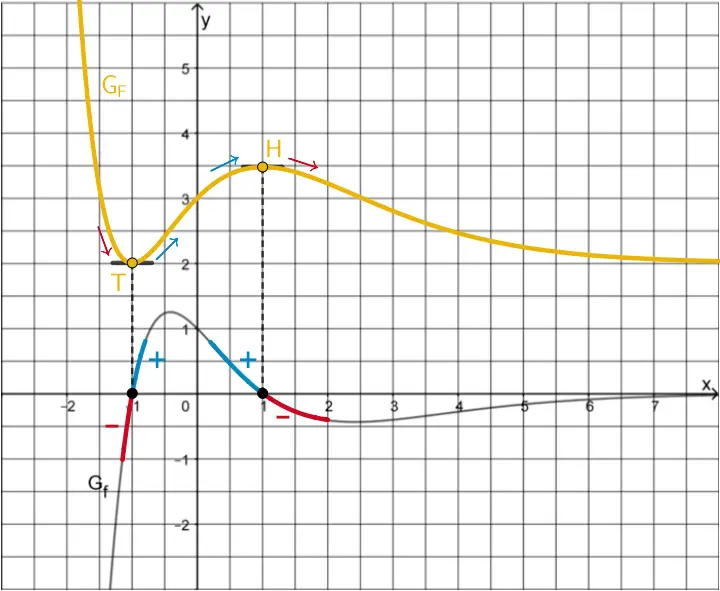
Betrachtung der Nullstelle \(x = -1\) von \(G_{f}\)
Aus Teilaufgabe 1d ist bekannt, dass \(\textcolor{#e9b509}{G_{F}}\) den Tiefpunkt \(\textcolor{#e9b509}{T(-1|2)}\) besitzt (Begründung vgl. Teilaufgabe 1d).
Betrachtung der Nullstelle \(x = 1\) von \(G_{f}\)
Gemäß der Definition einer Stammfunktion gilt \(F'(x) = f(x)\).
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
Mit \(f(1) = \boldsymbol{F'(1) = 0}\) bedeutet die Nullstelle \(x = 1\) von \(G_{f}\), dass der Graph der Stammfunktion \(\textcolor{#e9b509}{F}\) an der Stelle \(x = 1\) eine waagrechte Tangente hat.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Der Vorzeichenwechsel von \(\boldsymbol{G_{f}}\) an der Nullstelle \(\boldsymbol{x = 1}\) von \(\textcolor{#0087c1}{\textbf{+}}\) nach \(\textcolor{#cc071e}{\Large{\textbf{-}}}\) bedeutet nach dem Monotoniekriterium, dass der Graph der Stammfunktion \(\textcolor{#e9b509}{F}\) an der Stelle \(x = 1\) das Monotonieverhalten von streng monoton steigend \((\textcolor{#0087c1}{f(x) = F'(x) > 0})\) zu streng monoton fallend \((\textcolor{#cc071e}{f(x) = F'(x) < 0})\) wechselt.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Also ist der Punkt \(\textcolor{#e9b509}{H(1|(F(1))}\) mit \(\textcolor{#e9b509}{F(1) \approx 3{,}5}\) (vgl. Angabe) Hochpunkt des Graphen der Stammfunktion \(\textcolor{#e9b509}{F}\).
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[\left. \begin{align*} &\textcolor{#0087c1}{f(x) = F'(x) > 0} \enspace \text{für} \enspace x < 1 \\ &f(1) = F'(1) = 0 \\ &\textcolor{#cc071e}{f(x) = F'(x) < 0} \enspace \text{für} \enspace x > 1 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#e9b509}{\text{Hochpunkt} \; H\,(1|(F(1))}\]
Verlauf von \(G_{F}\) an den Extremstellen von \(G_{f}\)
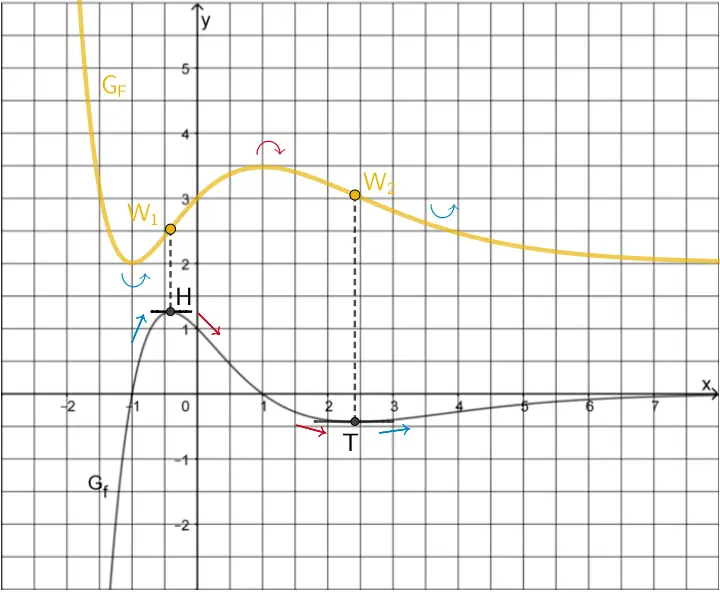
Die Extremstellen \(x \approx -0{,}4\) und \(x \approx 2{,}4\) von \(G_{f}\) sind Wendestellen von \(G_{F}\).
An den Extremstellen besitzt \(G_{f}\) je eine waagrechte Tangente. Das heißt, es gilt \(f'(-0{,}4) = \boldsymbol{F''(-0{,}4) \approx 0}\) bzw. \(f'(2{,}4) = \boldsymbol{F''(2{,}4) \approx 0}\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Im Hochpunkt \(\boldsymbol{H}\) wechselt \(\boldsymbol{G_{f}}\) das Monotonieverhalten von
streng Monoton steigend \((\textcolor{#0087c1}{f'(x) > 0})\) zu streng monoton fallend \((\textcolor{#cc071e}{f'(x) < 0})\)
und im Tiefpunkt \(\boldsymbol{T}\) wechselt \(\boldsymbol{G_{f}}\) das Monotonieverhalten von
streng monoton fallend \((\textcolor{#cc071e}{f'(x) < 0})\) zu streng monoton steigend \((\textcolor{#0087c1}{f'{x} > 0})\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Mit \(f'(x) = F''(x)\) bedeutet der Wechsel des Monotonieverhaltens von \(G_{f}\), dass der Graph der Stammfunktion \(\textcolor{#e9b509}{F}\) das Krümmungsverhalten von
linksgekrümmt \((\textcolor{#0087c1}{f'(x) = F''(x) > 0})\) zu rechtsgekrümmt \((\textcolor{#cc071e}{f'(x) = F''(x) < 0})\) bzw. von
rechtsgekrümmt \((\textcolor{#cc071e}{f'(x) = F''(x) < 0})\) zu linksgekrümmt \((\textcolor{#0087c1}{f'(x) = F''(x) > 0})\) wechselt.
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Also hat \(\textcolor{#e9b509}{G_{F}}\) an den Extremstellen von \(G_{f}\) je einen Wendepunkt.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*} &\textcolor{#0087c1}{f'(x) = F''(x) > 0} \enspace \text{für} \enspace x \lessapprox -0{,}4 \\ &f'(-0{,}4) = F''(-0{,}4) \approx 0 \\ &\textcolor{#cc071e}{f'(x) = F''(x) < 0} \enspace \text{für} \enspace x \gtrapprox -0{,}4 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#e9b509}{\text{Wendepunkt} \; W_{1}}\]
\[\left. \begin{align*} &\textcolor{#cc071e}{f'(x) = F''(x) < 0} \enspace \text{für} \enspace x \lessapprox 2{,}4 \\ &f'(2{,}4) = F''(2{,}4) \approx 0 \\ &\textcolor{#0087c1}{f'(x) = F''(x) > 0} \enspace \text{für} \enspace x \gtrapprox 2{,}4 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#e9b509}{\text{Wendepunkt} \; W_{2}}\]
Verlauf von \(G_{F}\) für \(x \to +\infty\)
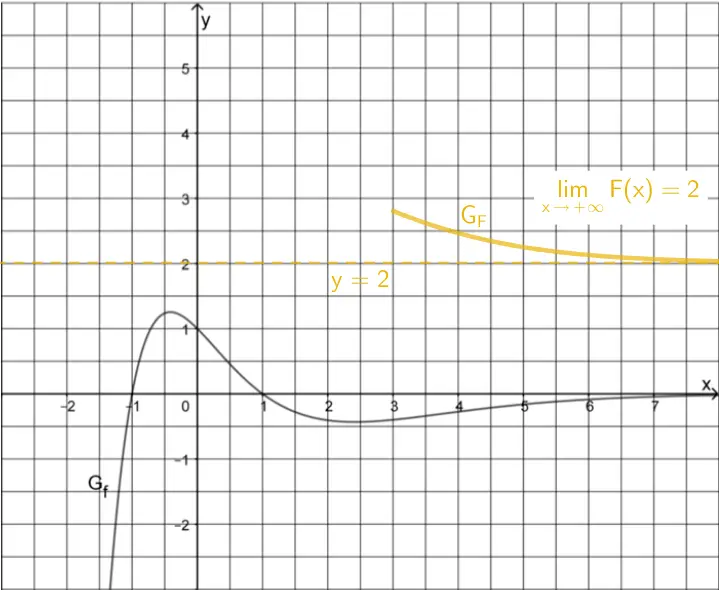
Es gilt \(\textcolor{#e9b509}{\lim \limits_{x\,\to\,+\infty}F(x) = 2}\) (vgl. Angabe). Das bedeutet, dass sich der Graph der Stammfunktion \(\textcolor{#e9b509}{F}\) für \(x \to +\infty\) der waagrechten Asymptote mit der Gleichung \(\textcolor{#e9b509}{y = 2}\) annähert.
Verlauf von \(G_{F}\) für \(x \to -\infty\)
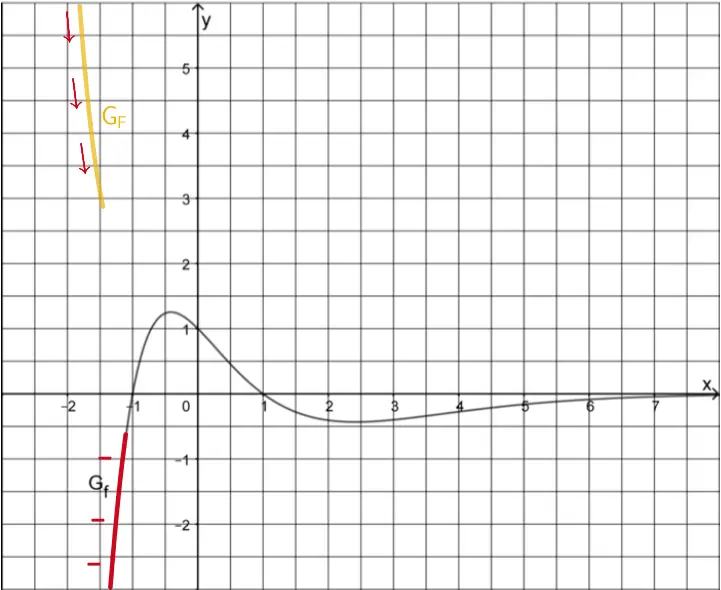
Für \(x \to -\infty\) strebt der Graph von \(G_{f}\) schnell gegen \(\textcolor{#cc071e}{-\infty}\). Mit \(f(x) = F'(x)\) folgt:
\[\lim \limits_{x\,\to\,-\infty}f(x) = \textcolor{#e9b509}{\lim \limits_{x\,\to\,-\infty}F'(x)} = \textcolor{#cc071e}{-\infty}\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Das bedeutet, dass die Steigung von \(\textcolor{#e9b509}{G_{F}}\) für \(x \to -\infty\) beliebig negativ wird, während \(\textcolor{#e9b509}{G_{F}}\) schnell gegen \(\textcolor{#e9b509}{+\infty}\) strebt.
Zusammenfassung
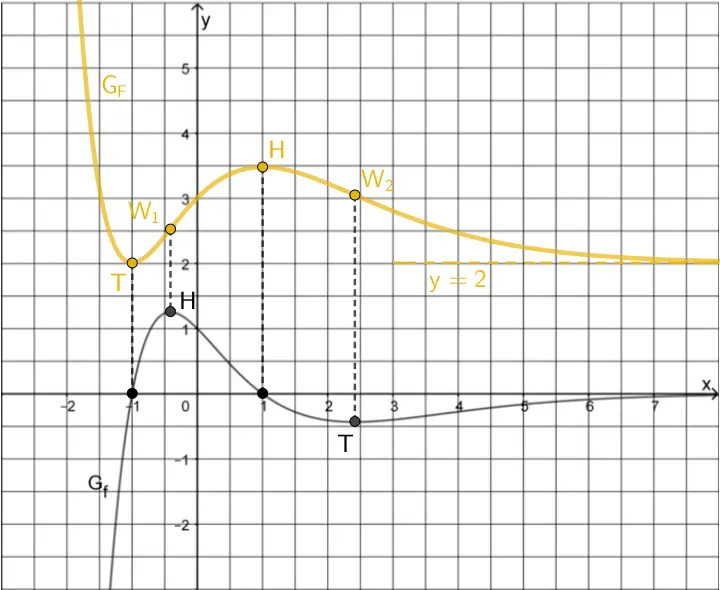
Graph der Stammfunktion \(\textcolor{#e9b509}{F}\) mit Extrem- und Wendepunkten sowie der waagrechten Asymptote mit der Gleichung \(\textcolor{#e9b509}{y = 2}\)

