Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.
\[f(x)= \ln(x + 3)\]
(2 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = \ln(x + 3)\]
Maximaler Definitionsbereich der Funktion \(f\)
Der Defiitionsbereich der Logarithmusfunktion, \(D = \mathbb R^+\), bestimmt den Definitionsbereich der Funktion \(f\,\).
\[\begin{align*} x + 3 &> 0 & &| -3 \\[0.8em] x &> -3 \end{align*}\]
\[\Longrightarrow \quad D_f = \; ]-3;\infty[\]
Term der Ableitungsfunktion von \(f\)
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[f(x) = \ln(x + 3) \quad \Longrightarrow \quad f'(x) = \frac{1}{x + 3} \cdot 1 = \frac{1}{x + 3}\]
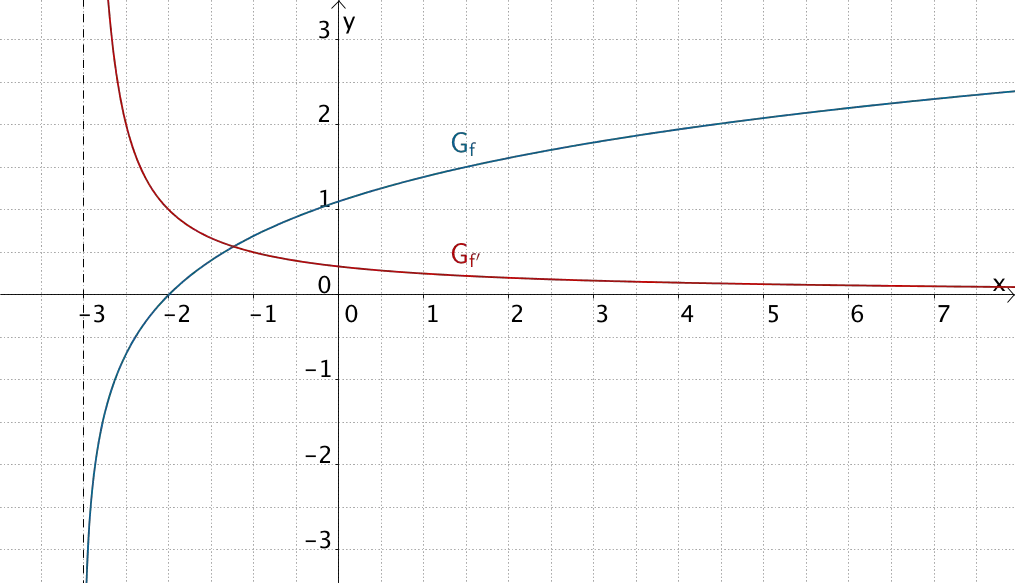
Verlauf des Graphen von \(f\) und des Graphen von \(f'\) mit \(D_f = \; ]-3;\infty[\)

