Auf dieser Flugbahn gibt es einen Punkt mit minimalem Abstand zur oberen Netztkante. Berechnen Sie diesen minimalen Abstand.
(3 BE)
Lösung zu Teilaufgabe 2b
Wie aus Teilaufgabe 2a bekannt ist, kann der in der Aufgabenstellung genannte Abstand mit \(d(x) = \sqrt{5x^2 - 1{,}8x + 0{,}2025}\) beschrieben werden.
Die notwendige Bedingung für eine Extremstelle von \(d\) lautet: \(d'(x) = 0\).
Extremstelle(n) bestimmen

Extremstelle(n) bestimmen mit Vorzeichenwechsel der 1. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#cc071e}{f'(x_0) = 0}\) ist und \(\textcolor{#cc071e}{f'}\) bei \(x_0\) einen Vorzeichenwechsel
von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{–}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
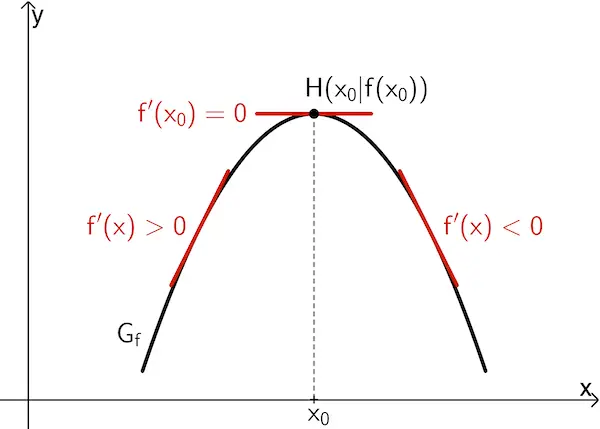
von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#cc071e}{+}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
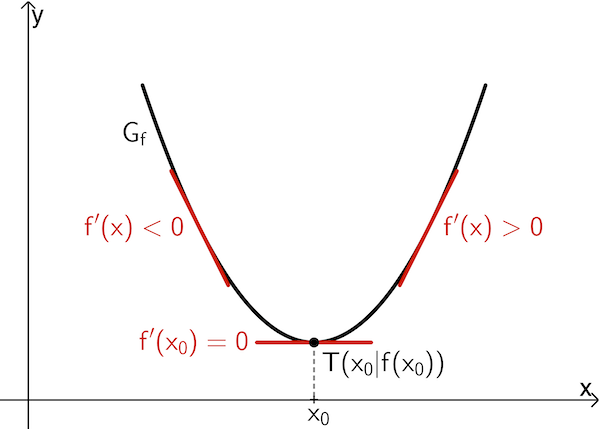
Extremstelle(n) bestimmen mit Vorzeichen der 2. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
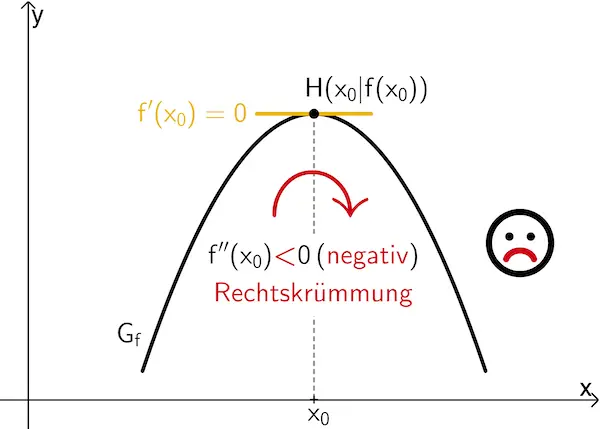
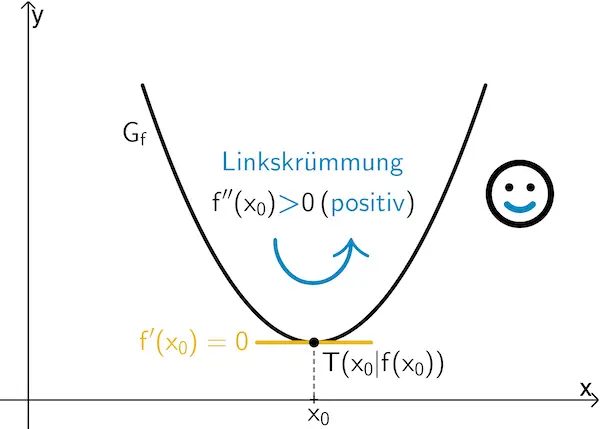
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
Da der Wert einer Wurzel minimal ist, wenn der Wert des Radikanden (Term unter der Wurzel) minimal ist, genügt es, den Radikanden \(5x^2 - 1{,}8x +0{,}2025\) abzuleiten.

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\left( 5x^2 - 1{,}8x +0{,}2025\right)' = 10x - 1{,}8\]
\[d'(x) = 0 \; \Rightarrow \; 10x - 1{,}8 = 0 \; \Leftrightarrow \; \textcolor{#e9b509}{x = 0{,}18}\]
Zum Vergleich:
Das Ableiten von \(d\) mithilfe der Kettenregel führt natürlich zum gleichen Ergebnis.
\[d(x) = \textcolor{#0087c1}{\sqrt{\textcolor{#cc071e}{5x^2 - 1{,}8x + 0{,}2025}}}\]
\[\begin{align*}d'(x) &= \textcolor{#0087c1}{\frac{1}{2\sqrt{\textcolor{#cc071e}{5x^2-1{,}8x+0{,}2025}}}} \cdot \textcolor{#cc071e}{10x -1{,}8} \\[0.8em] &= \frac{10x-1{,}8}{2\sqrt{5x^2-1{,}8x + 0{,}2025}}\end{align*}\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
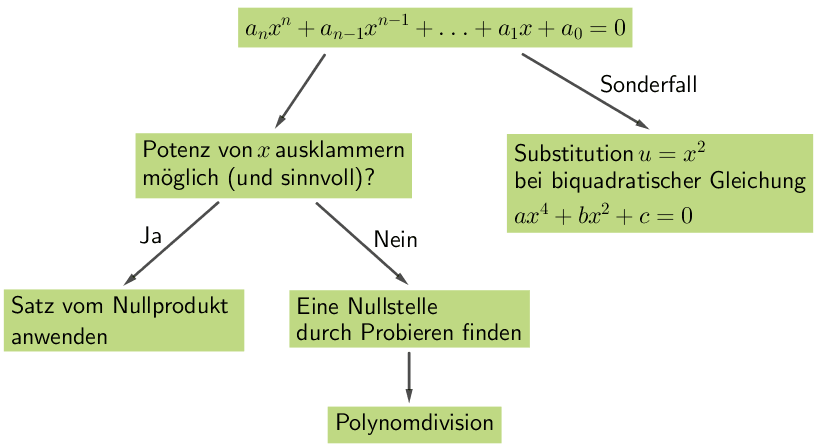
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
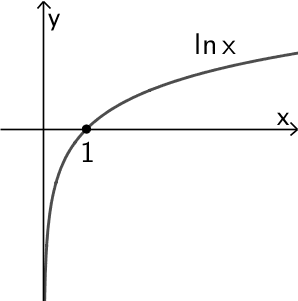
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
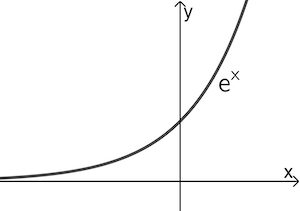
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[d'(x) = 0 \; \Rightarrow \; 10x - 1{,}8 = 0 \; \Leftrightarrow \; \textcolor{#e9b509}{x = 0{,}18}\]
Damit ist \(d(\textcolor{#e9b509}{0{,}18})\) der gesuchte minimale Abstand (vgl. Angabe).
\[d(\textcolor{#e9b509}{0{,}18}) = \sqrt{5 \cdot \textcolor{#e9b509}{0{,}18}^2 - 1{,}8 \cdot \textcolor{#e9b509}{0{,}18} + 0{,}2025} \approx 0{,}20\]
Der minimale Abstand der Flugbahn des Federballs zur oberen Netzkante beträgt etwa 20 cm.


