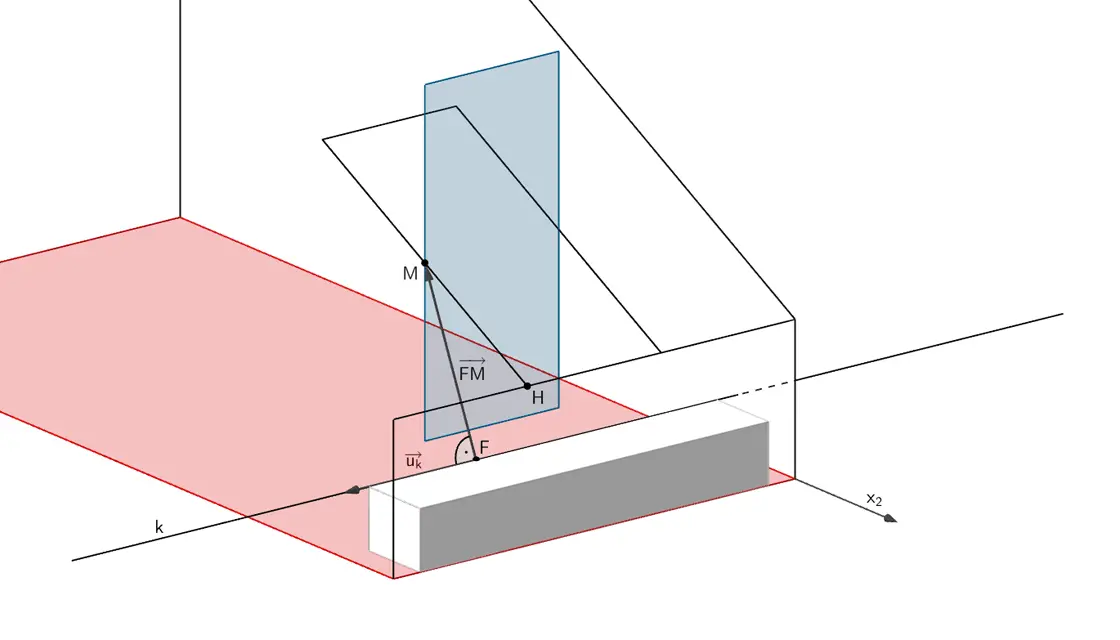
Überprüfen Sie rechnerisch, ob das Fenster bei seiner Drehung am Möbelstück anstoßen kann.
(5 BE)
Lösung zu Teilaufgabe g
1. Lösungsansatz mit Hilfsebene
2. Lösungsansatz: Anwenden des Skalarprodukts
3. Lösungsansatz: Anwenden der Differentialrechnung
4. Lösungsansatz: Betrachtung einer Projektion in die \(x_2x_3\)-Ebene
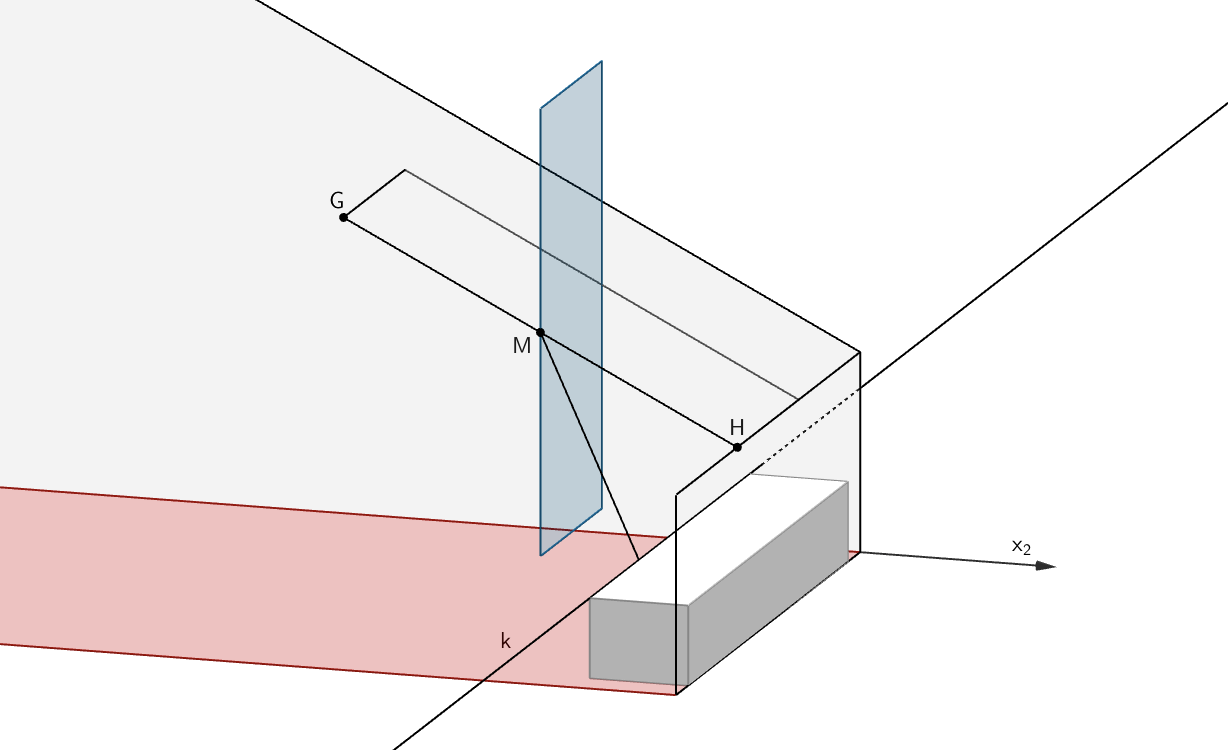
Damit das Fenster bei seiner Drehung nicht am Möbelstück anstößt, muss die Länge der Strecke \(\,[MH]\,\) kleiner sein als der Abstand \(\,d\,(M;k)\,\) des Punktes \(\,M\,\) von der Geraden \(\,k\,\).
Abstand eines Punktes von einer Geraden
\[M\,(2|5|1{,}5)\,, \qquad k \, \colon \enspace \overrightarrow{X} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\,, \quad \lambda \in \mathbb R\]
1. Lösungsansatz mit Hilfsebene
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
Hilfsebene \(Z\) mit den Eigenschaften \(M \in Z\) und \(Z \perp k\) bestimmen:
\[\overrightarrow{n}_Z = \overrightarrow{u}_k = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\]
\[Z \, \colon \enspace \overrightarrow {n}_Z \circ \left( \overrightarrow X - \overrightarrow M \right) = 0\]
\[Z \, \colon \; \begin {pmatrix} 1 \\ 0 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 2 \\ 5 \\ 1{,}5 \end {pmatrix} \right] = 0\]
Lage der Hilfsebene \(Z\)
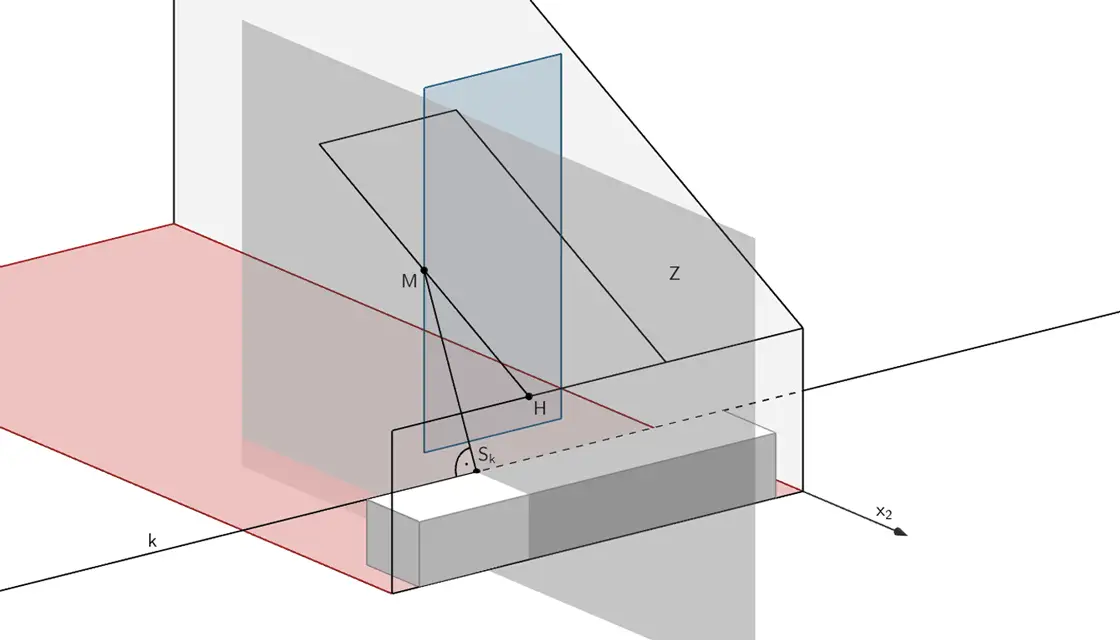
Schnittpunkt \(S_k\) der Geraden \(k\) mit der Hilfsebene \(Z\) ermitteln:
Zur Berechnung des Schnitpunktes \(S_k\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(k\) in die Normalengleichung der Hilfsebene \(Z\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[k \, \colon \enspace \overrightarrow{X} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\]
\[Z \, \colon \; \begin {pmatrix} 1 \\ 0 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 2 \\ 5 \\ 1{,}5 \end {pmatrix} \right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} k \cap Z \, \colon \enspace \begin {pmatrix} 1 \\ 0 \\ 0 \end {pmatrix} \circ \left[ \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - \begin {pmatrix} 2 \\ 5 \\ 1{,}5 \end {pmatrix} \right] &= 0 \\[0.8em] \begin {pmatrix} 1 \\ 0 \\ 0 \end {pmatrix} \circ \left[ \begin{pmatrix} -2 \\ 0{,}5 \\ -1{,}1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \right] &= 0 \\[0.8em] 1 \cdot (-2 + \lambda) + 0 \cdot 0{,}5 + 0 \cdot -1{,}1 &= 0 \\[0.8em] -2 + \lambda &= 0 & &| + 2 \\[0.8em] \lambda &= 2 \end{align*}\]
Parameterwert \(\lambda = 2\) in \(k\) einsetzen:
\[S_k \in k \, \colon \enspace \overrightarrow{S}_k = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 5{,}5 \\ 0{,}4 \end{pmatrix}\]
Länge der Strecke \([MS_k]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{MS_k} &= \vert \overrightarrow{MS_k} \vert \\[0.8em] &= \vert \overrightarrow{S}_k - \overrightarrow{M} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} - \begin{pmatrix} 2 \\ 5 \\ 1{,}5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0{,}5 \\ -1{,}1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 0{,}5^2 + 1{,}1^2} \\[0.8em] &= \sqrt{1{,}46} \approx 1{,}21 \end{align*}\]
\[\Longrightarrow \quad d\,(M;k) = d\,(M;S_k) \approx 1{,}21 \]
\(\displaystyle \overline{MH}= \frac{1}{2} \cdot \sqrt{5} \approx 1{,}12\;\) (siehe Teilaufgabe e)
\[\Longrightarrow \quad \overline{MH} < d\,(M;k)\]
\(\Longrightarrow \quad\) Das Fenster kann bei seiner Drehung nicht am Möbelstück anstoßen.
2. Lösungsansatz: Anwenden des Skalarprodukts
\[M\,(2|5|1{,}5)\,, \qquad k \, \colon \enspace \overrightarrow{X} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\,, \quad \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
Es sei \(\,F\,\) der Lotfußpunkt des Lotes des Punktes \(\,M\,\) auf die Gerade \(\,k\,\). Der Richtungsvektur \(\,\overrightarrow{u}_k\,\) der Geraden \(\,k\,\) und er Vektor \(\,\overrightarrow{FM}\,\) stehen senkrecht zueinander.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Somit gilt: \(\enspace \overrightarrow{FM} \perp \overrightarrow{u}_k \quad \Longrightarrow \quad \overrightarrow{FM} \circ \overrightarrow{u}_k = 0\)
Vektor \(\overrightarrow{FM}\) allgemein beschreiben:
\[F \in k\,\colon \enspace \overrightarrow{F} = \begin{pmatrix} \lambda \\ 5{,}5 \\ 0{,}4 \end{pmatrix}\]
\[\overrightarrow{FM} = \overrightarrow{M} - \overrightarrow{F} = \begin{pmatrix} 2 \\ 5 \\ 1{,}5 \end{pmatrix} - \begin{pmatrix} \lambda \\ 5{,}5 \\ 0{,}4 \end{pmatrix} = \begin{pmatrix} 2 - \lambda \\ -0{,}5 \\ 1{,}1 \end{pmatrix}\]
Koordinaten des Lotfußpunktes \(F\) bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{FM} \circ \overrightarrow{u}_k &= 0 \\[0.8em] \begin{pmatrix} 2 - \lambda \\ -0{,}5 \\ 1{,}1 \end{pmatrix} \circ \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} &= 0 \\[0.8em] (2 - \lambda) \cdot 1 + (-0{,}5) \cdot 0 + 1{,}1 \cdot 0 &= 0 \\[0.8em] 2 - \lambda &= 0 & &| + \lambda \\[0.8em] \lambda &= 2 \end{align*}\]
Parameterwert \(\lambda = 2\) in \(k\) einsetzen:
\[F \in k\,\colon \enspace \overrightarrow{F} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} \]
Länge der Strecke \([MF]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{MF} &= \vert \overrightarrow{MF} \vert \\[0.8em] &= \vert \overrightarrow{F} - \overrightarrow{M} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} - \begin{pmatrix} 2 \\ 5 \\ 1{,}5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0{,}5 \\ -1{,}1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 0{,}5^2 + 1{,}1^2} \\[0.8em] &= \sqrt{1{,}46} \approx 1{,}21 \end{align*}\]
\[\Longrightarrow \quad d\,(M;k) = d\,(M;F) \approx 1{,}21 \]
\(\displaystyle \overline{MH}= \frac{1}{2} \cdot \sqrt{5} \approx 1{,}12\;\) (siehe Teilaufgabe e)
\[\Longrightarrow \quad \overline{MH} < d\,(M;k)\]
\(\Longrightarrow \quad\) Das Fenster kann bei seiner Drehung nicht am Möbelstück anstoßen.
3. Lösungsansatz: Anwenden der Differentialrechnung
\[M\,(2|5|1{,}5)\,, \qquad k \, \colon \enspace \overrightarrow{X} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\,, \quad \lambda \in \mathbb R\]
Abstand Punkt - Gerade, Ansatz: Differentialrechnung anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
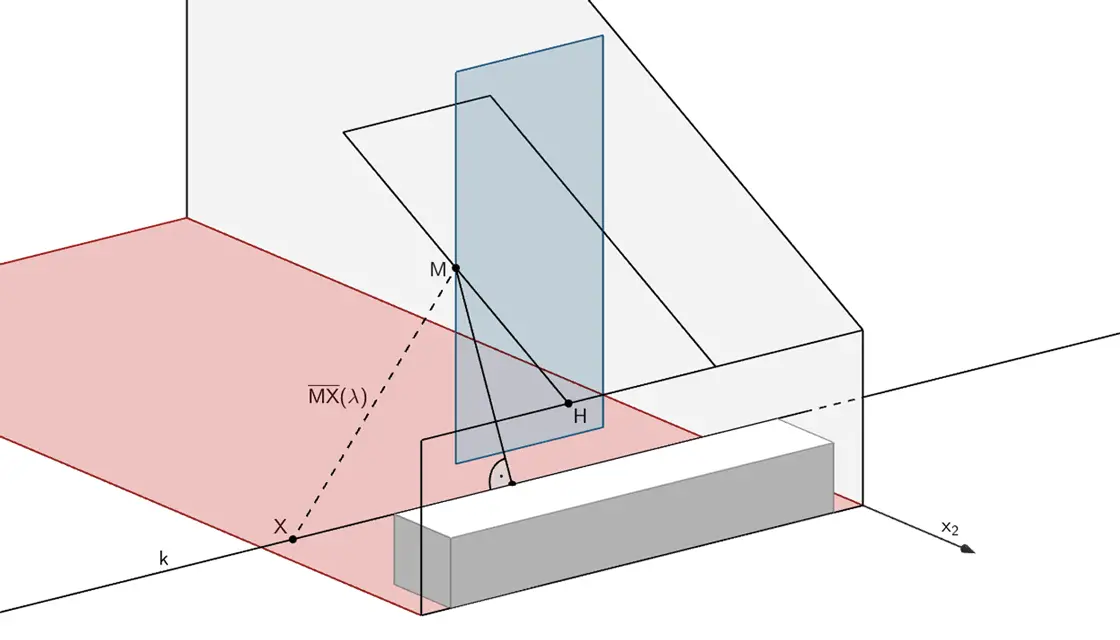
1. Länge der Strecke \([PX]\) zwischen dem Punkt \(P\) und einem beliebigen Punkt \(X \in g\) beschreiben:
\[\overline{PX} = \vert \overrightarrow X - \overrightarrow P \vert \quad \Longrightarrow \quad \overline{PX}(\lambda) = \vert \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \vert\]
2. Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\[\left. \begin{align*} &\overline{PX}^{\;\prime}(\lambda_{min}) \enspace = \enspace 0 \\ \\ &\overline{PX}^{\;\prime \prime}(\lambda_{min}) \; > \enspace 0 \end{align*} \right\} \quad \Longrightarrow \quad \lambda_{min} \]
3. Minimale Länge berechnen:
\[\overline{PX}(\lambda_{min}) = d\,(P;g)\]
Die Länge der Strecke \(\,[MX]\,\) zwischen dem Punkt \(\,M\,\) und einem beliebigen Punkt \(\,X \in k\,\) lässt sich in Abhängigkeit des Parameterwertes \(\,\lambda\,\) der Geradengleichung von \(\,k\,\) beschreiben.
Länge der Strecke \([MX]\) in Abhängigkeit von \(\lambda\,\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{MX} = \vert \overrightarrow{X} - \overrightarrow{M} \vert\]
\[\begin{align*} \overline{MX}(\lambda) &= \left| \begin{pmatrix} \lambda \\ 5{,}5 \\ 0{,}4 \end{pmatrix} - \begin{pmatrix} 2 \\ 5 \\ 1{,}5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} \lambda - 2 \\ 0{,}5 \\ -1{,}1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(\lambda - 2)^2 + 0{,}5^2 + (-1{,}1)^2} \\[0.8em] &= \sqrt{\lambda^2 - 4\lambda + 4 + 0{,}25 + 1{,}21} \\[0.8em] &= \sqrt{\lambda^2 - 4\lambda +5{,}46} \end{align*}\]
Parameterwert \(\lambda_{min}\) für minimale Länge bestimmen:
\(\overline{MX}(\lambda)\) ist minimal, wenn der Wert des Radikanden minimal ist.
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[\big( \lambda^2 - 4\lambda + 5{,}46 \big)' \overset{!}{=} 0\]
Erste Ableitung des Radikanden bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\big( \lambda^2 - 4\lambda + 5{,}46 \big)' = 2\lambda - 4\]
\[\begin{align*}\Longrightarrow \quad 2\lambda - 4 &= 0 & &| + 4 \\[0.8em] 2\lambda &= 4 & &| : 2 \\[0.8em] \lambda &= 2 \end{align*}\]
Art der Extremstelle:
\[\big( \lambda^2 - 4\lambda +5{,}46 \big)'' = (2\lambda - 4)' = 2\]
\[\Longrightarrow \quad \big( \lambda^2 - 4\lambda +5{,}46 \big)'' > 0 \]
\(\Longrightarrow \quad \overline{MX}(\lambda)\) ist für \(\lambda_{min} = 2\) minimal.
Minimale Länge berechnen:
\[d\,(M;k) = \overline{MX}(\lambda_{min}) = \sqrt{2^2 - 4 \cdot 2 + 5{,}46} = \sqrt{1{,}46} \approx 1{,}21\]
\(\displaystyle \overline{MH}= \frac{1}{2} \cdot \sqrt{5} \approx 1{,}12\;\) (siehe Teilaufgabe e)
\[\Longrightarrow \quad \overline{MH} < d\,(M;k)\]
\(\Longrightarrow \quad\) Das Fenster kann bei seiner Drehung nicht am Möbelstück anstoßen.
4. Lösungsansatz: Betrachtung einer Projektion in die \(x_2x_3\)-Ebene
\[M\,(2|5|1{,}5)\,, \qquad k \, \colon \enspace \overrightarrow{X} = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\,, \quad \lambda \in \mathbb R\]
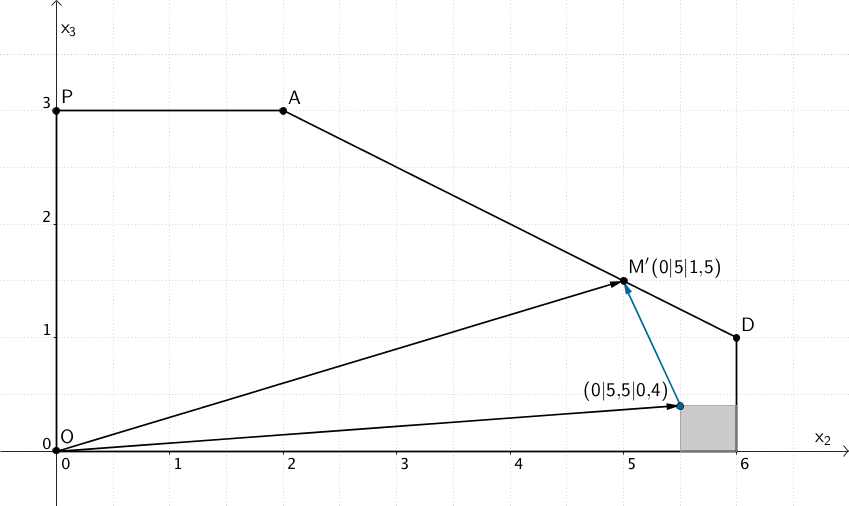
Der Aufpunkt \((0|5{,}5|0{,}4)\) der Geraden \(k\) liegt in der \(x_2x_3\)-Ebene.
Es sei \(M'\) die Projektion des Punktes \(M\) in die \(x_2x_3\)-Ebene.
\[\Longrightarrow \quad M'\,(0|5|1{,}5)\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}d\,(M;k) &= \left| \begin{pmatrix} 0 \\ 5 \\ 1{,}5 \end{pmatrix} - \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -0{,}5 \\ 1{,}1 \end{pmatrix}\right| \\[0.8em] &= \sqrt{0^2 + (-0{,}5)^2 + 1{,}1^2} \\[0.8em] &= \sqrt{1{,}46} \approx 1{,}21 \end{align*}\]
\(\displaystyle \overline{MH}= \frac{1}{2} \cdot \sqrt{5} \approx 1{,}12\;\) (siehe Teilaufgabe e)
\[\Longrightarrow \quad \overline{MH} < d\,(M;k)\]
\(\Longrightarrow \quad\) Das Fenster kann bei seiner Drehung nicht am Möbelstück anstoßen.