Die Funktion \(F\) ist die in \(\mathbb R\) definierte Stammfunktion von \(f\) mit \(F(3) = 0\).
Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von \(F\) an der Stelle \(x = 2\) an.
(1 BE)
Lösung zu Teilaufgabe 5b
Stammfunktion
Stammfunktion
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
Gemäß der Definition einer Stammfunktion gilt:
\[F'(2) = f(2)\]
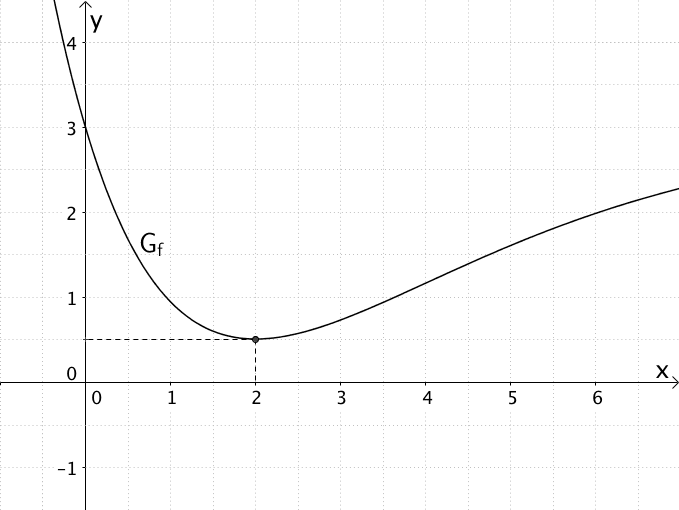
Der Abbildung entnimmt man den Näherungswert \(f(2) \approx 0{,}5\).
\[\Longrightarrow \quad F'(2) \approx 0{,}5\]
