Betrachtet wird die in \(\mathbb R\) definierte Funktion \(p \colon x \mapsto \dfrac{40}{(x - 12)^{2} + 4}\); die Abbildung zeigt den Graphen \(G_{p}\) von \(p\).
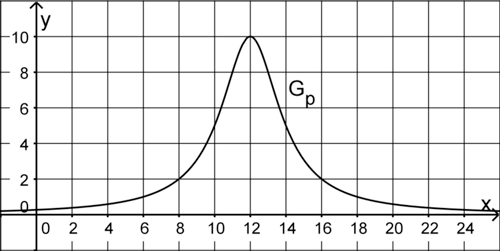
Beschreiben Sie, wie \(G_{p}\) aus dem Graphen der in \(\mathbb R\) definierten Funktion \(h \colon x \mapsto \dfrac{5}{x^{2} + 4}\) schrittweise hervorgeht, und begründen Sie damit, dass \(G_{p}\) bezüglich der Geraden mit der Gleichung \(x = 12\) symmetrisch ist.
(4 BE)
Lösung zu Teilaufgabe 3a
Beschreibung, wie \(G_{p}\) schrittweise aus dem Graphen von \(h\) hervorgeht
\[p(x) = \frac{40}{(x - 12)^{2} + 4} = \textbf{8} \cdot \frac{5}{(x - \textbf{12})^{2} + 4}; D_{p} = \mathbb R\]
\[h(x) = \frac{5}{x^{2} + 4}; \; D_{h} = \mathbb R\]
1. Streckung des Graphen von \(h\) in y-Richtung um den Faktor 8
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[\Rightarrow \enspace x \mapsto \textbf{8} \cdot \frac{5}{x^{2} + 4}\]
2. Verschiebung um 12 LE (Längeneinheiten) in positive x-Richtung
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Rightarrow \enspace p(x) = 8 \cdot \frac{5}{(x - \textbf{12})^{2} + 4} = \frac{40}{(x - 12)^{2} + 4}\]
Begründung, weshalb \(G_{p}\) bezüglich der Geraden mit der Gleichung \(x = 12\) symmetrisch ist
Zunächst ist zu zeigen, dass der Graph von \(h\) symmetrisch bezüglich der \(y\)-Achse ist.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
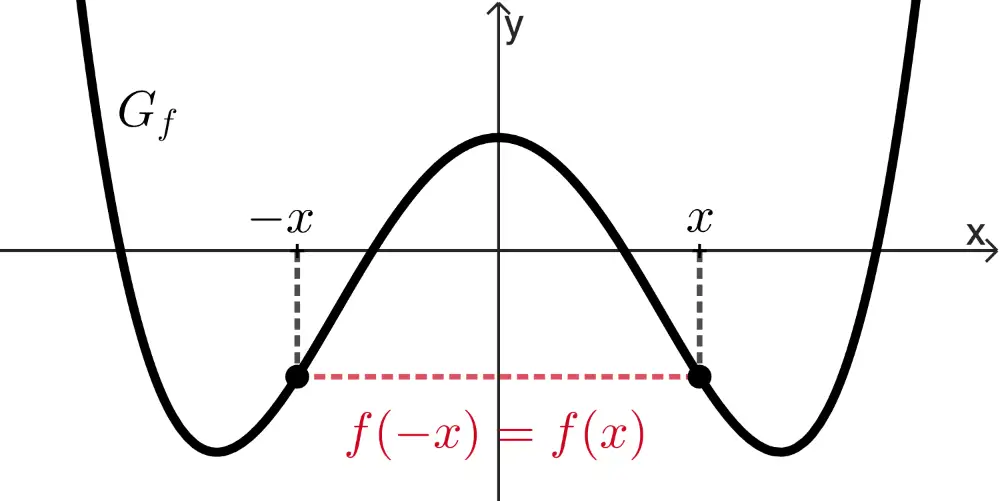
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
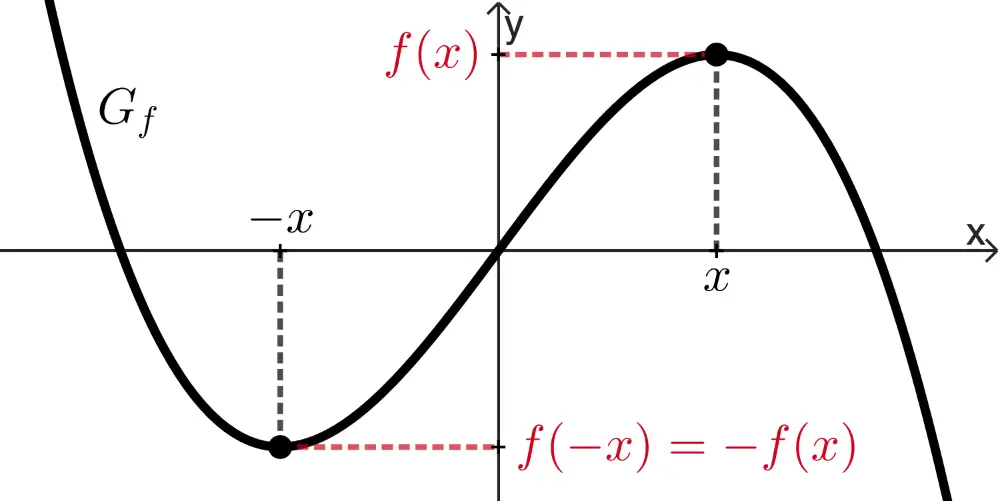
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[h(-x) = \frac{5}{(-x)^{2} + 4} = \frac{5}{x^{2} + 4} = h(x)\]
\(\Rightarrow\) Der Graph der Funktion \(\boldsymbol{h}\) ist symmetrisch bezüglich der \(\boldsymbol{y}\)-Achse.
Alternativer Nachweis des Symmetrieverhaltens des Graphen von \(h\):
\(h(x) = \dfrac{\textcolor{#0087c1}{5}}{x^{2} + \textcolor{#e9b509}{4}} = f_{\textcolor{#cc071e}{0},\textcolor{#0087c1}{5},\textcolor{#e9b509}{4}}(x)\) (vgl. Aufgbe 2)
Die Funktion \(h\) entspricht der Scharfunktion \(f_{\textcolor{#cc071e}{0},\textcolor{#0087c1}{5},\textcolor{#e9b509}{4}}\) mit \(\textcolor{#cc071e}{a = 0}\), \(\textcolor{#0087c1}{b = 5}\) und \(\textcolor{#e9b509}{c = 4}\) aus Aufgabe 2.
Aus der Angabe zu Teilaufgabe 2b ist bekannt, dass die Graphen der Funktionenschar \(f_{\textcolor{#cc071e}{a},\textcolor{#0087c1}{b},\textcolor{#e9b509}{c}}\) symmetrisch bezüglich der \(y\)-Achse sind, wenn \(\textcolor{#cc071e}{a = 0}\) und \(\textcolor{#0087c1}{b \neq 0}\) gilt.
Folglich ist der Graph der Funktion \(\boldsymbol{h}\) symmetrisch bezüglich der \(\boldsymbol{y}\)-Achse.
Schlussfolgerung
Da \(G_{p}\) gegenüber dem Graphen von \(h\) um 12 LE (Längeneinheiten) in positive x-Richtung verschoben ist (vgl. oben), ist \(G_{p}\) symmetrisch bezüglich der Geraden mit der Gleichung \(x = 12\). Die Streckung in y-Richtung wirkt sich nicht auf das Symmetrieverhalten von \(G_{p}\) aus.

