Eine in \(\mathbb R\) definierte ganzrationale, nicht lineare Funktion \(f\) mit erster Ableitungsfunktion \(f'\) und zweiter Ableitungsfunktion \(f''\) hat folgende Eigenschaften:
- \(f\) hat bei \(x_1\) eine Nullstelle.
- Es gilt \(f'(x_2) = 0\) und \(f''(x_2) \neq 0\).
- \(f'\) hat ein lokales Minimum an der Stelle \(x_3\).
Abbildung 1 zeigt die Positionen von \(x_1\), \(x_2\) und \(x_3\).
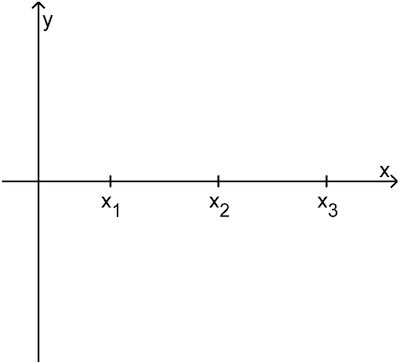 Abb. 1
Abb. 1
Begründen Sie, dass der Grad von \(f\) mindestens 3 ist.
(2 BE)
Lösung zu Teilaufgabe 3a
Begründung mithilfe der Eigenschaft:
- \(f'\) hat ein lokales Minimum an der Stelle \(x_3\).
Die Angabe schließt eine lineare Funktion (Grad 1) für \(f\) aus. Wäre \(f\) eine ganzrationale Funktion vom Grad 2, wäre deren erste Ableitungsfunktion \(f'\) vom Grad 1 und könnte kein lokales Minimum an der Stelle \(x_3\) haben (vgl. Angabe). Folglich muss der Grad von \(f\) mindestens 3 sein.
Alternative Formulierung:
Da \(f'\) an der Stelle \(x_3\) ein lokales Minimum hat, ist \(x_3\) eine Wendestelle des Graphen von \(f\). Somit gilt \(f''(x_3) = 0\) und dafür muss die zweite Ableitungsfunktion \(f''\) mindestens eine lineare Funktion (Grad 1) sein. Folglich ist der Grad der ersten Ableitungsfunktion \(f'\) mindestens 2 und der Grad der ganzrationalen Funktion \(f\) mindestens 3.
(vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte)


