Aufgabe 6
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{2x^2 - 8}{x^2 + x}\) mit maximaler Definitionsmenge \(D_f\).
- Bestimmen Sie \(D_f\) sowie die Nullstelle(n) von \(f\) und geben Sie die Gleichung(en) der senkrechten Asymptote(n) des Graphen von \(f\) an.
- Begründen Sie, dass \(y = 2\) die Gleichung der waagerechten Asymptote des Graphen von \(f\) ist.
a) Maximale Definitionsmenge, Nullstelle(n), senkrechte Asymptote(n)
Zunächst wird der Funktionsterm von \(f\) vollständig faktorisiert.
\[f(x) = \frac{2x^2 - 8}{x^2 + x} = \frac{2 \cdot (x^2 - 4)}{x \cdot (x+1)} = \frac{2 \cdot (x-2) \cdot (x+2)}{x \cdot (x+1)}\]
Am faktorisierten Funktionsterm ist zu erkennen, dass sich keiner der Faktoren kürzen lässt.
Maximale Definitionsmenge \(\boldsymbol{D_f}\)
An den Nullstellen des Nenners \(x \cdot (x+1)\) ist die gebrochenrationale Funktion \(f\) nicht definiert (Definitionslücken).
Maximale Definitionsmenge bestimmen
Gebrochenrationale Funktion / Quotient von Funktionen
\[x \mapsto \dfrac{Zähler(x)}{\textcolor{#e9b509}{\underbrace{Nenner(x)}_{\Large{\neq \, 0}}}}\]
Nullstelle(n) des Nenners ausschließen!
Wurzelfunktion
\[x \mapsto \sqrt{\mathstrut\smash{\textcolor{#e9b509}{\underbrace{\dots}_{\Large{\geq\,0}}}}} \\ {}\]
Der Wert des Terms unter der Wurzel (Radikand ) darf nicht negativ sein!
(natürliche) Logarithmusfunktion
\(x \mapsto \ln{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\) bzw. \(x \mapsto \log_{a}{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\)
Die (Natürliche) Logarithmusfunktion ist in \(\textcolor{#e9b509}{\mathbb R^{+}}\) definiert!
\[x \cdot (x + 1) = 0\; \Rightarrow \; x = -1, \; x = 0 \; \Rightarrow \; D_f = \mathbb R \backslash \{-1;0\}\]
Nullstelle(n) von \(\boldsymbol{f}\)
Die Nullstellen des Zählers \(2 \cdot (x-2) \cdot (x+2)\) sind die Nullstellen von \(f\).
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
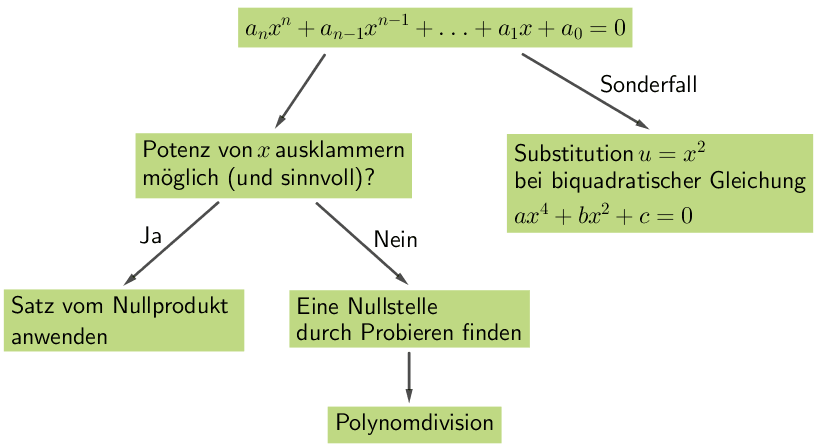
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
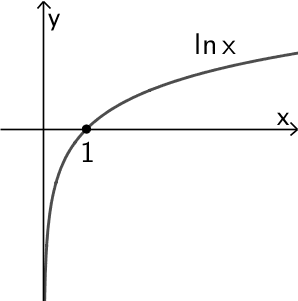
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
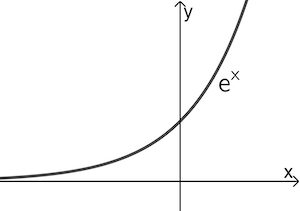
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[2 \cdot (x-2) \cdot (x+2) \; \Rightarrow \; x = -2, \; x = 2\]
Gleichungen der senkrechten Asymptoten des Graphen von \(\boldsymbol{f}\)
\(x = -1\) und \(x = 0\) (\(y\)-Achse)
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{p(x)}{q(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(p(x)\) und \(q(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(q(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Ergänzende Erklärung (nicht verlangt)
Die Nullstellen \(x = -1\) und \(x = 0\) des Nenners von \(f\) (Definitionslücken) sind nicht zugleich Nullstellen des Zählers von \(f\) und somit Polstellen. In der Umgebung dieser Polstellen verläuft der Graph von \(f\) steil nach \(-\infty\) bzw. \(+\infty\), indem er sich der senkrechten Geraden mit der Gleichung \(x = -1\) bzw. \(x = 0\) beliebig annähert (asymptotischer Verlauf).
b) Begründung, dass \(y=2\) die Gleichung der waagrechten Asymptote des Graphen von \(f\) ist
Begründung durch Vergleich der Grade des Zähler- und Nennerpolynoms
\[f(x) = \frac{\textcolor{#cc071e}{2}x^2 - 8}{\textcolor{#0087c1}{1}x^2 + x}\]
Da das Zähler- und das Nennerpolynom vom gleichen Grad sind, besitzt die gebrochenrationale Funktion \(f\) eine waagrechte Asymptote mit der Gleichung \(y = c\) mit \(c \in \mathbb R \backslash \{0\}\). Der Wert von \(c\) ergibt sich durch den Quotienten der Leitkoeffizienten der Polynome (Faktoren der höchsten Potenzen).
Gleichung der waagrechten Asymptote: \(y = \dfrac{\textcolor{#cc071e}{2}}{\textcolor{#0087c1}{1}} = 2\)
Begründung durch Grenzwertbetrachtung
Waagrechte (und schräge) Asymptoten beschreiben das Verhalten im Unendlichen des Graphen einer gebrochenrationalen Funktion.
Für eine aussagekräftige Grenzwertbetrachtung wird die höchste Potenz im Zähler und im Nenner ausgeklammert und gekürzt.
\[\begin{align*}\lim \limits_{x \to \pm \infty} f(x) &= \lim \limits_{x \to \pm \infty} \frac{\textcolor{#cc071e}{2}\textcolor{#e9b509}{x^2} - 8}{\textcolor{#0087c1}{1}\textcolor{#e9b509}{x^2} + x} &&| \; \textcolor{#e9b509}{x^2}\; \text{ausklammern und kürzen} \\[0.8em] &= \lim \limits_{x \to \pm \infty} \frac{\cancel{\textcolor{#e9b509}{x^2}} \cdot \big( \textcolor{#cc071e}{2} + \overset{\to\,0}{\frac{8}{x^2}} \big)}{\cancel{\textcolor{#e9b509}{x^2}} \cdot \big(\textcolor{#0087c1}{1} + \underset{\to\,0}{\frac{1}{x}}\big)} \\[0.8em] &= \frac{\textcolor{#cc071e}{2}}{\textcolor{#0087c1}{1}} = 2\end{align*}\]
Folglich ist \(y = 2\) die Gleichung der waagrechten Asymptote des Graphen von \(f\).
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.2 Gebrochenrationale Funktion)


