Abbildung 2 legt die Vermutung nahe, dass \(G_f\) bezüglich des Schnittpunkts \(P\,(-1|-1)\) seiner Asymptoten symmetrisch ist. Zum Nachweis dieser Symmetrie von \(G_f\) kann die Funktion \(g\) betrachtet werden, deren Graph aus \(G_f\) durch Verschiebung um 1 in positive \(x\)-Richtung und um 1 in positive \(y\)-Richtung hervorgeht.
Bestimmen Sie einen Funktionsterm von \(g\). Weisen Sie anschließend die Punktsymmetrie von \(G_f\) nach, indem Sie zeigen, dass der Graph von \(g\) punktsymmetrisch bezüglich des Koordinatenursprungs ist.
(Teilergebnis: \(\displaystyle g(x) = \frac{1}{2}x + \frac{8}{x}\))
(6 BE)
Lösung zu Teilaufgabe 2a
\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad D = \mathbb R \, \backslash \, \{-1\}\]
Funktionsterm von \(g\)
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\begin{align*} g(x) &= f(x - 1) + 1 \\[0.8em] &= \frac{1}{2} \cdot (x - 1) - \frac{1}{2} + \frac{8}{x - 1 + 1} + 1 \\[0.8em] &= \frac{1}{2}x - \frac{1}{2} - \frac{1}{2} + \frac{8}{x} + 1 \\[0.8em] &= \frac{1}{2}x + \frac{8}{x} \end{align*}\]
Nachweis der Punktsymmetrie von \(G_g\) und damit von \(G_f\)
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
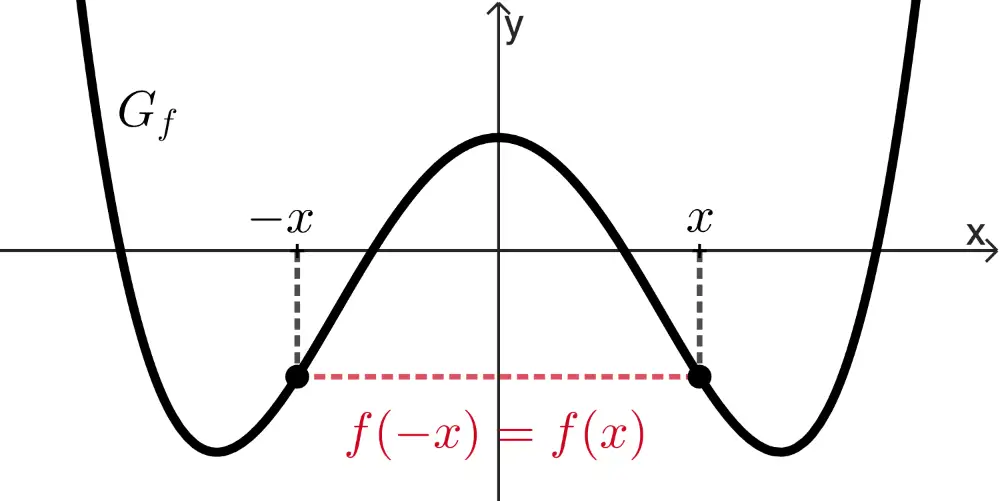
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
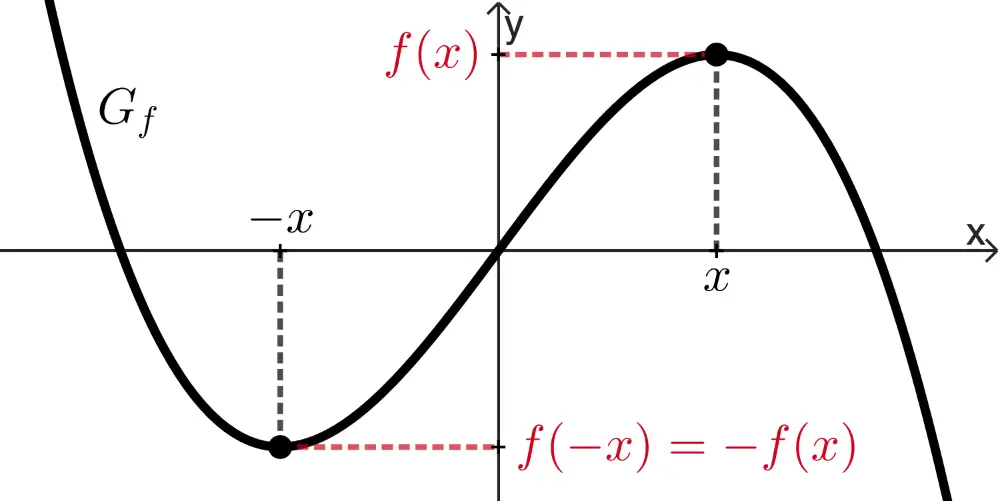
\[g(x) = \frac{1}{2}x + \frac{8}{x}\,; \quad D = \mathbb R\]
\[g(-x) = -\frac{1}{2}x - \frac{8}{x} = - \left(\frac{1}{2}x + \frac{8}{x}\right) = -g(x)\]
\(\Longrightarrow \quad G_g\) ist punktsymmetrisch zum Ursprung.
\(\Longrightarrow \quad G_f\) ist punktsymmetrisch zum Punkt \(P\,(-1|-1)\).
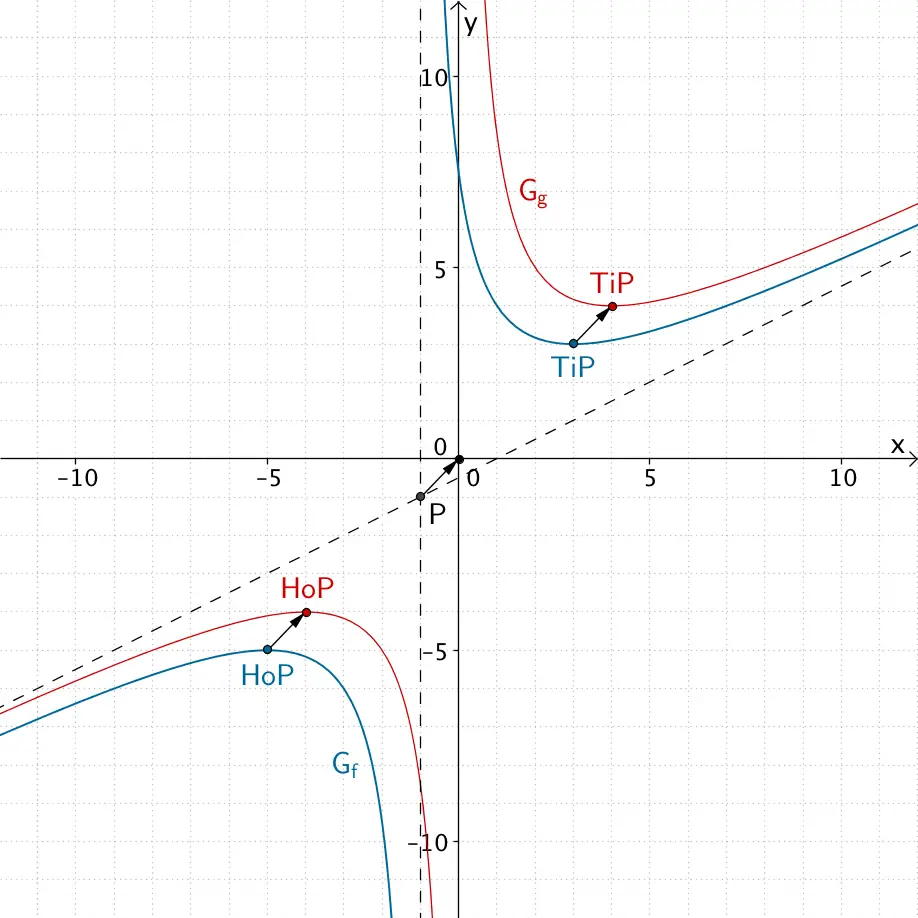
Der Graph von \(g\) geht aus dem Graphen von \(f\) durch Verschiebung um 1 in positive \(x\)-Richtung und um 1 in positive \(y\)-Richtung hervor. \(G_f\) ist punktsymmetrisch zum Punkt \(P\,(-1|-1)\) und \(G_g\) ist punktsymmetrisch zum Koordinatenursprung.

