- Details
- Kategorie: Geometrie 2
Abbildung 1 zeigt die Pyramide \(ABCDS\) mit den Eckpunkten \(A(-3|-3|0)\), \(B(3|-3|0)\), \(C(3|3|0)\), \(D(-3|3|0)\) und \(S(0|0|4)\) sowie den Punkt \(O(0|0|0)\), der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche \(CDS\) der Pyramide liegt in der Ebene \(E\).
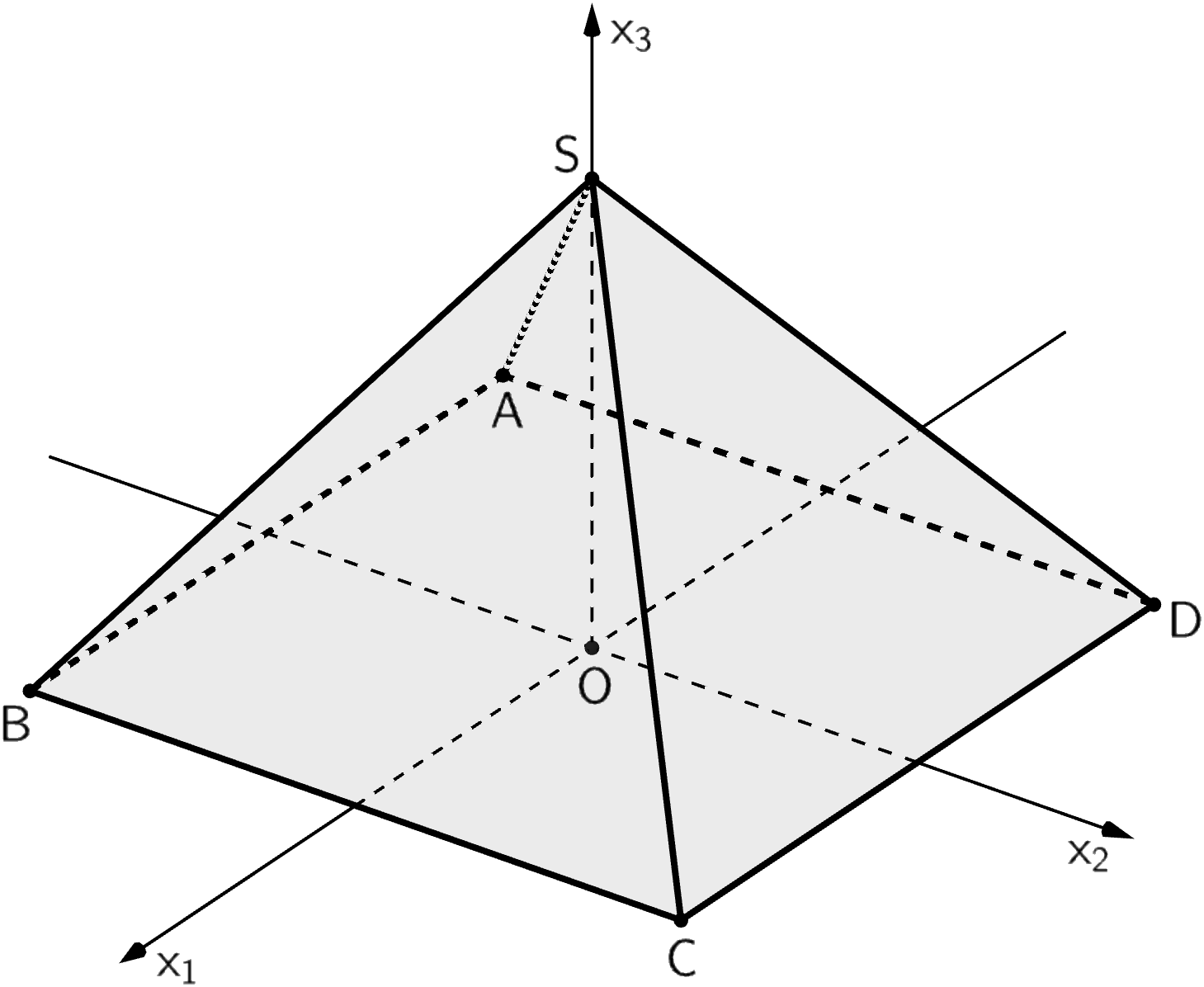Abb. 1
Berechnen Sie den Inhalt der Oberfläche der Pyramide.
(4 BE)
- Details
- Kategorie: Geometrie 2
Genau eine der folgenden Gleichungen (1) bis (3) beschreibt eine Symmetrieebene der Pyramide. Geben Sie diese Gleichung an und begründen Sie für eine der anderen Gleichungen, dass die durch sie beschriebene Ebene keine Symmetrieebene der Pyramide ist.
\[\textsf{(1)} \quad x_1-x_3=0\]
\[\textsf{(2)} \quad x_1+x_2+x_3=4\]
\[\textsf{(3)} \quad x_1+x_2= 0\]
(3 BE)
- Details
- Kategorie: Geometrie 2
Bestimmen Sie eine Gleichung von \(E\) in Koordinatenform.
(zur Kontrolle: \(4x_2+3x_3-12=0\))
(3 BE)
- Details
- Kategorie: Geometrie 2
Es gibt einen Punkt \(P(0|0|p)\), der im Inneren der Pyramide liegt und von allen vier Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe des folgenden Gleichungssystems lässt sich der Wert von \(p\) bestimmen:
\[\textsf{I} \quad \overrightarrow{Q} = \begin{pmatrix} 0\\0\\p \end{pmatrix}+ t \cdot \begin{pmatrix} 0\\4\\3 \end{pmatrix}\]
\[\textsf{II} \quad 4 \cdot 4t + 3 \cdot (p+3t) -12 = 0 \vphantom{\begin{pmatrix} 0\\0\\p \end{pmatrix}}\]
\[\textsf{III} \quad \vert \overrightarrow{PQ} \vert = p \vphantom{\begin{pmatrix} 0\\0\\p \end{pmatrix}}\]
Erläutern Sie die Überlegungen im geometrischen Zusammenhang, die diesem Vorgang zur Bestimmung des Werts von \(p\) zugrunde liegen.
(5 BE)
- Details
- Kategorie: Geometrie 2
Die Ebene \(E\) gehört zur Schar der Ebenen \(E_k \colon 4k \cdot x_1 + 4\sqrt{1-k^2} \cdot x_2 + 3 \cdot x_3 - 12 = 0\) mit \(k \in [-1;1]\).
Die Seitenfläche \(ADS\) der Pyramide liegt in der Ebene \(E_{-1}\) der Schar, die Seitenfläche \(BCS\) in der Ebene \(E_1\).
Zeigen Sie, dass der Punkt \(S\) in allen Ebenen der Schar enthalten ist.
(1 BE)
- Details
- Kategorie: Geometrie 2
Weisen Sie nach, dass die Größe des Winkels, unter dem die Gerade \(OS\) die Ebene \(E_k\) schneidet, unabhängig von \(k\) ist.
(4 BE)
- Details
- Kategorie: Geometrie 2
Jede Ebene \(E_k\) der Schar schneidet die \(x_1x_2\)-Ebene in einer Gerade \(g_k\). Mit \(R_k\) wird jeweils derjenige Punkt auf \(g_k\) bezeichnet, der von \(O\) den kleinsten Abstand hat. In Abbildung 2 sind \(g_k\) und \(R_k\) beispielhaft für eine Ebene \(E_k\) der Schar dargestellt.
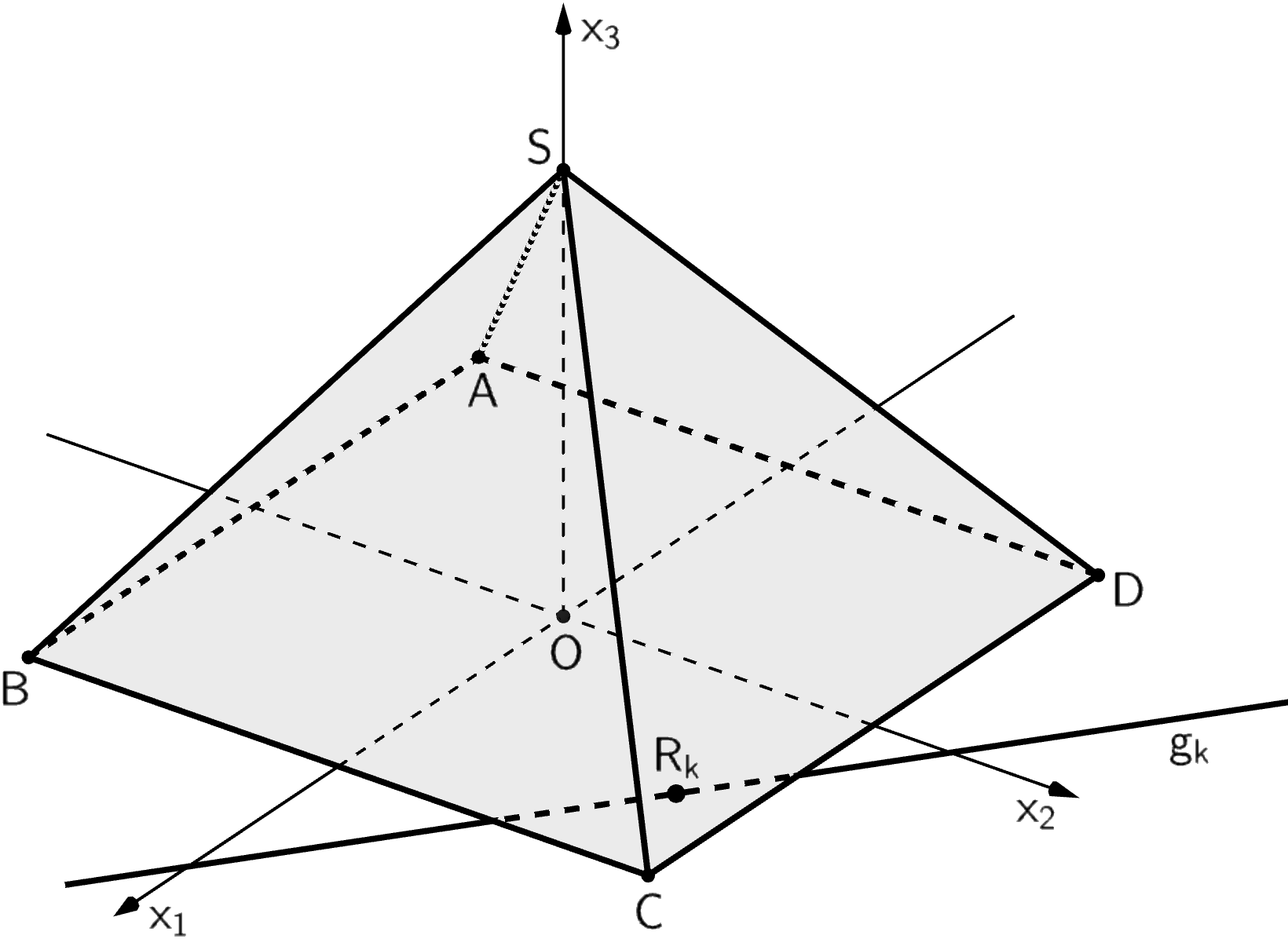Abb. 2
Zeichnen Sie die Punkte \(R_{-1}\) und \(R_1\) in Abbildung 2 ein.
(2 BE)
- Details
- Kategorie: Geometrie 2
Durchläuft \(k\) alle Werte von \(-1\) bis \(1\), dann dreht sich das Dreieck \(OR_kS\) um die Strecke \([OS]\). Dabei entsteht ein Körper. Beschreiben Sie die Form des entstehenden Körpers und bestimmen Sie das Volumen dieses Körpers.
(3 BE)
