Lotfußpunktverfahren

Die Kugel \(K\) mit dem Mittelpunkt \(M(-13|20|0)\) berührt die Ebene \(E\). Bestimmen Sie die Koordinaten des zugehörigen Berührpunkts \(F\) sowie den Kugelradius \(r\).

(zur Kontrolle: \(F(-5|4|2)\), \(r = 18\))

(6 BE)

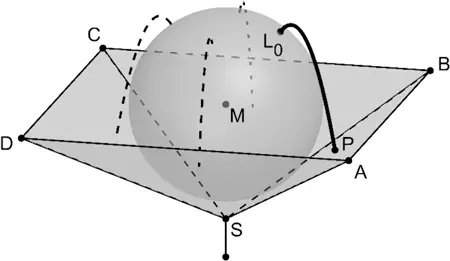
Ein auf einer Stange montierter Brunnen besteht aus einer Marmorkugel, die in einer Bronzeschale liegt. Die Marmorkugel berührt die vier Innenwände der Bronzeschale an jeweils genau einer Stelle. Die Bronzeschale wird im Modell durch die Seitenflächen der Pyramide \(ABCDS\) beschrieben, die Marmorkugel durch eine Kugel mit Mittelpunkt \(M(0|0|4)\) und Radius \(r\). Die \(x_{1}x_{2}\)-Ebene des Koordinatensystems stellt im Modell den horizontal verlaufenden Erdboden dar; eine Längeneinheit entspricht einem Dezimeter in der Realität.

Ermitteln Sie den Durchmesser der Marmorkugel auf Zentimeter genau.

(zur Kontrolle: \(r = \sqrt{6}\))

(4 BE)

Untersuchen Sie, ob \(K\) die \(x_1x_2\)-Ebene schneidet.

(2 BE)

Es gibt einen Punkt \(P(0|0|p)\), der im Inneren der Pyramide liegt und von allen vier Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe des folgenden Gleichungssystems lässt sich der Wert von \(p\) bestimmen:

Erläutern Sie die Überlegungen im geometrischen Zusammenhang, die diesem Vorgang zur Bestimmung des Werts von \(p\) zugrunde liegen.

(5 BE)