Begründen Sie, dass das Viereck \(ABA'B'\) ein Quadrat mit der Seitenlänge \(3\sqrt{2}\) ist.
(4 BE)
Lösung zu Teilaufgabe c
Betrags eines Vektors, Orthogonalität zweier Vektoren
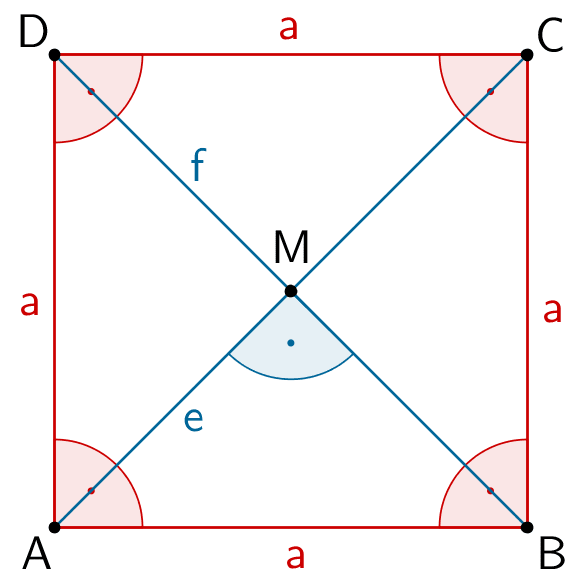
Merkmale eines Quadrats:
- Alle Seiten sind gleich lang. Dieses Merkmal gilt auch für eine Raute.
- Alle Innenwinkel betragen 90°. Dieses Merkmal gilt auch für ein Rechteck.
- Die Diagonalen \(e\) und \(f\) sind gleich lang und schneiden sich rechtwinklig im Mittelpunkt \(M\) der Diagonalen.
Das Viereck \(ABA'B'\) ist ein Quadrat mit der Seitenlänge \(3\sqrt{2}\), wenn beispielsweise
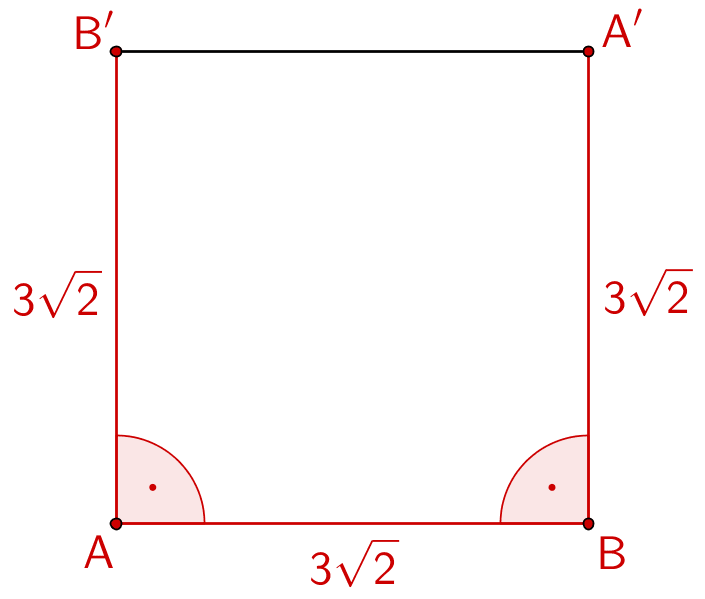
- drei Seiten die Länge \(3\sqrt{2}\) haben und die jeweils anliegenden Seiten einen rechten Winkel einschließen.
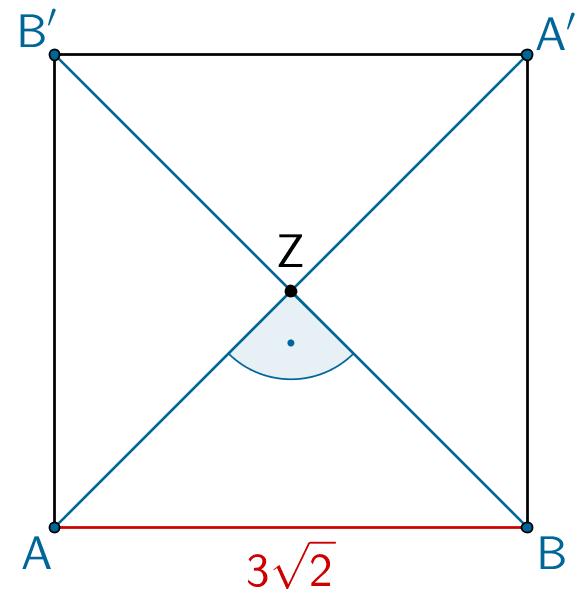
- die Diagonalen \([AA']\) und \(BB'\) gleich lang sind und diese sich rechtwinklig im Mittelpunkt der Diagonalen schneiden, sowie eine Seite die Länge \(3\sqrt{2}\) hat.
Wählt man eine dieser Vorgehensweisen, müssen die Koordinaten der Bildpunkte \(A'\) und \(B'\) berechnet werden. Dies lässt sich umgehen, wenn man die besondere Lage des Punktes \(Z\) berücksichtigt.
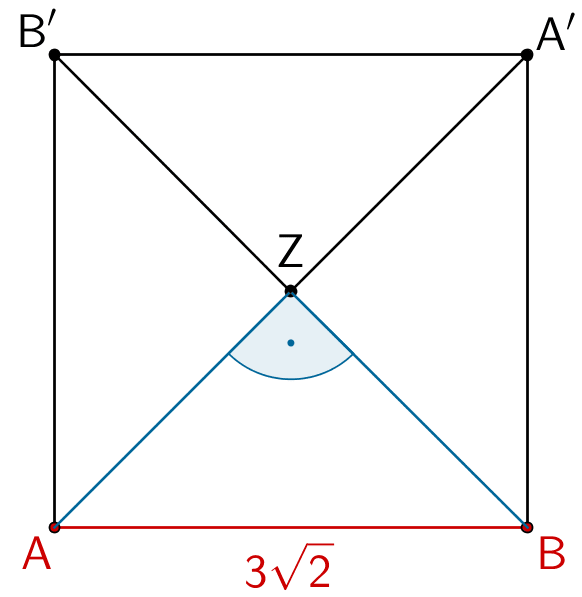
Da die Punkte \(A'\) und \(B'\) jeweils durch Spiegelung der Punkte \(A\) und \(B\) am Punkt \(Z\) hervorgehen, ist \(Z\) der Mittelpunkt der Diagonalen \([AA']\) und \([BB']\). Weist man nach, dass die Strecken \([ZA]\) und \([ZB]\) gleich lang und senkrecht zueinander sind, folgt daraus, dass sich die gleichlangen Diagonalen \([AA']\) und \([BB']\) rechtwinklig in \(Z\) schneiden. Anschließend bestätigt man, dass \(\overline{AB} = 3\sqrt{2}\) gilt und schlussfolgert daraus, dass das Viereck \(ABA'B'\) ein Quadrat mit der Seitenlänge \(3\sqrt{2}\) ist.
1. Lösungsansatz: Berücksichtigung der Lage des Punktes \(Z\) (ohne Berechnung von \(A'\) und \(B'\))
Verbindungsvektoren berechnen:
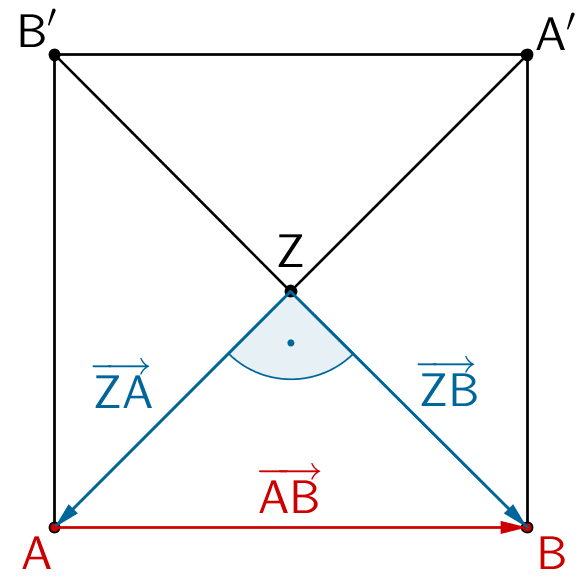
Für die Überprüfung der Längen der Strecken \([ZA]\), \([ZB]\) und \([AB]\) werden beispielsweise die Verbindungsvektoren \(\overrightarrow{ZA}\), \(\overrightarrow{ZB}\) und \(\overrightarrow{AB}\) berechnet. Außerdem wird die Orthogonalität der Vektoren \(\overrightarrow{ZA}\) und \(\overrightarrow{ZB}\) überprüft.
\(A(6|3|3)\), \(B(3|6|3)\), \(Z(3|3|3)\)
\[\overrightarrow{ZA} = \overrightarrow{A} - \overrightarrow{Z} = \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}\]
\[\overrightarrow{ZB} = \overrightarrow{B} - \overrightarrow{Z} = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\]
Längen der Strecken \([ZA]\), \([ZB]\) und \([AB]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(\overrightarrow{ZA} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}\), \(\overrightarrow{ZB} = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix}\), \(\overrightarrow{AB} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\)
\[\overline{ZA} = \vert \overrightarrow{ZA} \vert = \left| \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \right| = \sqrt{3^{2} + 0^{2} + 0^{2}} = 3\]
\[\overline{ZB} = \vert \overrightarrow{ZB} \vert = \left| \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix} \right| = \sqrt{0^{2} + 3^{2} + 0^{2}} = 3\]
\[\overline{AB} = \vert \overrightarrow{AB} \vert = \left| \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix} \right| = \sqrt{(-3)^{2} + 3^{2} + 0^{2}} = \sqrt{18} = 3\sqrt{2}\]
\[\Longrightarrow \quad \overline{ZA} = \overline{ZB} = 3 \quad \Longrightarrow \quad \overline{AA'} = \overline{BB'} = 6\]
Die Diagonalen \([AA']\) und \([BB']\) des Vierecks \(ABA'B'\) sind gleich lang.
Ortogonalität der Vektoren \(\overrightarrow{ZA}\) und \(\overrightarrow{ZB}\) prüfen:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\(\overrightarrow{ZA} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}\), \(\overrightarrow{ZB} = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix}\)
\[\overrightarrow{ZA} \circ \overrightarrow{ZB} = 0 \quad \Longleftrightarrow \quad \overrightarrow{ZA} \perp \overrightarrow{ZB}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\overrightarrow{ZA} \circ \overrightarrow{ZB} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix} = 3 \cdot 0 + 0 \cdot 3 + 0 \cdot 0 = 0\]
\[\Longrightarrow \quad \overrightarrow{ZA} \perp \overrightarrow{ZB} \quad \Longrightarrow \quad [AA'] \perp [BB']\]
Die Diagonalen \([AA']\) und \([BB']\) des Vierecks \(ABA'B'\) sind zueinander senkrecht.
Schlussfolgerung:

\[\left. \begin{align*} &\overline{AA'} = \overline{BB'} \\[0.8em] &[AA'] \perp [BB'] \\[0.8em] &\overline{AB} = 3\sqrt{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Quadrat}\; ABA'B' \; \text{mit Seitenlänge} \; 3\sqrt{2}\]
Das Viereck \(ABA'B'\) ist ein Quadrat mit der Seitenlänge \(3\sqrt{2}\).
2. Lösungsansatz: Drei gleich lange Seiten und Orthogonalität der anliegenden Seiten (mit Berechnung von \(A'\) und \(B'\))
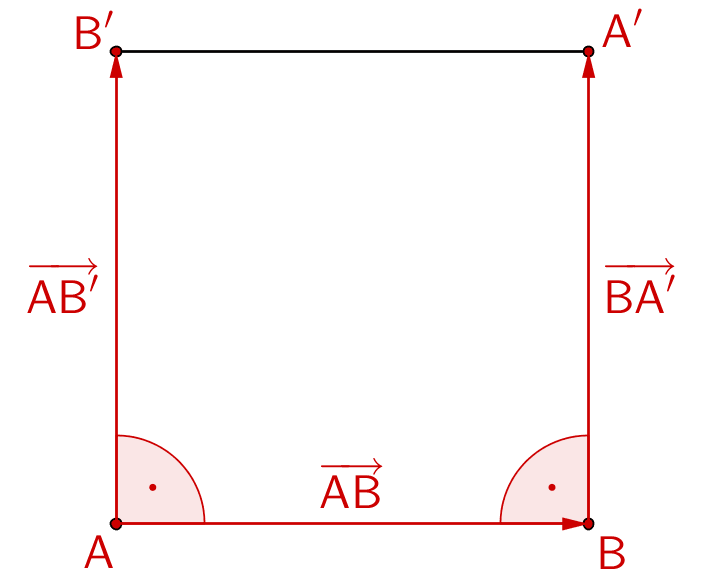
Um die Längen dreier Seiten sowie die Orthogonalität je zweier anliegender Seiten des Vierecks \(ABA'B'\) überprüfen zu können, werden beispielsweise die Verbindungsvektoren \(\overrightarrow{AB}\), \(\overrightarrow{AB'}\) und \(\overrightarrow{BA'}\) bestimmt.
Hierfür müssen zunächst die Koordinaten der Bildpunkte \(A'\) und \(B'\) berechnet werden.
Berechnung der Koordinaten der Bildpunkte \(A'\) und \(B'\):
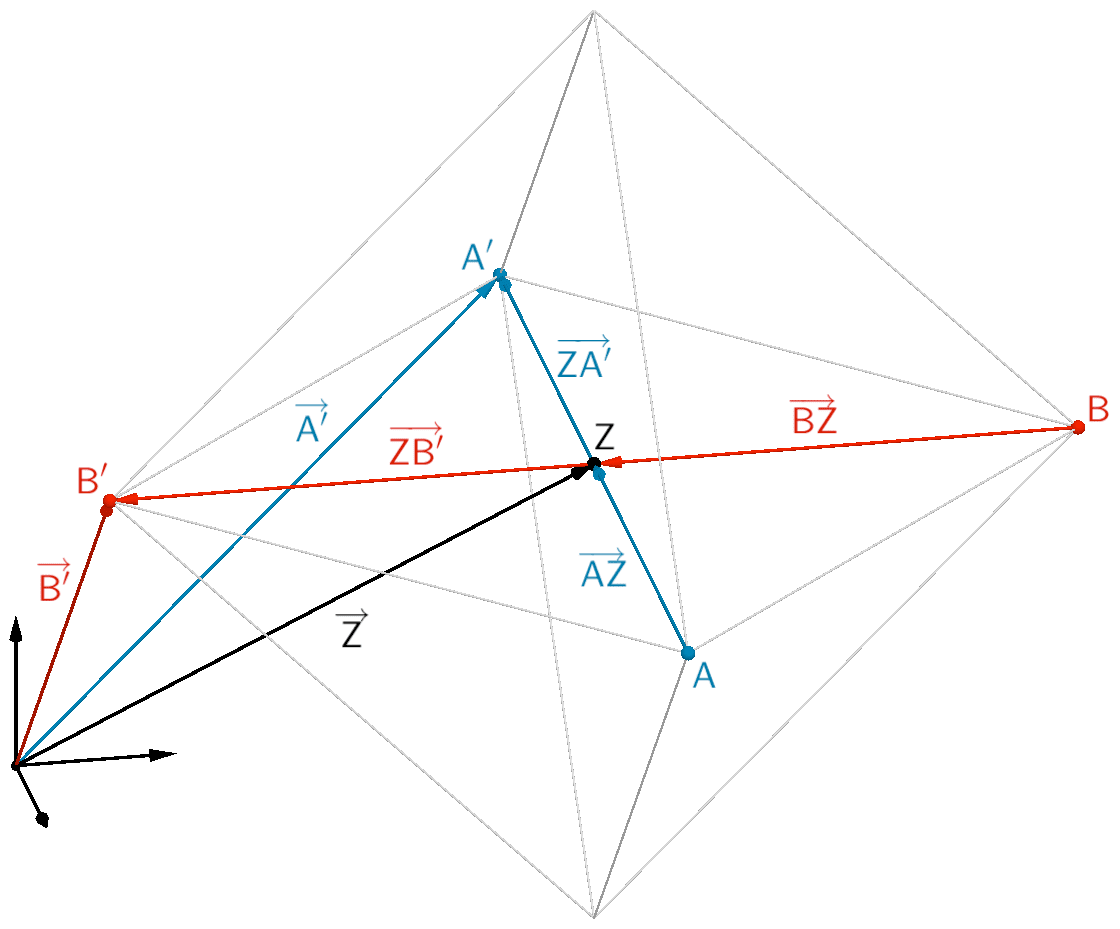
Der Bildpunkt \(A'\) bzw. \(B'\) geht durch Spiegelung des Punktes \(A\) bzw. \(B\) am Punkt \(Z\) hervor. Die Koordinaten der Ortsvektoren \(\overrightarrow{A'}\) bzw. \(\overrightarrow{B'}\) lassen sich durch Vektoraddition berechnen.
\(A(6|3|3)\), \(B(3|6|3)\), \(Z(3|3|3)\)
\[\begin{align*} \overrightarrow{A'} &= \overrightarrow{Z} + \overrightarrow{ZA'} & &| \; \overrightarrow{ZA'} = \overrightarrow{AZ} \\[0.8em] &= \overrightarrow{Z} + \overrightarrow{AZ} \\[0.8em] &= \overrightarrow{Z} + \overrightarrow{Z} - \overrightarrow{A} \\[0.8em] &= 2 \cdot \overrightarrow{Z} - \overrightarrow{A} \\[0.8em] &= 2 \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 3 \\ 3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad A'(0|3|3)\]
\[\begin{align*} \overrightarrow{B'} &= \overrightarrow{Z} + \overrightarrow{ZB'} & &| \; \overrightarrow{ZB'} = \overrightarrow{BZ} \\[0.8em] &= \overrightarrow{Z} + \overrightarrow{BZ} \\[0.8em] &= \overrightarrow{Z} + \overrightarrow{Z} - \overrightarrow{B} \\[0.8em] &= 2 \cdot \overrightarrow{Z} - \overrightarrow{B} \\[0.8em] &= 2 \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3 \\ 0 \\ 3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad B'(3|0|3)\]
oder
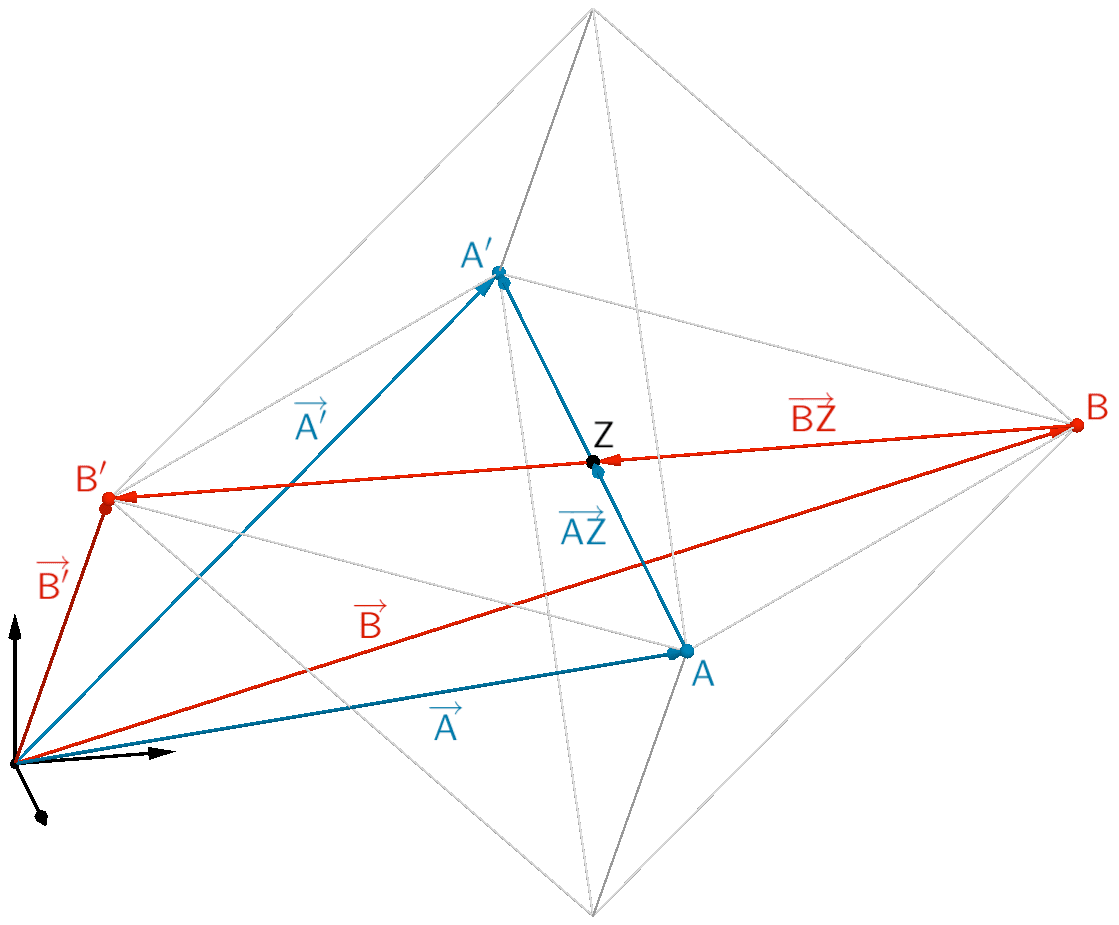
\[\begin{align*} \overrightarrow{A'} &= \overrightarrow{A} + 2 \cdot \overrightarrow{AZ} \\[0.8em] &= \overrightarrow{A} + 2 \cdot \left( \overrightarrow{Z} - \overrightarrow{A} \right) \\[0.8em] &= \overrightarrow{A} + 2 \cdot \overrightarrow{Z} - 2 \cdot \overrightarrow{A} \\[0.8em] &= 2 \cdot \overrightarrow{Z} - \overrightarrow{A} \\[0.8em] &= 2 \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 3 \\ 3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad A'(0|3|3)\]
\[\begin{align*} \overrightarrow{B'} &= \overrightarrow{B} + 2 \cdot \overrightarrow{BZ} \\[0.8em] &= \overrightarrow{B} + 2 \cdot \left( \overrightarrow{Z} - \overrightarrow{B} \right) \\[0.8em] &= \overrightarrow{B} + 2 \cdot \overrightarrow{Z} - 2 \cdot \overrightarrow{B} \\[0.8em] &= 2 \cdot \overrightarrow{Z} - \overrightarrow{B} \\[0.8em] &= 2 \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3 \\ 0 \\ 3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad B'(3|0|3)\]
Verbindungsvektoren \(\overrightarrow{AB}\), \(\overrightarrow{AB'}\) und \(\overrightarrow{BA'}\) berechnen:
\(A(6|3|3)\), \(B(3|6|3)\), \(A'(0|3|3)\), \(B'(3|0|3)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\]
\[\overrightarrow{AB'} = \overrightarrow{B'} - \overrightarrow{A} = \begin{pmatrix} 3 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} = \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix}\]
\[\overrightarrow{BA'} = \overrightarrow{A'} - \overrightarrow{B} = \begin{pmatrix} 0 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} = \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{AB'} = \overrightarrow{BA'}\]
Längen der Strecken \([AB]\), \([AB']\) und \([BA']\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(\overrightarrow{AB} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\), \(\overrightarrow{AB'} = \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix}\), \(\overrightarrow{BA'} = \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix}\)
\[\overline{AB} = \vert \overrightarrow{AB} \vert = \left| \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix} \right| = \sqrt{(-3)^{2} + 3^{2} + 0^{2}} = \sqrt{18} = 3\sqrt{2}\]
\[\begin{align*}\overline{AB'} = \overline{BA'} &= \vert \overrightarrow{BA'} \vert \\[0.8em] &= \left| \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-3)^{2} + (-3)^{2} + 0^{2}} \\[0.8em] &= \sqrt{18} \\[0.8em] &= 3\sqrt{2} \end{align*}\]
\[\Longrightarrow \overline{AB} = \overline{AB'} = \overline{BA'} = 3\sqrt{2}\]
Die Seiten \([AB]\), \([AB']\) und \([BA']\) des Vierecks \(ABA'B'\) sind gleich lang.
Ortogonalität der Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AB'}\) sowie \(\overrightarrow{AB}\) und \(\overrightarrow{BA'}\) prüfen:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\(\overrightarrow{AB} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\), \(\overrightarrow{AB'} = \overrightarrow{BA'} = \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix}\)

Da \(\overrightarrow{AB'} = \overrightarrow{BA'}\) gilt, reicht es aus, die Orthogonalität der Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AB'}\) zu prüfen.
\[\overrightarrow{AB} \circ \overrightarrow{AB'} = 0 \quad \Longleftrightarrow \quad \overrightarrow{AB} \perp \overrightarrow{AB'}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\overrightarrow{AB} \circ \overrightarrow{AB'} &= \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix} \circ \begin{pmatrix} -3 \\ -3 \\ 0 \end{pmatrix} \\[0.8em] &= (-3) \cdot (-3) + 3 \cdot (-3) + 0 \cdot 0 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{AB} \perp \overrightarrow{AB'} \quad \Longrightarrow \quad [AB] \perp [AB'], \, [AB] \perp [BA']\]
Die Seiten \([AB]\) und \([AB']\) sowie \([AB]\) und \([BA']\) des Vierecks \(ABA'B'\) sind zueinander senkrecht.
Schlussfolgerung:

\[\left. \begin{align*} &\overline{AB} = \overline{AB'} = \overline{BA'} = 3\sqrt{2} \\[0.8em] &[AB] \perp [AB'], \, [AB] \perp [BA'] \end{align*} \right\} \enspace \Rightarrow \enspace \text{Quadrat}\; ABA'B' \; \text{mit Seitenlänge} \; 3\sqrt{2}\]
Das Viereck \(ABA'B'\) ist ein Quadrat mit der Seitenlänge \(3\sqrt{2}\).


