Bestimmen Sie eine Gleichung der Tangente \(t\) an \(G_f\) im Punkt \((10|f(10))\) und zeichnen Sie \(t\) für \(x \geq 10\) in Abbildung 1 ein.
(zur Kontrolle: Gleichung von \(t \colon y = -0{,}12x + 3\))
(4 BE)
Lösung zu Teilaufgabe 1d
Gleichung der Tangente \(t\) an \(G_f\) im Punkt \((10|f(10))\)
\[f(x) = \frac{1}{100}\left(2x^3-43x^2 + 248x\right); \; D_f = \mathbb R\]
Ansatz: \(t \colon y = \textcolor{#cc071e}{m}x + \textcolor{#e9b509}{b}\)
1. Tangentensteigung berechnen:
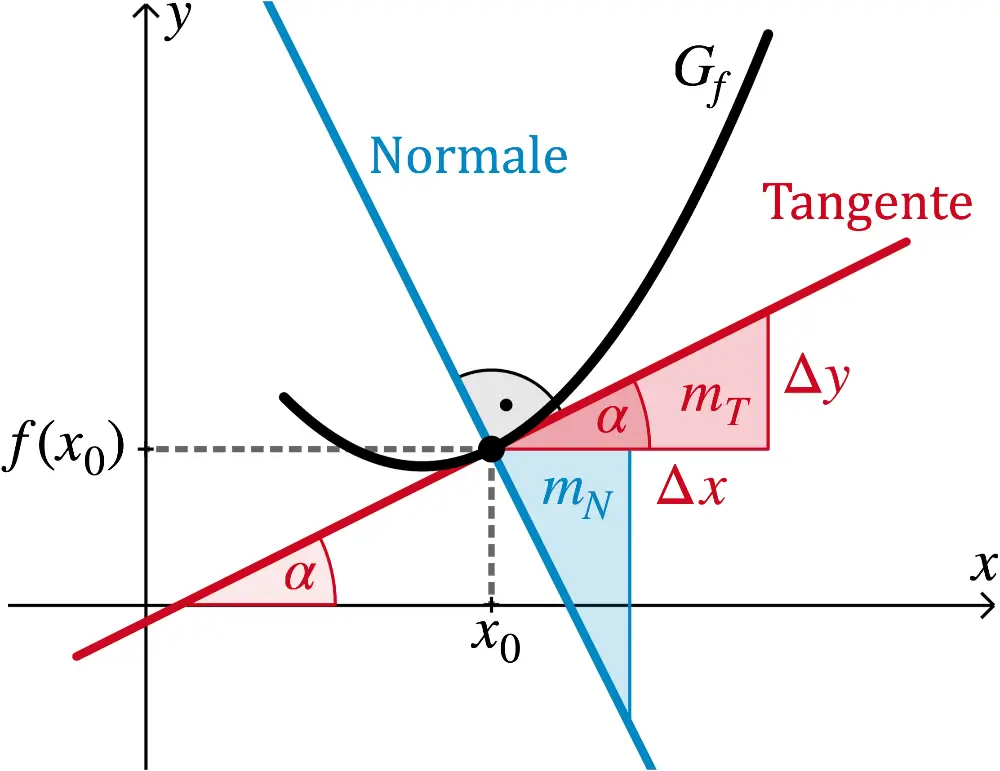
Tangentensteigung und Normalensteigung
\[\textcolor{#cc071e}{m_{T}} = f'(x_0) \qquad \textcolor{#0087c1}{m_{N}} = -\dfrac{1}{f'(x_0)}\]
Steigungswinkel \(\boldsymbol{\alpha}\) einer Tangente
\[{\textcolor{#cc071e}{\tan{\alpha}}} = f'(x_0)\]
\[\textcolor{#cc071e}{m} = f'(10)\]
\(f'(x) = \dfrac{1}{100} \cdot \left(6x^2 -86x +248\right)\) (vgl. Teilaufgabe b)
\[\textcolor{#cc071e}{m} = \frac{1}{100} \cdot \left( 6 \cdot 10^2 - 86 \cdot 10 + 248 \right) = \textcolor{#cc071e}{-0{,}12}\]
2. \(\textcolor{#e9b509}{y}\)-Achsenabschnitt \(\textcolor{#e9b509}{b}\) bestimmen:
Punkt \((\textcolor{#89ba17}{10}|\textcolor{#89ba17}{f(10)})\)
\[\textcolor{#89ba17}{f(10)} = \frac{1}{100}\left( 2 \cdot \textcolor{#89ba17}{10}^3 - 43 \cdot \textcolor{#89ba17}{10}^2 + 284 \cdot \textcolor{#89ba17}{10}\right) = \textcolor{#89ba17}{1{,}8}\; \Rightarrow \; (\textcolor{#89ba17}{10}|\textcolor{#89ba17}{1{,}8})\]
Wert von \(\textcolor{#cc071e}{m}\) und Koordiaten von Punkt \((\textcolor{#89ba17}{10}|\textcolor{#89ba17}{1{,}8})\) in den Ansatz \(y = \textcolor{#cc071e}{m}x + \textcolor{#e9b509}{b}\) einsetzen und nach dem \(\textcolor{#e9b509}{y}\)-Achsenabschnitt \(\textcolor{#e9b509}{b}\) auflösen.
\[\textcolor{#89ba17}{1{,}8} = \textcolor{#cc071e}{-0{,}12} \cdot \textcolor{#89ba17}{10} + \textcolor{#e9b509}{b} \; \Leftrightarrow \; \textcolor{#e9b509}{b} = 1{,}8 + 1{,}2 = \textcolor{#e9b509}{3}\]
3. Tangentengleichung angeben:
\[t \colon y = -0{,}12x + 3\]
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.2.2 Tangentensteigung und Tagentengleichung - Tangentenaufgabe Variante I)
Einzeichnen der Tangente \(t\) für \(x \geq 10\) in Abbildung 1
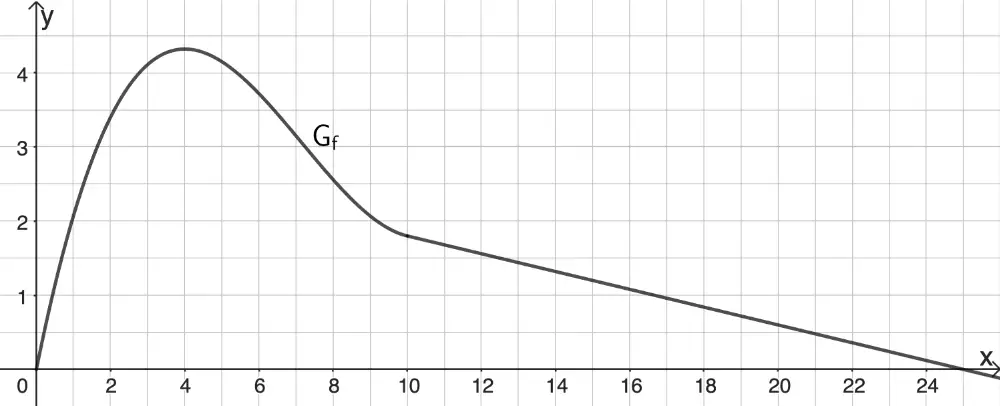
Graph der Funktion \(f \colon x \mapsto \frac{1}{100}\left( 2x^3-43x^2+248x \right)\) für \(0 \leq x \leq 10\) und Tangente \(t\) im Punkt \((10|f(10))\) für \(x \geq 10\)


