Berechnen Sie die Stelle \(x_{m}\) im Intervall \([2;8]\), an der die lokale Änderungsrate von \(f\) gleich der mittleren Änderungsrate in diesem Intervall ist.
(5 BE)
Lösung zu Teilaufgabe 2b
\[f(x) = 2 - \ln{(x - 1)}; \; D_{f} = \; ]1;+\infty[\]
Die mittlere Änderungsrate \(m\) im Intervall \([2;8]\) ist gegeben durch:
Differenzenquotient oder mittlere Änderungsrate
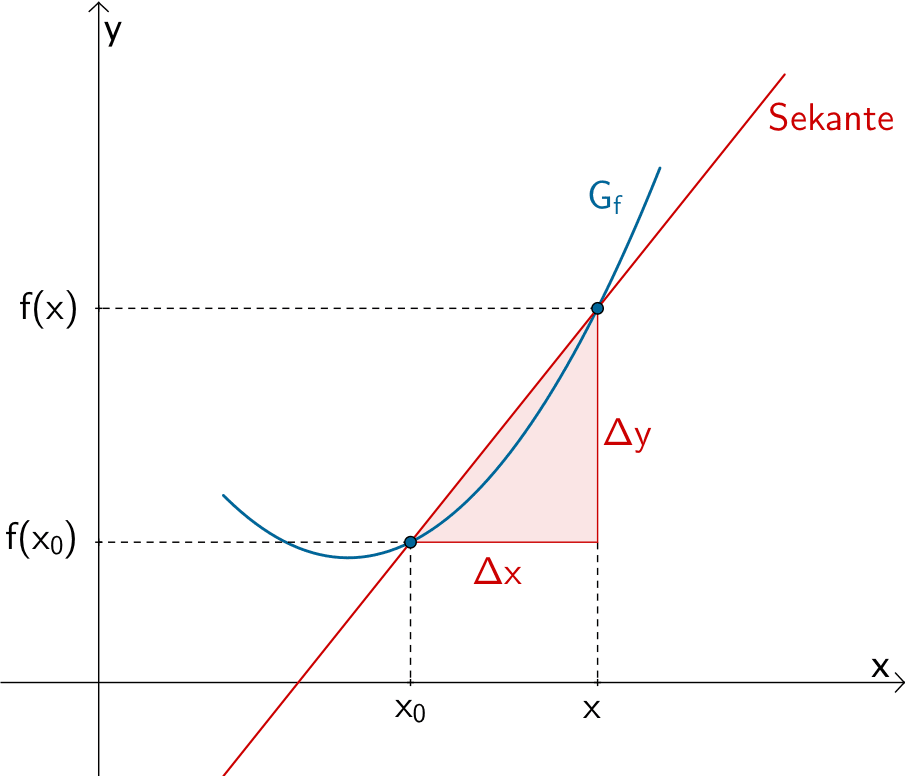
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[m = \frac{f(8) - f(2)}{8 - 2}\]
Die lokale Änderungsrate von \(f\) an der Stelle \(x_{m}\) ist gegeben durch:
Differentialquotient oder lokale bzw. momentane Änderungsrate
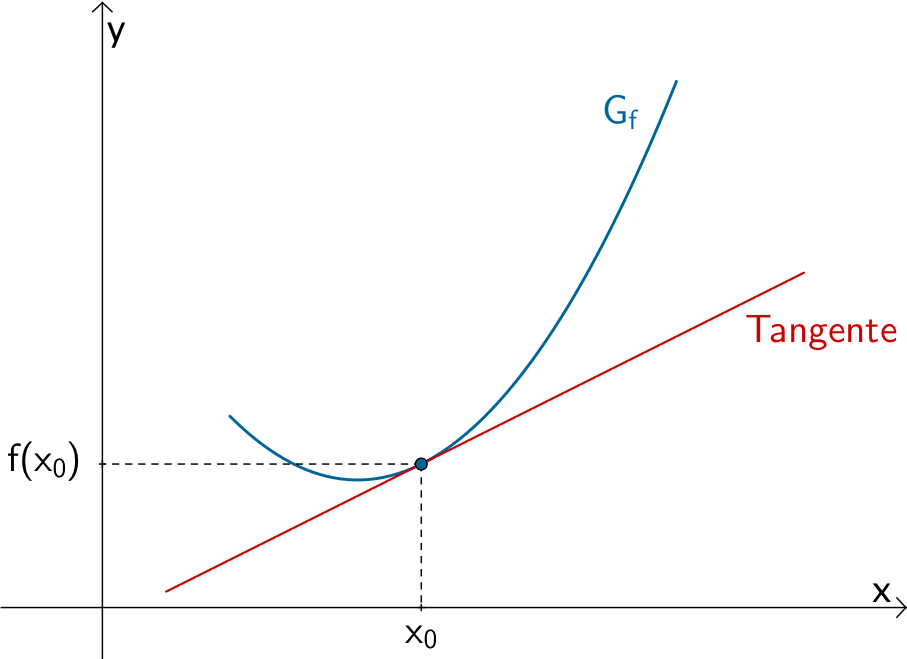
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\[f'(x_{m})\]
Für die Gleichheit der mittleren und der lokalen Änderungsrate im Intervall \([2;8]\) muss also gelten:
\[m = f'(x_{m}); \; x_{m} \in [2;8]\]
Erste Ableitung \(f'\) bilden:
Hierfür wird die Ableitung einer Konstante, die Ableitung der Natürlichen Logarithmusfunktion sowie die Kettenregel benötigt.
\[f(x) = 2 - \ln{(x - 1)}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[f'(x) = 0 - \frac{1}{x - 1} \cdot 1 = \frac{1}{1 - x}\]
Stelle \(x_{m}\) berechnen:
\[\begin{align*} m &= f'(x_{m}) &&| \; x_{m} \in [2;8] \\[0.8em] \frac{f(8) - f(2)}{8 - 2} &= \frac{1}{1 - x_{m}} \\[0.8em] \frac{2 - \ln{(8 - 1)} - \left[ 2 - \ln{(2 - 1)} \right]}{6} &= \frac{1}{1 - x_{m}} \\[0.8em] \frac{2 - \ln{7} - 2 + \ln{1}}{6} &= \frac{1}{1 - x_{m}} &&| \; \ln{1} = 0; \; \left(\text{allg.:}\; \log_{a}{1} = 0 \right) \\[0.8em] \frac{-\ln{7}}{6} &= \frac{1}{1 - x_{m}} &&| \; \text{„überkreuz" multiplizieren} \\[0.8em] (-\ln{7}) \cdot (1 - x_{m}) &= 6 &&| : (-\ln{7}) \\[0.8em] 1 - x_{m} &= -\frac{6}{\ln{7}} &&| + x_{m} + \frac{6}{\ln{7}} \\[0.8em] 1 + \frac{6}{\ln{7}} &= x_{m} \end{align*}\]
An der Stelle \(x_{m} = 1 + \dfrac{6}{\ln{7}} \approx 4{,}1\) ist die lokale Änderungsrate von \(f\) gleich der mittleren Änderungsrate im Intervall \([2;8]\).


