Lagebeziehung Punkt - Kugel

Die gegenseitige Lage zwischen einem Punkt \(P\) und einer Kugel \(K\) mit dem Mittelpunkt \(M\) wird durch den Abstand \(d(P;M) = \vert \overrightarrow{MP} \vert\) bestimmt.

Es lassen sich drei Fälle unterscheiden:

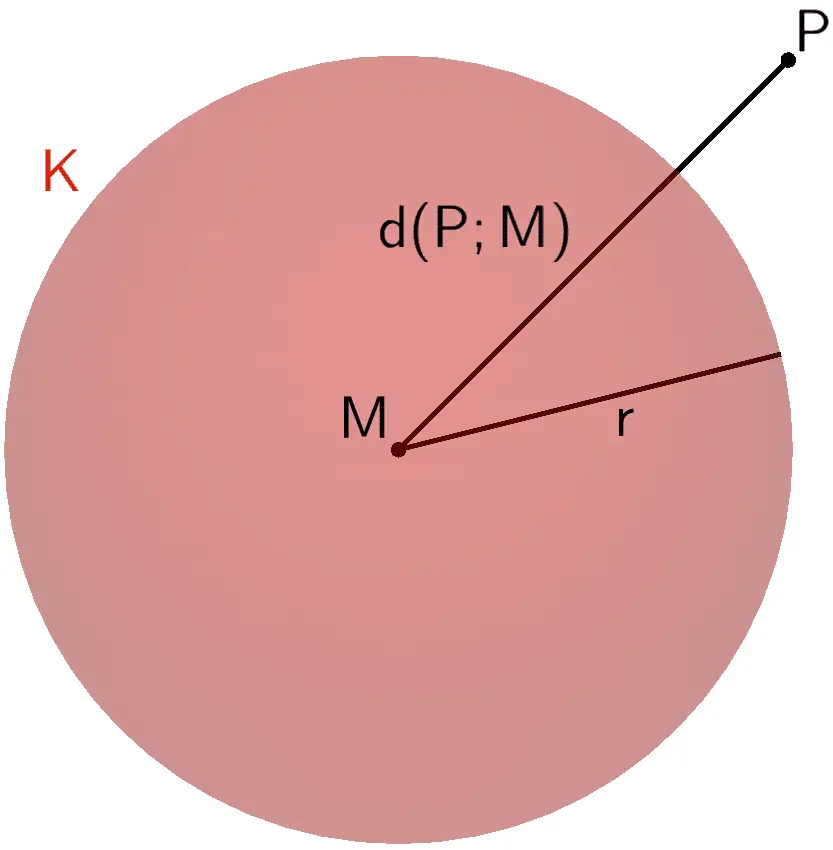
Der Punkt \(P\) liegt außerhalb der Kugel \(K\).

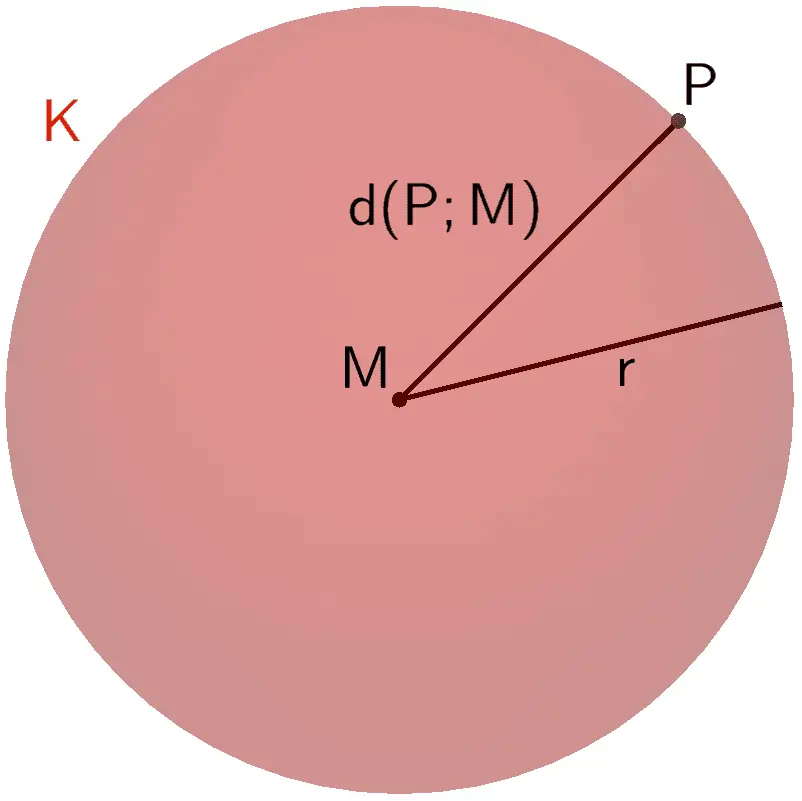
Der Punkt \(P\) liegt auf der Kugel \(K\).

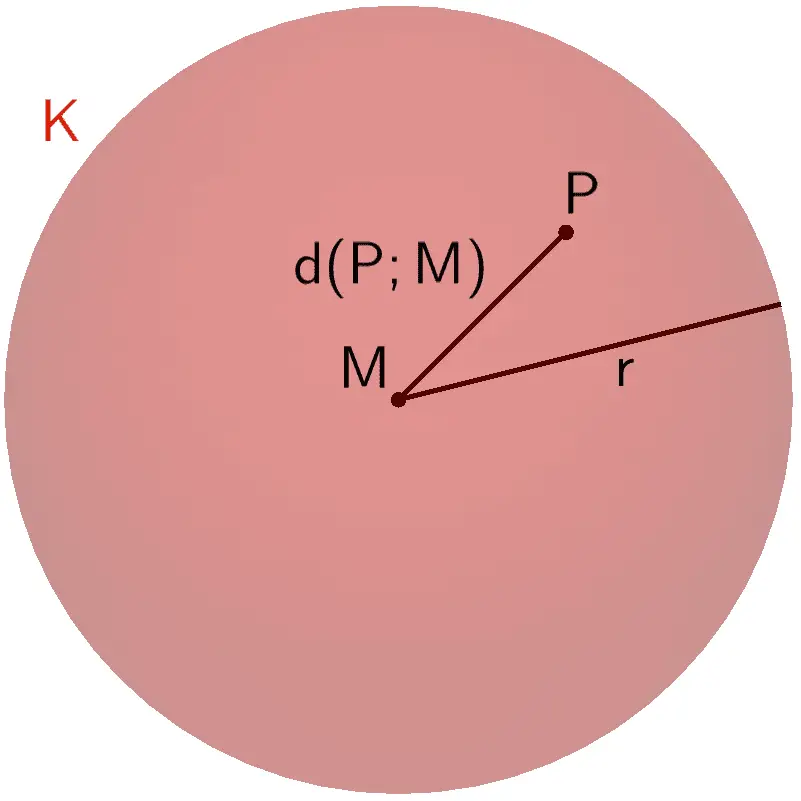
Der Punkt \(P\) liegt innerhalb der Kugel \(K\).

Beispielaufgabe

Gegeben sei der Punkt \(P(5|-1|8)\) sowie die Kugel \(K\colon (x_{1} - 7)^{2} + (x_{2} + 4)^{2} + (x_{3} - 1)^{2} = 7^{2}\).

Bestimmen Sie die Lagebeziehung des Punktes \(P\) und er Kugel \(K\) durch Rechnung.

\[K\colon (x_{1} - 7)^{2} + (x_{2} + 4)^{2} + (x_{3} - 1)^{2} = 7^{2}\]

\[\Longrightarrow \quad M(7|-4|1), \; r = 7\]

Abstand \(d(P;M)\) berechnen:

\(M(7|-4|1)\), \(P(5|-1|8)\)

\[\begin{align*} d(P;M) &= \vert \overrightarrow{MP} \vert \\[0.8em] &= \vert \overrightarrow{P} - \overrightarrow{M} \vert \\[0.8em] &= \left| \begin{pmatrix} 5 \\ -1 \\ 9 \end{pmatrix} - \begin{pmatrix} 7 \\ -4 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 3 \\ 7 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-2)^{2} + 3^{2} + 7^{2}} \\[0.8em] &= \sqrt{62} \\[0.8em] &\approx 7{,}87 \end{align*}\]

Schlussfolgerung:

\(r = 7\), \(d(P;M) \approx 7{,}87\)

\[\Longrightarrow \quad d(P;M) > r\]

\(\Longrightarrow \quad\)Der Punkt \(P\) liegt außerhalb der Kugel \(K\).