Die Abbildung zeigt den Graphen \(G_g\) der in \(\mathbb R\) definierten Funktion \(g\) mit \(g(x) = 2 \cdot \sin{\left( \dfrac{1}{2}x \right)}\).
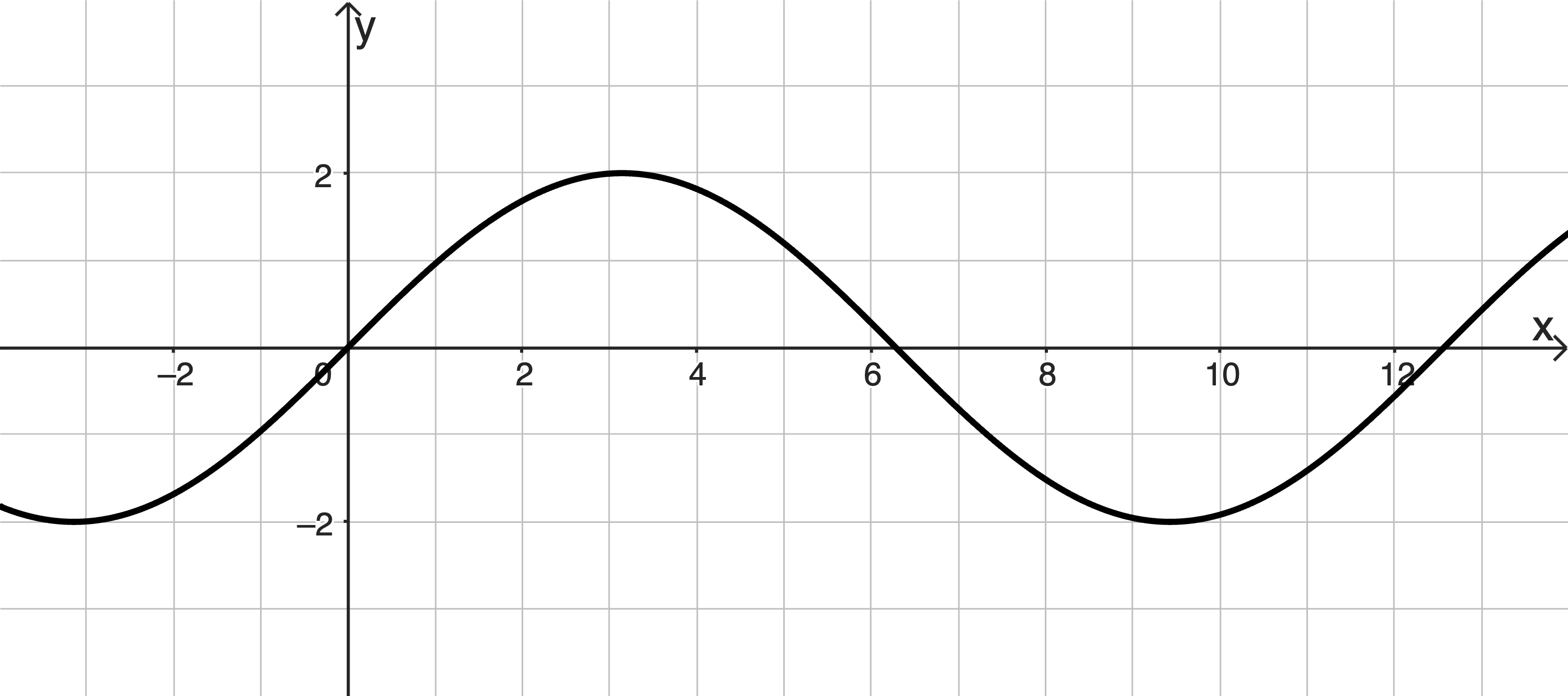
Beurteilen Sie mithilfe der Abbildung, ob der Wert des Integrals \(\displaystyle \int_{-2}^8 g(x)dx\) negativ ist.
(2 BE)
Lösung zu Teilaufgabe 2a
![Veranschaulichung der Flächenbilanz der Flächen, die der Graph von g im Intervall [-2;8] mit der x-Achse einschließt.](/images/stories/B2024_PT_A_A1/B2024_PT_A_A1_2_web.png)
Der Wert des bestimmten Integrals \(\displaystyle \int_{-2}^8 g(x)dx\) entspricht der Flächenbilanz der Flächen, die der Graph \(G_g\) im Intervall \([-2;8]\) mit der \(x\)-Achse einschließt. Dabei zählen Flächen oberhalb der \(x\)-Achse positiv und Flächen unterhalb der \(x\)-Achse negativ.
Da der Inhalt der oberhalb der \(x\)-Achse liegenden Fläche größer ist als der Inhalt der unterhalb der \(x\)-Achse liegenden Fläche, ist der Wert des Integrals positiv.


