Die binomialverteilte Zufallsgröße \(X\) mit den Parametern \(n = 8\) und \(p_X\) besitzt die Standardabweichung \(\frac{4}{3}\). In Abbildung 2 ist die Wahrscheinlichkeitsverteilung von \(X\) dargestellt.
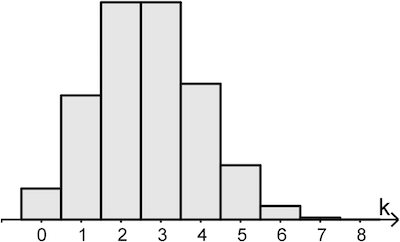 Abb. 2
Abb. 2
Ermitteln Sie den Wert des Parameters \(p_X\).
(4 BE)
Lösung zu Teilaufgabe 3a
\(\textcolor{#0087c1}{n = 8}\); \(\sigma = \dfrac{4}{3}\)
Die Zufallsgröße \(X\) ist nach \(B(\textcolor{#0087c1}{8};\textcolor{#cc071e}{p_X})\) binomialverteilt.
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist. \(Var(X)\) bezeichnet die Varianz der Zufallsgröße \(X\).
\[\begin{align*}\sigma &= \frac{4}{3}\\[0.8em] \sqrt{\textcolor{#0087c1}{8} \cdot \textcolor{#cc071e}{p_X} \cdot (1 - \textcolor{#cc071e}{p_X})} &= \frac{4}{3} &&| \; (\dots)^2\;\text{(Quadrieren)} \\[0.8em] 8 \cdot p_X \cdot (1 - p_X) &= \frac{16}{9} \\[0.8em] 8p_X - 8p_X^2 &= \frac{16}{9} &&| -\frac{16}{9}\;\text{(quadratische Gleichung formulieren)} \\[0.8em] -8p_X^2 + 8p_X -\frac{16}{9} &= 0 &&| : (-8) \, \text{(optional)} \\[0.8em] p_X^2 -p_X +\frac{2}{9} &= 0 &&| \; \text{Mitternachtsformel anwenden}\end{align*}\]
\[\begin{align*}p_{X_{1,2}} &= \frac{1 \pm \sqrt{(-1)^2 - 4 \cdot 1 \cdot \frac{2}{9}}}{2 \cdot 1} = \frac{1 \pm \sqrt{\frac{1}{9}}}{2} \\[0.8em] &= \frac{1 \pm \frac{1}{3}}{2} = \frac{1}{2} \pm \frac{1}{6}\end{align*}\]
\[p_{X_1} = \frac{1}{2} - \frac{1}{6} = \frac{3}{6} - \frac{1}{6} = \frac{2}{6} = \frac{1}{3}\]
\[p_{X_2} = \frac{1}{2} + \frac{1}{6} = \frac{3}{6} + \frac{1}{6} = \frac{4}{6} = \frac{2}{3}\]
Nun ist noch zu überprüfen, welche der beiden rechnerischen Lösungen für die in Abbildung 2 dargestellte Wahrscheinlichkeitsverteilung von \(X\) in Frage kommt.
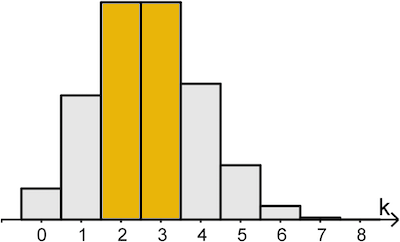 Abb. 2
Abb. 2
Abbildung 2 zeigt, dass die Wahrscheinlichkeiten \(\textcolor{#e9b509}{P(X = 2)}\) und \(\textcolor{#e9b509}{P(X = 3)}\) maximal sind. Deshalb muss der Erwartungswert \(\textcolor{#e9b509}{E(X)}\) zwischen \(\textcolor{#e9b509}{k = 2}\) und \(\textcolor{#e9b509}{k = 3}\) liegen.
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
Für \(p_X = \dfrac{1}{3}\) ergibt sich \(E(X) = 8 \cdot \dfrac{1}{3} = \dfrac{8}{3} = \textcolor{#e9b509}{2\dfrac{2}{3}}\).
Für \(p_X = \dfrac{2}{3}\) ergibt sich \(E(X) = 8 \cdot \dfrac{2}{3} = \dfrac{16}{3} = 5\dfrac{1}{3}\).
Folglich ist \(p_X = \dfrac{1}{3}\) die korrekte Lösung.


