Jede Ebene \(E_k\) der Schar schneidet die \(x_1x_2\)-Ebene in einer Gerade \(g_k\). Mit \(R_k\) wird jeweils derjenige Punkt auf \(g_k\) bezeichnet, der von \(O\) den kleinsten Abstand hat. In Abbildung 2 sind \(g_k\) und \(R_k\) beispielhaft für eine Ebene \(E_k\) der Schar dargestellt.

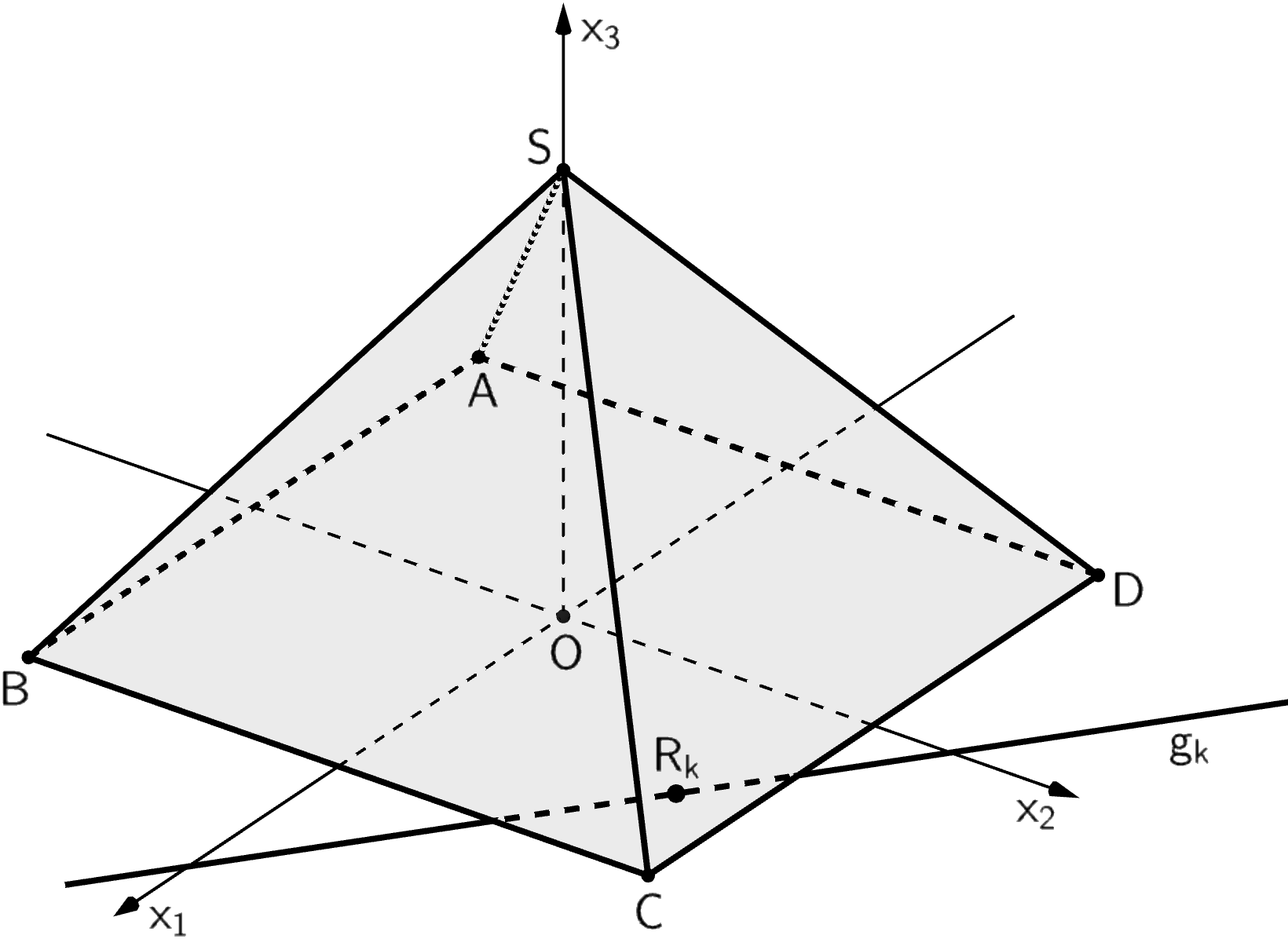Abbildung 2 Geometrie 2 Prüfungsteil B Mathematik Abitur Bayern 2024Abb. 2

Zeichnen Sie die Punkte \(R_{-1}\) und \(R_1\) in Abbildung 2 ein.

(2 BE)

Lösung zu Teilaufgabe g

 

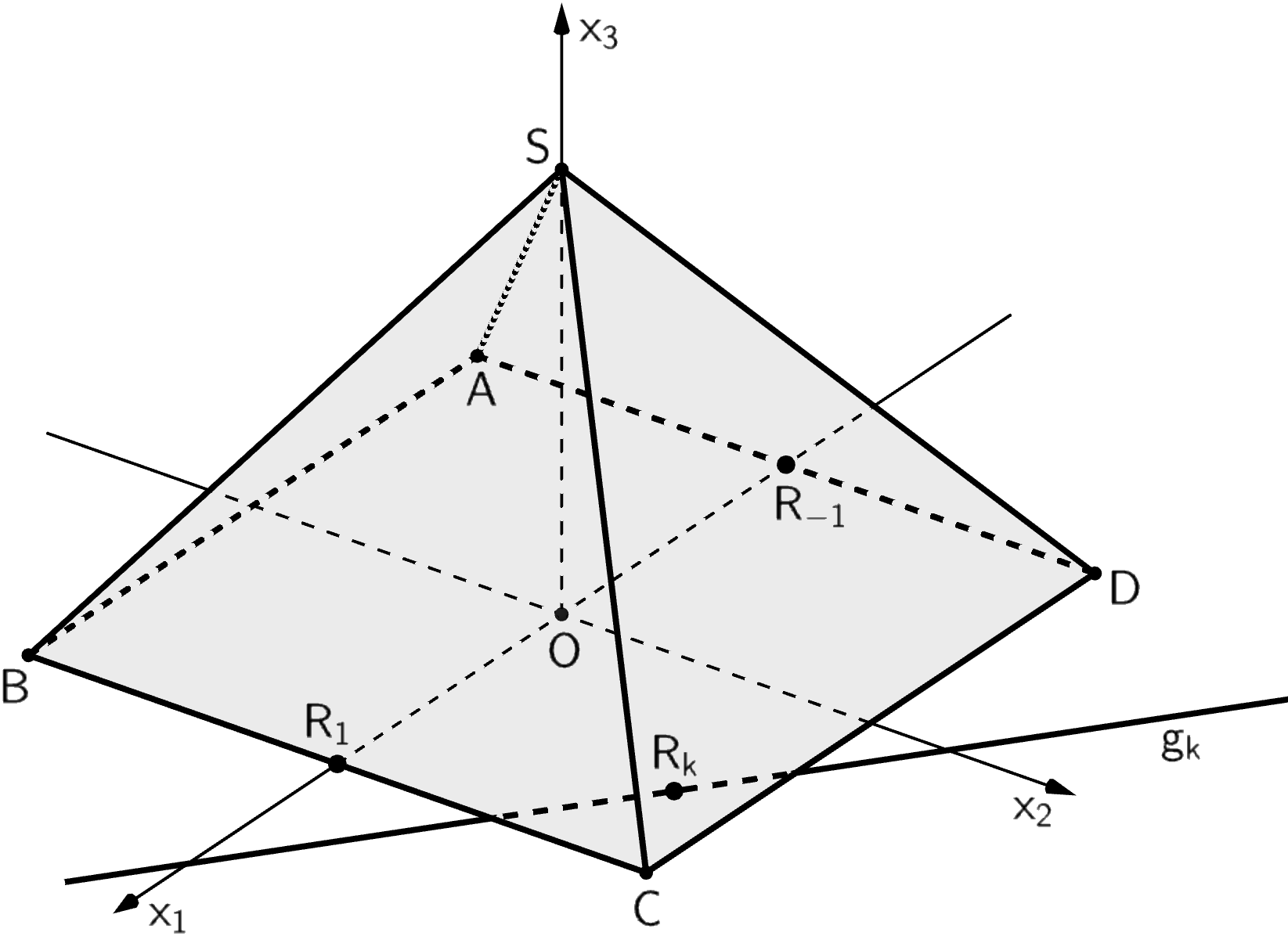Punkte R­­­₋₁ und R₁ in Abbildung 2 eingezeichnetAbb. 2

 

Ausführliche Erklärung (nicht verlangt)

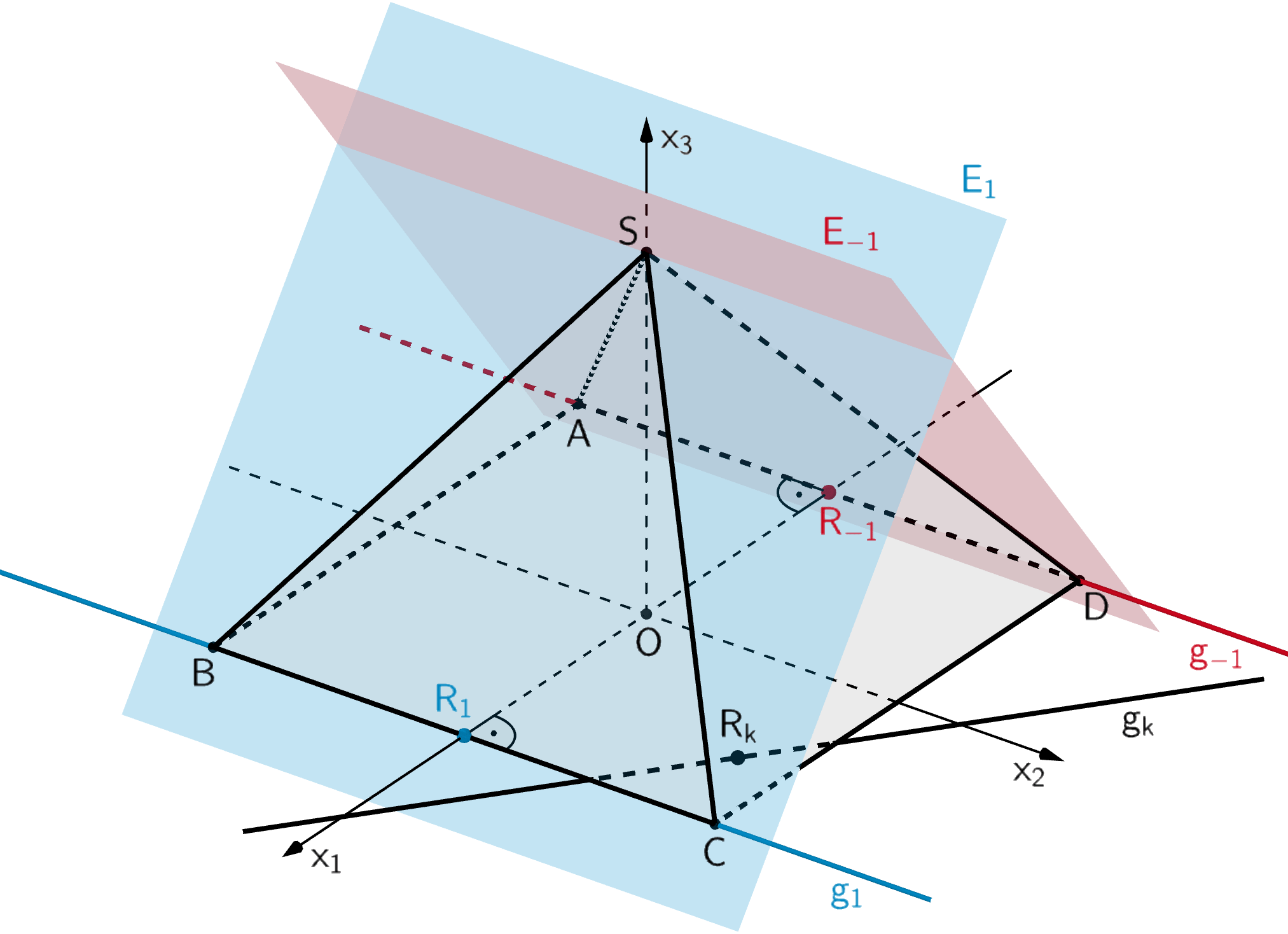
Ebene E₋₁, in der die Seitenfläche ADS liegt, mit Schnittgerade g₋₁ und Punkt R₋₁ sowie Ebene E₁, in der die Seitenfläche BCS liegt, mit Schnittgerade g₁ und Punkt R₁

Die Seitenfläche \(ADS\) liegt in der Ebene \(\textcolor{#cc071e}{R_{-1}}\) und die Seitenfläche \(BCS\) in der Ebene \(\textcolor{#0087c1}{E_1}\) (vgl. Angabe). Somit enthält die Schnittgerade \(\textcolor{#cc071e}{g_{-1}}\) die Grundlinie \([AD]\) und die Schnittgerade \(\textcolor{#0087c1}{g_1}\) die Grundlinie \([BC]\). Die \(x_1\)-Achse schneidet beide Grundlinien rechtwinklig. Die Schnittpunkte \(\textcolor{#cc071e}{R_{-1}}\) und \(\textcolor{#0087c1}{R_1}\) haben jeweils vom Koordinatenursprung \(O\) den kleinsten Abstand.