Das Skalarprodukt zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt eine reelle Zahl (Skalar: Maßzahl mit Maßeinheit).
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Sind die Koordinaten zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) gegeben, lässt sich das Skalarprodukt der beiden Vektoren als die Summe der Produkte der einzelnen Vektorkoordinaten berechnen.
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Anwendungen des Skalarprodukts
Mithilfe des Skalarprodukts lässt sich der Winkel zwischen zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) berechnen.
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos{\varphi} = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Eine weitere Anwendung ist das Prüfen, ob zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) senkrecht zueinander sind.
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} = 0 \quad (\overrightarrow{a} \neq \overrightarrow{0}, \overrightarrow{b} \neq \overrightarrow{0})\]
Auch kann der Betrag (die Länge) eines Vektors \(\overrightarrow{a}\) sowie dessen Einheitsvektor \(\overrightarrow{a}^{0}\) mithilfe des Skalarprodukts formuliert werden (vgl. 2.1.1 Rechnen mit Vektoren).
Betrag eines Vektors
\[\vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}\]
Einheitsvektor
\[\overrightarrow{a}^{0} = \frac{\overrightarrow{a}}{\vert \overrightarrow{a} \vert} = \frac{\overrightarrow{a}}{\sqrt{\overrightarrow{a} \circ \overrightarrow{a}}}\]
(vg. Merkhilfe)
Beispielaufgabe
Die Punkte \(A(8|2|0)\), \(B(4|7|6)\), \(C(0|4|6)\) und \(D(0|0|3)\) legen das Viereck \(ABCD\) fest.
Zeichnen Sie das Viereck \(ABCD\) in ein Koordinatensystem (vgl. Abbildung). Bestätigen Sie rechnerisch, dass das Viereck \(ABCD\) ein Drachenviereck ist.
Zeichnung des Vierecks \(ABCD\)
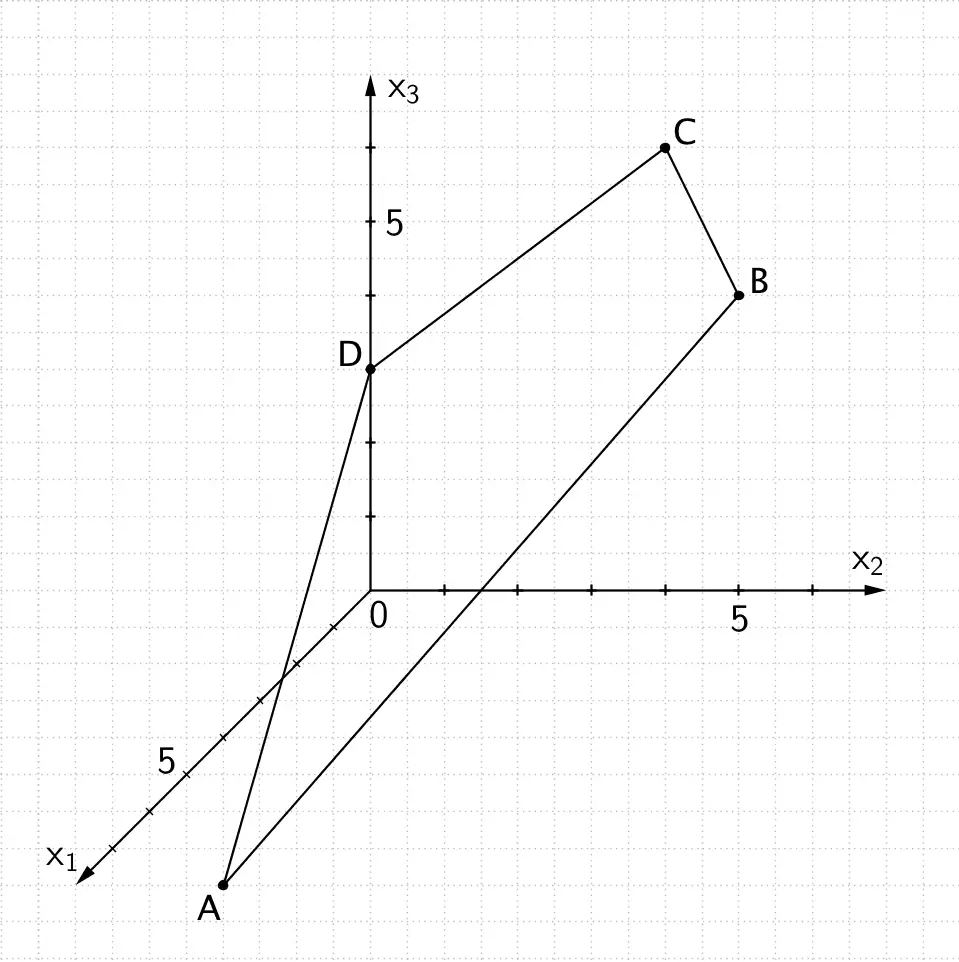
Viereck \(ABCD\): Die Zeichnung lässt erkennen, dass die Strecke \([AC]\) die Symmetrieachse des Drachenvierecks ist.
Nachweis, dass das Viereck \(ABCD\) ein Drachenviereck ist
![Drachenviereck ABCD, Diagonalen [AC] und [BD], Innenwinkel Drachenviereck ABCD, Diagonalen [AC] und [BD], Innenwinkel](/images/stories/abi_check/geometrie/Vektoren_SkalProd_Bsp.png)
Das Viereck \(ABCD\) ist ein Drachenviereck, wenn die Strecken \([AC]\) und \([BD]\) (Diagonalen des Drachenvierecks) senkrecht zueinander stehen und wenn die beiden bezgl. der Symmetrieachse \([AC]\) gegenüberliegenden Innenwinkel \(\beta\) und \(\delta\) gleich groß sind, sowie die beiden Innenwinkel \(\alpha\) und \(\gamma\) ungleich groß sind.
Nachweis der Ortogonalität der Strecken \([AC]\) und \([BD]\):
Mithilfe des Skalarprodukts weist man nach, dass die Vektoren \(\overrightarrow{AC}\) und \(\overrightarrow{BD}\) senkrecht zueinander sind.
\[\overrightarrow{AC} \perp \overrightarrow{BD} \quad \Longleftrightarrow \quad \overrightarrow{AC} \circ \overrightarrow{BD}\]
Verbindungsvektoren \(\overrightarrow{AC}\) und \(\overrightarrow{BD}\) berechnen:
\(A(8|2|0)\), \(B(4|7|6)\), \(C(0|4|6)\), \(D(0|0|3)\)
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 4 \\ 6 \end{pmatrix} - \begin{pmatrix} 8 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} -8 \\ 2 \\ 6 \end{pmatrix}\]
\[\overrightarrow{BD} = \overrightarrow{D} - \overrightarrow{B} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 4 \\ 7 \\ 6 \end{pmatrix} = \begin{pmatrix} -4 \\ -7 \\ -3 \end{pmatrix}\]
Skalarprodukt anwenden:
\[\begin{align*}\overrightarrow{AC} \circ \overrightarrow{BD} &= \begin{pmatrix} -8 \\ 2 \\ 6 \end{pmatrix} \circ \begin{pmatrix} -4 \\ -7 \\ -3 \end{pmatrix} \\[0.8em] &= (-8) \cdot (-4) + 2 \cdot (-7) + 6 \cdot (-3) \\[0.8em] &= 32 - 14 - 18 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{AC} \perp \overrightarrow{BD} \quad \Longrightarrow \quad [AC] \perp [BD]\]
Nachweis der Innenwinkel Beziehungen \(\beta = \delta\) und \(\alpha \neq \gamma\)
![Drachenviereck ABCD, Diagonalen [AC] und [BD], Innenwinkel Drachenviereck ABCD, Diagonalen [AC] und [BD], Innenwinkel](/images/stories/abi_check/geometrie/Vektoren_SkalProd_Bsp.png)
Man berechnet beispielsweise die Größe der Winkel \(\alpha\), \(\beta\) und \(\gamma\) mithilfe des Skalarprodukts und die Größe des Winkels \(\delta\) über die Innenwinkelsumme.
\[\cos{\alpha} = \dfrac{\overrightarrow{AD} \circ \overrightarrow{AB}}{\vert \overrightarrow{AD} \vert \cdot \vert \overrightarrow{AB} \vert}\]
\[\cos{\beta} = \dfrac{\overrightarrow{BA} \circ \overrightarrow{BC}}{\vert \overrightarrow{BA} \vert \cdot \vert \overrightarrow{BC} \vert}\]
\[\cos{\gamma} = \dfrac{\overrightarrow{CB} \circ \overrightarrow{CD}}{\vert \overrightarrow{CB} \vert \cdot \vert \overrightarrow{CD} \vert}\]
Verbindungsvektoren \(\overrightarrow{AD}\), \(\overrightarrow{AB}\), \(\overrightarrow{BA}\), \(\overrightarrow{BC}\), \(\overrightarrow{CB}\) und \(\overrightarrow{CD}\) berechnen:
\(A(8|2|0)\), \(B(4|7|6)\), \(C(0|4|6)\), \(D(0|0|3)\)
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 8 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} -8 \\ -2 \\ 3 \end{pmatrix}\]
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 4 \\ 7 \\ 6 \end{pmatrix} - \begin{pmatrix} 8 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} -4 \\ 5 \\ 6 \end{pmatrix}\]
\[\overrightarrow{BA} = -\overrightarrow{AB} = \begin{pmatrix} 4 \\ -5 \\ -6 \end{pmatrix}\]
\[\overrightarrow{BC} = \overrightarrow{C} - \overrightarrow{B} = \begin{pmatrix} 0 \\ 4 \\ 6 \end{pmatrix} - \begin{pmatrix} 4 \\ 7 \\ 6 \end{pmatrix} = \begin{pmatrix} -4 \\ -3 \\ 0 \end{pmatrix}\]
\[\overrightarrow{CB} = -\overrightarrow{BC} = \begin{pmatrix} 4 \\ 3 \\ 0 \end{pmatrix}\]
\[\overrightarrow{CD} = \overrightarrow{D} - \overrightarrow{C} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 0 \\ 4 \\ 6 \end{pmatrix} = \begin{pmatrix} 0 \\ -4 \\ -3 \end{pmatrix}\]
Innenwinkel \(\alpha\), \(\beta\), \(\gamma\) und \(\delta\) berechnen:
\[\begin{align*}\cos{\alpha} &= \frac{\overrightarrow{AD} \circ \overrightarrow{AB}}{\vert \overrightarrow{AD} \vert \cdot \vert \overrightarrow{AB} \vert} \\[0.8em] &= \frac{\begin{pmatrix} -8 \\ -2 \\ 3 \end{pmatrix} \circ \begin{pmatrix} -4 \\ 5 \\ 6 \end{pmatrix}}{\left| \begin{pmatrix} -8 \\ -2 \\ 3 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -4 \\ 5 \\ 6 \end{pmatrix} \right|} \\[0.8em] &= \frac{(-8) \cdot (-4) + (-2) \cdot 5 + 3 \cdot 6}{\sqrt{(-8)^{2} + (-2)^{2} + 3^{2}} \cdot \sqrt{(-4)^{2} + 5^{2} + 6^{2}}} \\[0.8em] &= \frac{40}{\sqrt{77} \cdot \sqrt{77}} \\[0.8em] &= \frac{40}{77} \end{align*}\]
\[\Longrightarrow \quad \alpha \approx 58{,}7^{\circ}\]
\[\begin{align*}\cos{\beta} &= \frac{\overrightarrow{BA} \circ \overrightarrow{BC}}{\vert \overrightarrow{BA} \vert \cdot \vert \overrightarrow{BC} \vert} \\[0.8em] &= \frac{\begin{pmatrix} 4 \\ -5 \\ -6 \end{pmatrix} \circ \begin{pmatrix} -4 \\ -3 \\ 0 \end{pmatrix}}{\left| \begin{pmatrix} 4 \\ -5 \\ -6 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -4 \\ -3 \\ 0 \end{pmatrix} \right|} \\[0.8em] &= \frac{4 \cdot (-4) + (-5) \cdot (-3) + (-6) \cdot 0}{\sqrt{4^{2} + (-5)^{2} + (-6)^{2}} \cdot \sqrt{(-4)^{2} + (-3)^{2} + 0^{2}}} \\[0.8em] &= \frac{-1}{\sqrt{77} \cdot 5} \\[0.8em] &\approx -0{,}02279... \end{align*}\]
\[\Longrightarrow \quad \beta \approx 91{,}3^{\circ}\]
\[\begin{align*}\cos{\gamma} &= \frac{\overrightarrow{CB} \circ \overrightarrow{CD}}{\vert \overrightarrow{CB} \vert \cdot \vert \overrightarrow{CD} \vert} \\[0.8em] &= \frac{\begin{pmatrix} 4 \\ 3 \\ 0 \end{pmatrix} \circ \begin{pmatrix} 0 \\ -4 \\ -3 \end{pmatrix}}{\left| \begin{pmatrix} 4 \\ 3 \\ 0 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ -4 \\ -3 \end{pmatrix} \right|} \\[0.8em] &= \frac{4 \cdot 0 + 3 \cdot (-4) + 0 \cdot (-3)}{\sqrt{4^{2} + 3^{2} + 0^{2}} \cdot \sqrt{0^{2} + (-4)^{2} + (-3)^{2}}} \\[0.8em] &= \frac{-12}{5 \cdot 5} \\[0.8em] &= -\frac{12}{25} \end{align*}\]
\[\Longrightarrow \quad \gamma \approx 118{,}7^{\circ}\]
\[\begin{align*}\delta &= 360^{\circ} - (\alpha + \beta + \gamma) \\[0.8em] &= 360^{\circ} - (58{,}7^{\circ} + 91{,}3^{\circ} + 118{,}7^{\circ}) \\[0.8em] &= 360^{\circ} - 268{,}7^{\circ} \\[0.8em] &= 91{,}3^{\circ} \end{align*}\]
Schlussfolgerung:
\[\left. \begin{align*} &[AC] \perp [BD] \\[0.8em] &\beta = \delta \\[0.8em] &\alpha \neq \gamma \end{align*} \right\} \enspace \Rightarrow \enspace \text{Drachenviereck}\; ABCD\]


