Bestimmen Sie die momentane Änderungsrate des Flächeninhalts des Algenteppichs zu Beobachtungsbeginn.
(4 BE)
Lösung zu Teilaufgabe 2c
\[A(x) = \frac{8}{f(x)}; \; D_{A} = \mathbb R_{0}^{+}\]
\[f(x) = 1 + 7e^{-0{,}2x}; \; D_{f} = \mathbb R_{0}^{+}\]
Differentialquotient oder lokale bzw. momentane Änderungsrate
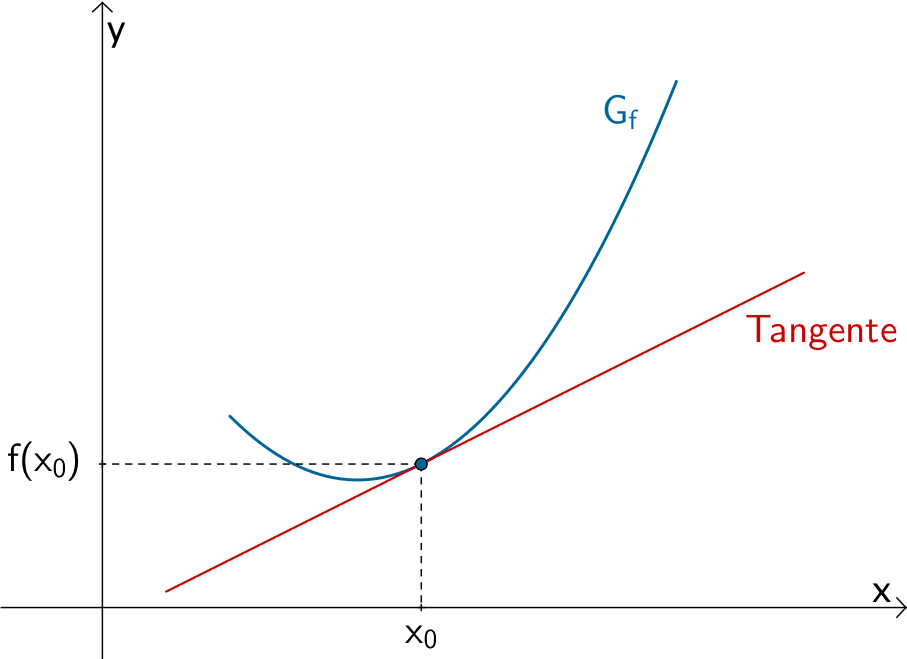
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Es ist \(A'(0)\) zu berechnen.
Erste Ableitung \(A'(x)\) bilden:
Der Funktionsterm \(A(x)\) lässt sich zeitsparend unter Berücksichtigung des in Teilaufgabe 1a ermittelten Ergebnisses für \(f'(x)\) und mithilfe der Quotientenregel ableiten. Als Alternative kann \(A(x)\) nach einer Umformulierung in die Potenzschreibweise (\(\frac{1}{a^{n}} = a^{-n}\)) mithilfe der Kettenregel abgeleitet werden.
1. Möglichkeit: Quotientenregel anwenden
\[A(x) = \frac{\textcolor{#0087c1}{8}}{\textcolor{#cc071e}{f(x)}}; \; D_{A} = \mathbb R_{0}^{+}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*} A'(x) & = \frac{\textcolor{#0087c1}{0} \cdot \textcolor{#cc071e}{f(x)} - \textcolor{#0087c1}{8} \cdot \textcolor{#cc071e}{f'(x)}}{\left[ \textcolor{#cc071e}{f(x)} \right]^{2}} &&| \, f'(x) = -1{,}4e^{-0{,}2x}\; \text{(vgl. Teilaufgabe 1a)} \\[0.8em] &= \frac{(-8) \cdot \left( -1{,}4e^{-0{,}2x} \right)}{\left( 1 + 7e^{-0{,}2x} \right)^{2}} \\[0.8em] &= \frac{11{,}2e^{-0{,}2x}}{\left( 1 + 7e^{-0{,}2x} \right)^{2}} \end{align*}\]
Oder ohne Berücksichtigung des Ergebnisses für \(f'(x)\) aus Teilaufgabe 1a:
\[A(x) = \frac{\textcolor{#0087c1}{8}}{\textcolor{#cc071e}{1 + 7e^{-0{,}2x}}}; \; D_{A} = \mathbb R_{0}^{+}\]
\[\begin{align*} A'(x) &= \frac{\textcolor{#0087c1}{0} \cdot \textcolor{#cc071e}{\left( 1 + 7e^{-0{,}2x} \right)} - \textcolor{#0087c1}{8} \cdot \textcolor{#cc071e}{\big( 0 + 7}\overbrace{\textcolor{#cc071e}{e^{-0{,}2x} \cdot (-0{,}2)}}^{\text{Kettenregel}} \textcolor{#cc071e}{\big)}}{\left( \textcolor{#cc071e}{1 + 7e^{-0{,}2x}} \right)^{2}} \\[0.8em] &= \frac{(-8) \cdot \left( -1{,}4e^{-0{,}2x} \right)}{\left( 1 + 7e^{-0{,}2x} \right)^{2}} \\[0.8em] &= \frac{11{,}2e^{-0{,}2x}}{\left( 1 + 7e^{-0{,}2x} \right)^{2}}\end{align*}\]
2. Möglichkeit: Mit der Kettenregel (nach Umformulierung in die Potenzschreibweise)
\[A(x) = \frac{8}{f(x)} = 8 \cdot \textcolor{#0087c1}{(}\textcolor{#cc071e}{f(x)}\textcolor{#0087c1}{)^{-1}}; \; D_{A} = \mathbb R_{0}^{+}\]
\[\begin{align*} A'(x) &= 8 \cdot \overbrace{\textcolor{#0087c1}{(-1)} \cdot \textcolor{#0087c1}{(}\textcolor{#cc071e}{f(x)}\textcolor{#0087c1}{)^{-2}} \cdot \textcolor{#cc071e}{f'(x)}}^{\text{Kettenregel}} &&| \, a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{(-8) \cdot f'(x)}{(f(x))^{2}} &&| \, f'(x) = -1{,}4e^{-0{,}2x}\;\text{(vgl. Teilaufgabe 1a)} \\[0.8em] &= \frac{(-8) \cdot \left( -1{,}4e^{-0{,}2x} \right)}{\left( 1 + 7e^{-0{,}2x} \right)^{2}} \\[0.8em] &= \frac{11{,}2e^{-0{,}2x}}{\left( 1 + 7e^{-0{,}2x} \right)^{2}} \end{align*}\]
Oder ohne Berücksichtigung des Ergebnisses für \(f'(x)\) aus Teilaufgabe 1a:
\[A(x) = \frac{8}{f(x)} = 8 \cdot \textcolor{#0087c1}{(}\textcolor{#cc071e}{1 + 7e^{0{,}2x}}\textcolor{#0087c1}{)^{-1}}; \; D_{A} = \mathbb R_{0}^{+}\]
\[\begin{align*} A'(x) &= 8 \cdot \overbrace{\textcolor{#0087c1}{(-1)} \cdot \textcolor{#0087c1}{(}\textcolor{#cc071e}{1 + 7e^{-0{,}2x}} \textcolor{#0087c1}{)^{-2}} \cdot \textcolor{#cc071e}{(0 + 7}\overbrace{\textcolor{#cc071e}{e^{-0{,}2x}} \cdot \textcolor{#cc071e}{(-0{,}2)}}^{\text{Kettenregel}} \textcolor{#cc071e}{)}}^{\text{Kettenregel}} \\[0.8em] &= (-8) \cdot \left( 1 + 7e^{-0{,}2x} \right)^{-2} \cdot \left( -1{,}4e^{-0{,}2x} \right) &&| \, a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{11{,}2e^{-0{,}2x}}{\left( 1 + 7e^{-0{,}2x} \right)^{2}}\end{align*}\]
\(A'(0)\) berechnen:
\[A'(\textcolor{#e9b509}{0}) = \frac{11{,}2\overbrace{e^{-0{,}2 \cdot \textcolor{#e9b509}{0}}}^{1}}{\big( 1 + 7\underbrace{e^{-0{,}2 \cdot \textcolor{#e9b509}{0}}}_{1} \big)^{2}} = \frac{11{,}2}{8^{2}} = 0{,}175\]
Zu Beobachtungsbeginn beträgt die momentane Änderungsrate des Algenteppichs am Südufer des Sees \(\sf{0{,}175} \frac{\sf{m^{2}}}{\sf{Tag}}\).


