- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(g \colon x \mapsto \ln{(2 - x^{2})}\) mit maximaler Definitionsmenge \(D_{g}\).
Skizzieren Sie die Parabel mit der Gleichung \(y = 2 - x^{2}\) in einem Koordinatensystem und geben Sie \(D_{g}\) an.
(3 BE)
- Details
- Kategorie: Analysis 2
Ermitteln Sie den Term der Ableitungsfunktion \(g'\) von \(g\).
(2 BE)
- Details
- Kategorie: Analysis 2
Die Abbildung 1 zeigt einen Teil des Graphen \(G_{h}\) einer in \(\mathbb R \backslash \{2\}\) definierten gebrochenrationalen Funktion \(h\). Die Funktion \(h\) hat bei \(x = 2\) eine Polstelle ohne Vorzeichenwechsel; zudem besitzt \(G_{h}\) die Gerade mit der Gleichung \(y = x - 7\) als schräge Asymptote.
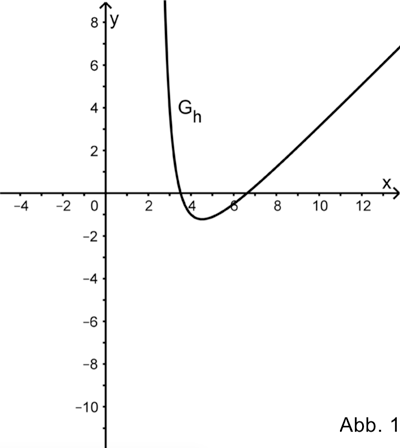
Zeichnen Sie in die Abbildung 1 die Asymptoten von \(G_{h}\) ein und skizzieren Sie im Bereich \(x < 2\) einen möglichen Verlauf von \(G_{h}\).
(3 BE)
- Details
- Kategorie: Analysis 2
Berechnen Sie unter Berücksichtigung des asymptotischen Verhaltens von \(G_{h}\) einen Näherungswert für \(\displaystyle \int_{10}^{20} h(x)dx\).
(2 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(k \colon x \mapsto \dfrac{-x^{2} + 2x}{2x^{2} + 4}\). Ihr Graph wird mit \(G_{k}\) bezeichnet.
Geben Sie die Nullstellen von \(k\) an und begründen Sie anhand des Funktionsterms, dass \(G_{k}\) die Gerade mit der Gleichung \(y = -0{,}5\) als waagrechte Asymptote besitzt.
(3 BE)
- Details
- Kategorie: Analysis 2
Berechnen Sie die \(x\)-Koordinate des Schnittpunkts von \(G_{k}\) mit der waagrechten Asymptote.
(2 BE)
- Details
- Kategorie: Analysis 2
Die Abbildung 2 zeigt den Graphen \(G_{f}\) einer in \([0{,}8; +\infty[\) definierten Funktion f.
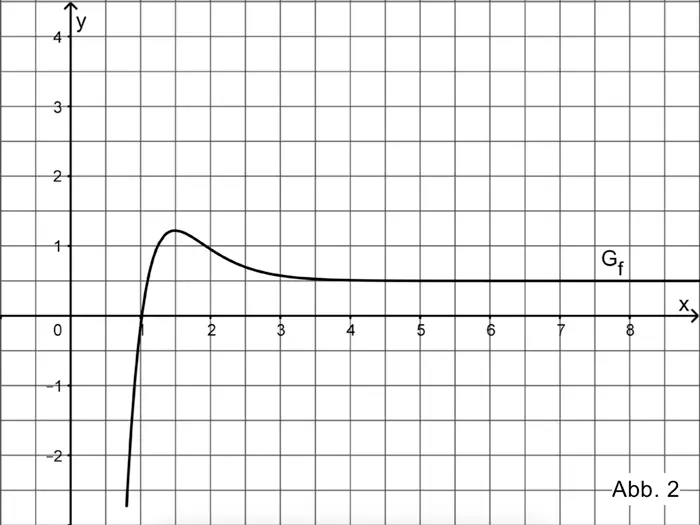
Betrachtet wird zudem die in \([0{,}8; +\infty[\) definierte Integralfunktion \(\displaystyle J \colon x \mapsto \int_{2}^{x} f(t) dt\).
Begründen Sie mithilfe von Abbildung 2, dass \(J(1) \approx -1\) gilt, und geben Sie einen Näherungswert für den Funktionswert \(J(4{,}5)\) an. Skizzieren Sie den Graphen von \(J\) in der Abbildung 2.
(5 BE)


