Skizzieren des Graphen einer Integralfunktion

Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(R\) definierten Funktion \(f\).

a) Skizzieren Sie den Graphen \(G_{F}\) der Integralfunktion \(F \colon x \mapsto \displaystyle \int_{0}^{x} f(t) dt\) in die Abbildung. Gehen Sie dabei insbesondere auf die Nullstellen und die Extremstelle von \(G_{f}\) sowie auf das Verhalten von \(G_{f}\) für \(x \to \pm \infty\) ein. Erläutern Sie Ihre Vorgehensweise.

b) „Jede Stammfunktion der abgebildeten Funktion \(f\) ist eine Integralfunktion." Nehmen Sie zu dieser Aussage begründend Stellung, indem Sie sich auf \(G_{F}\) beziehen.

Die Abbildung 2 zeigt den Graphen \(G_{f}\) einer in \([0{,}8; +\infty[\) definierten Funktion f.

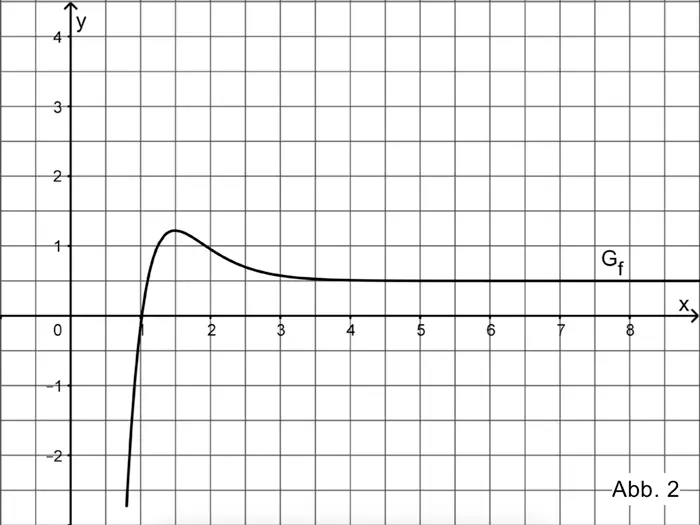
Betrachtet wird zudem die in \([0{,}8; +\infty[\) definierte Integralfunktion \(\displaystyle J \colon x \mapsto \int_{2}^{x} f(t) dt\).

Begründen Sie mithilfe von Abbildung 2, dass \(J(1) \approx -1\) gilt, und geben Sie einen Näherungswert für den Funktionswert \(J(4{,}5)\) an. Skizzieren Sie den Graphen von \(J\) in der Abbildung 2.

(5 BE)