Um einen Näherungswert für die Länge der oberen Profillinie der Vorderseite der Dachgaube berechnen zu können, wird \(G_f\) im Bereich \(-4 \leq x \leq 4\) durch vier Kreisbögen angenähert, die nahtlos ineinander übergehen und zueinander kongruent sind. Einer dieser Kreisbögen erstreckt sich im Bereich \(0 \leq x \leq 2\) und ist Teil des Kreises mit Mittelpunkt \(M(0|-1)\) und Radius 3. Berechnen Sie den Mittelpunktswinkel des zu diesem Kreisbogen gehörenden Kreissektors und ermitteln Sie damit den gesuchten Näherungswert.
(5 BE)
Lösung zu Teilaufgabe 2e
Mittelpunktswinkel: \(\sin{\alpha} = \dfrac{2}{3} \; \Rightarrow \; \alpha \approx 41{,}8^{\circ}\)
Näherungswert für die Länge der oberen Profillinie:
\[4 \cdot \frac{41{,}8^{\circ}}{360^{\circ}} \cdot 2 \cdot 3 \cdot \pi \approx 8{,}76\]
Die Länge der oberen Profillinie beträgt ungefähr 8,76 m.
Ausführliche Lösung (nicht verlangt)
Berechnung des Mittelpunktswinkels
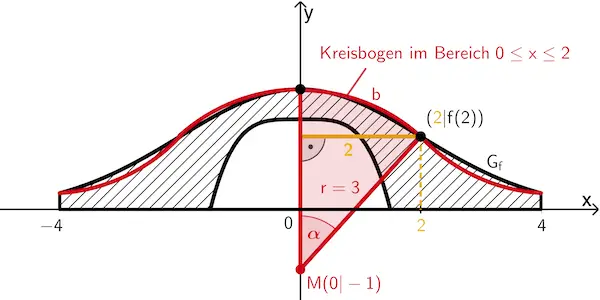
Planskizze (optional): Der Kreisbogen im Bereich \(\textcolor{#cc071e}{0 \leq x \leq 2}\) der Länge \(\textcolor{#cc071e}{b}\) verläuft von Punkt \((\textcolor{#e9b509}{2}|f(2))\) zum Schnittpunkt von \(G_f\) mit der \(y\)-Achse. Der zugehörige Kreissektor hat den Mittelpunktswinkel \(\textcolor{#cc071e}{\alpha}\) und den Radius \(\textcolor{#cc071e}{r = 3}\).
Es lässt sich ein rechtwinkliges Dreieck konstruieren, in dem der Radius des Kreissektors die Hypotenuse ist und die \(\textcolor{#e9b509}{x}\)-Koordinate des Punktes \((\textcolor{#e9b509}{2}|f(2))\) der Länge der Gegekathete bezüglich des Mittelpunktswinkels \(\alpha\) entspricht.
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
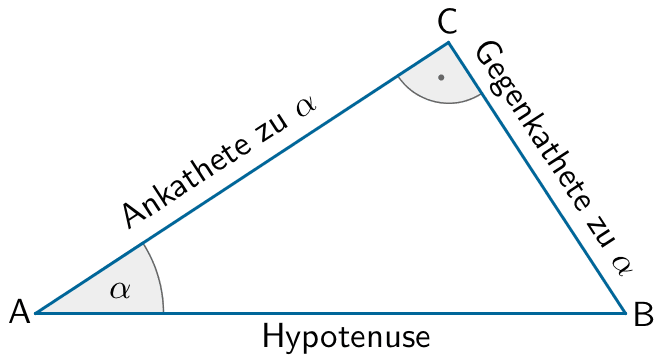
\[\begin{align*}\sin{\textcolor{#cc071e}{\alpha}} &= \frac{\textcolor{#e9b509}{\text{Gegenkathete}}}{\textcolor{#cc071e}{\text{Hypotenuse}}} = \frac{\textcolor{#e9b509}{2}}{\textcolor{#cc071e}{3}} &&| \; \text{TR:}\; \sin^{-1}\left( \frac{2}{3}\right) \\[0.8em] \textcolor{#cc071e}{\alpha}\; &\textcolor{#cc071e}{\approx 41{,}8^{\circ}}\end{align*}\]
Berechnung des Näherungswerts für die Länge der oberen Profillinie
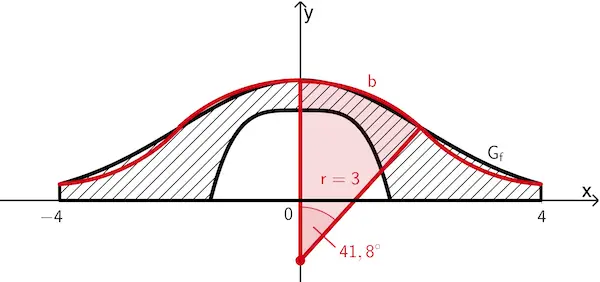
Der Verlauf von \(G_f\) wird im Bereich \(-4 \leq x \leq 4\) durch vier Kreisbögen der Länge \(\textcolor{#cc071e}{b}\) angenähert. Für die Berechnung der Kreisbogenlänge \(\textcolor{#cc071e}{b}\) wird der Mittelpunktswinkel \(\textcolor{#cc071e}{\alpha}\) sowie der Radius \(\textcolor{#cc071e}{r}\) des zugehörigen Kreissektors benötigt.
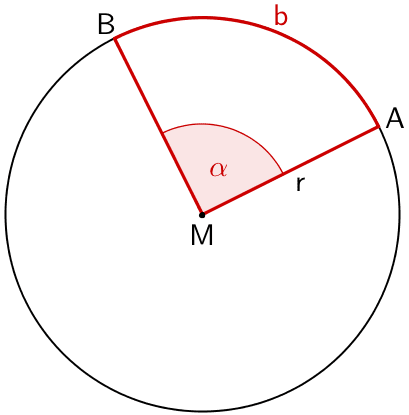
Länge eines Kreisbogens
\[b = \frac{\alpha}{360^{\circ}} \cdot u = \frac{\alpha}{360^{\circ}} \cdot 2 \cdot r \cdot \pi\]
\[4 \cdot \textcolor{#cc071e}{b} = 4 \cdot \frac{\textcolor{#cc071e}{\alpha}}{360^{\circ}} \cdot 2 \cdot \textcolor{#cc071e}{r} \cdot \pi = 4 \cdot \frac{\textcolor{#cc071e}{41{,}8^{\circ}}}{360^{\circ}} \cdot 2 \cdot \textcolor{#cc071e}{3} \cdot \pi \approx 8{,}76\]
Die Länge der oberen Profillinie beträgt ungefähr 8,76 m.


