Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl \((Z)\) oder zum zweiten Mal Wappen \((W)\) oben liegt. Als Ergebnismenge wird festgelegt: \(\{ZZ; WW; ZWZ; ZWW; WZZ; WZW\}\).
Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.
(2 BE)
Lösung zu Teilaufgabe 1a
Mehrstufiges Zufallsexperiment, Laplace-Experiment
\(Z\): Zahl
\(W\): Wappen
\[\Omega = \{ZZ; WW; ZWZ;ZWW;WZZ;WZW\}\]
Ein Laplace-Experiment liegt dann vor, wenn alle möglichen Ergebnisse (alle möglichen Versuchsausgänge) des Zufallsexperiments gleichwahrscheinlich sind.
Die Angabe nennt den Ergebnisraum \(\Omega\) des Zufallsexperiments. Es ist folglich nachzuweisen, dass die Wahrscheinlichkeiten für das Eintreten der Ergebnisse von \(\Omega\) nicht gleichwahrscheinlich sind.
Ein Baumdiagramm des Zufallsexperiments gibt einen Überblick für die zu berechnenden Wahrscheinlichkeiten.
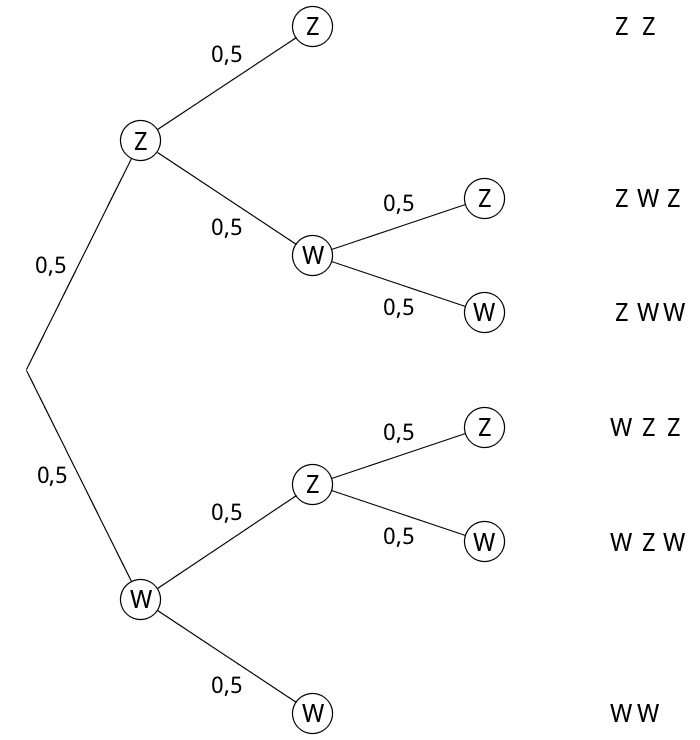
Baumdiagramm des mehrstufigen Zufallsexperiments: „Eine ideale Münze wird so lange geworfen, bis zum zweiten Mal Zahl \(Z\) oder zum zweiten Mal Wappen \(W\) oben liegt." Die Ereignisse \(Z\) und \(W\) treten beim Werfen der idealen Münze jeweils mit der Wahrscheinlichkeit 0,5 ein.
Berechnung der Wahrscheinlichkeiten der Ergebnisse des Zufallsexperiments:
\[P(\{ZZ\}) = P(\{WW\}) = 0{,}5 \cdot 0{,}5 = 0{,}25\]
\[\begin{align*}P(\{ZWZ\}) &= P(\{ZWW\}) = P(\{WZZ\}) = P(\{WZW\}) \\[0.8em] &= 0{,}5 \cdot 0{,}5 \cdot 0{,}5 \\[0.8em] &= 0{,}125\end{align*}\]
Schlussfolgerung:
Die Ergebnisse des Ergebnisraums \(\Omega = \{ZZ; WW; ZWZ;ZWW;WZZ;WZW\}\) sind nicht gleichwahrscheinlich. Das Zufallsexperiment ist kein Laplace-Experiment.


