Die Abbildung zeigt ein gerades Prisma \(ABCDEF\) mit \(A\,(0|0|0)\), \(B\,(8|0|0)\), \(C\,(0|8|0)\) und \(D\,(0|0|4)\).
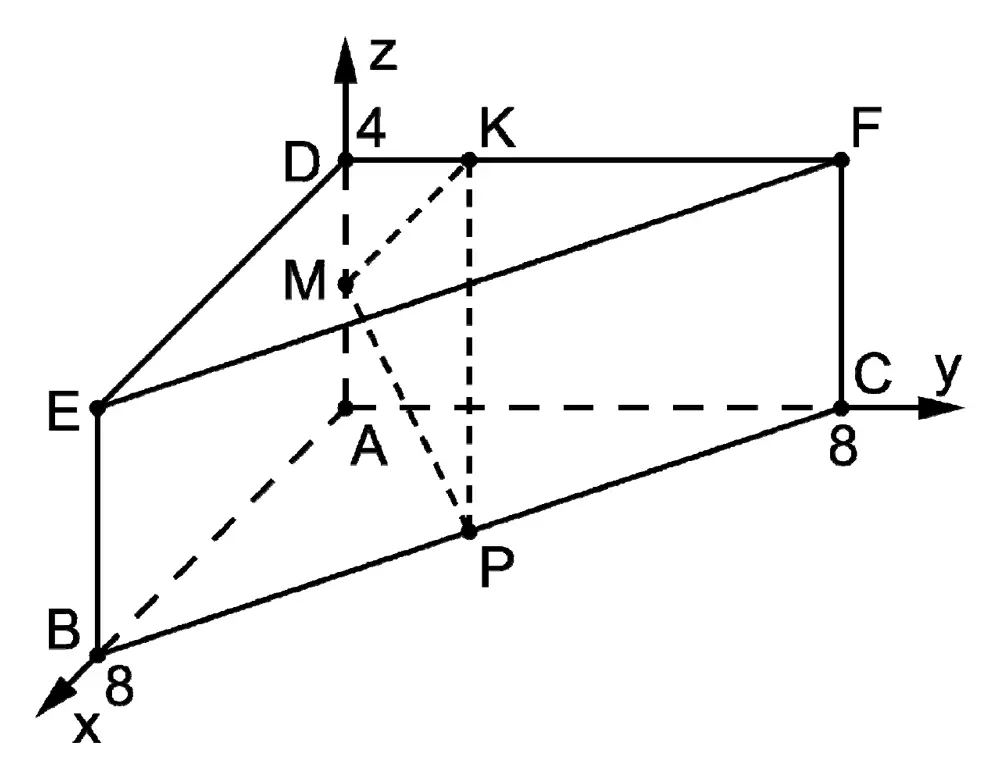
Bestimmen Sie den Abstand der Eckpunkte \(B\) und \(F\).
(2 BE)
Lösung zu Teilaufgabe 1a
\[A\,(0|0|0)\,, \enspace B\,(8|0|0)\,, \enspace C\,(0|8|0)\,, \enspace D\,(0|0|4)\]
Der Abbildung entnimmt man die Koordinaten des Punktes \(F\) oder bestimmt den Ortsvektor \(\overrightarrow{F}\) durch Vektoraddition.
Da es sich um ein gerades Prisma handelt, besitzt der Punkt \(F\) die gleiche \(x_1\)- und \(x_2\)-Koordinate wie Punkt \(C\) und die gleiche \(x_3\)-Koordinate wie Punkt \(D\).
\(\Longrightarrow \quad F\,(0|8|4)\)
\[\overrightarrow{F} = \overrightarrow{AC} + \overrightarrow{CF} = \overrightarrow{C} + \overrightarrow{D} = \begin{pmatrix} 0 \\ 8 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix} 0 \\ 8 \\ 4 \end{pmatrix}\]
Abstand der Eckpunkte \(B\) und \(F\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d\,(B;F) &= \vert \overrightarrow{BF} \vert \\[0.8em] &= \vert \overrightarrow{F} - \overrightarrow{B} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 8 \\ 4 \end{pmatrix} - \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -8 \\ 8 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-8)^2 + 8^2 + 4^2} \\[0.8em] &= \sqrt{64 + 64 + 16} \\[0.8em] &= \sqrt{144} \\[0.8em] &= 12 \end{align*}\]


