Es gibt Tangenten an den Graphen von \(f\), die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermitteln Sie anhand des Graphen \(\mathbf{G_{f'}}\) der Ableitungsfunktion \(f'\) in der Abbildung 1 Näherungswerte für die \(x\)-Koordinaten derjenigen Punkte, in denen der Graph von \(f\) jeweils eine solche Tangente hat.
(2 BE)
Lösung zu Teilaufgabe 2b
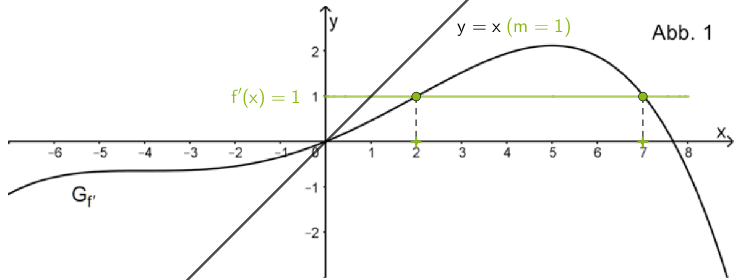
Die Gleichung der Winkelhalbierenden des I. und III. Quadranten lautet \(y = x\). Sie hat die Steigung \(m = 1\).
Zu dieser Winkelhalbierenden parallele Tangenten an den Graphen von \(f\) haben ebenfalls die Steigung 1.
Da die erste Ableitung \(f'\) die Steigung einer Tangente an den Graphen von \(f\) beschreibt, muss gelten:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[f'(x) = 1\]
In Abbildung 1 schneidet die Gerade \(y = 1\) (f'(x) = 1) den Graphen \(G_{f'}\) an den Stellen \(x_{1} \approx 2\) und \(x_{2} \approx 7\). An diesen Stellen verlaufen die Tangenten an \(G_{f}\) parallel zur Winkelhalbierenden des I. und III. Quadranten.


