Berechnen Sie die Größe \(\varphi\) des Winkels, unter dem \(E\) die \(x_1x_2\)-Ebene schneidet. Geben Sie einen Term an, mit dem aus \(\varphi\) die Größe des Winkels zwischen den Ebenen \(E\) und \(F\) berechnet werden kann.
(5 BE)
Lösung zu Teilaufgabe d
Größe \(\varphi\) des Winkels, unter dem \(E\) die \(x_1x_2\)-Ebene schneidet
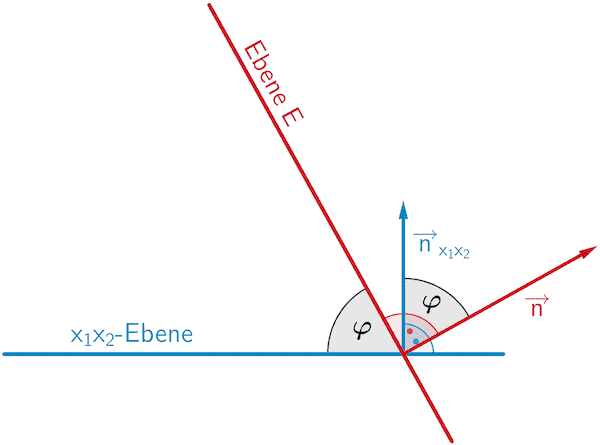
Der Schnittwinkel der Ebene \(\textcolor{#cc071e}{E}\) und der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene ist gleich dem Winkel zwischen den Normalenvektoren der Ebenen (Skizze schematisch, nicht verlangt).
\(\textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}}\) ist ein Normalenvektor der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene.
\(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 14 \\ 14 \\ 11 \end{pmatrix}}\) ist ein Normalenvektor der Ebene \(\textcolor{#cc071e}{E}\) (vgl. Teilaufgabe c).
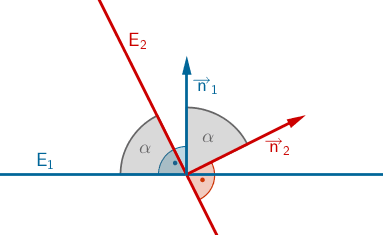
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
\[\begin{align*} \cos{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{n}} \circ \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{n}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert} = \frac{\left| \textcolor{#cc071e}{\begin{pmatrix} 14 \\ 14 \\ 11 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|}{\left| \textcolor{#cc071e}{\begin{pmatrix} 14 \\ 14 \\ 11 \end{pmatrix}} \right| \cdot \left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|} \\[0.8em] &= \frac{\vert \textcolor{#cc071e}{14} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{14} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{11} \cdot \textcolor{#0087c1}{1} \vert}{\sqrt{\textcolor{#cc071e}{14}^2 + \textcolor{#cc071e}{14}^2 + \textcolor{#cc071e}{11}^2} \cdot \sqrt{\textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{1}^2}} \\[0.8em] &= \frac{11}{\sqrt{513}} &&| \; \text{TR:}\; \cos^{-1}(\dots) \\[2.4em] \varphi &= \cos^{-1}\left( \frac{11}{\sqrt{513}} \right) \approx 60{,}9^{\circ}\end{align*}\]
Term, mit dem aus \(\varphi\) die Größe des Winkels zwischen den Ebenen \(E\) und \(F\) berechnet werden kann
\[180^{\circ} - 2\varphi\]
Begründung (nicht verlangt)
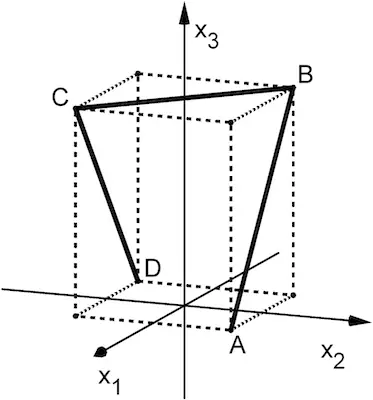
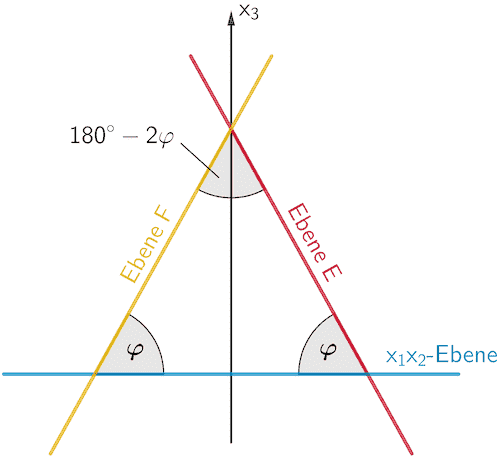
![Der Schnittpunkt der Ebenen E und F mit der x₃-Achse bildet zusammen mit der Basis [AD] ein gleichschenkliges (Stütz)Dreieck](/images/stories/B2022_PT_B_G2/B2022_PT_B_G2_d3.png)
Da sowohl die Ebene \(\textcolor{#cc071e}{E}\) als auch die Ebene \(\textcolor{#e9b509}{F}\) die Punkte \(B\) und \(C\) enthält, ist die Gerade \(BC\) die Schnittgerade beider Ebenen. Die Punkte \(A\) und \(D\) liegen ebenso wie die Punkte \(B\) und \(C\) symmetrisch bezüglich der \(x_3\)-Achse (vgl. Teilaufgabe a).
Damit bildet der Schnittpunkt der Ebenen mit der \(x_3\)-Achse zusammen mit der Basis \([AD]\) ein gleichschenkliges (Stütz)Dreieck mit dem Basiswinkel \(\varphi\).
Die Innenwinkelsumme eines Dreiecks beträgt \(180^{\circ}\). Somit ist \(180^{\circ} - 2\varphi\) ein Term für die Berechnung der Größe des Winkels zwischen den Ebenen \(E\) und \(F\).


