Untersuchen Sie, ob der höchste Punkt der Wasserfontäne höher liegt als der höchste Punkt des Brunnens.
(2 BE)
Lösung zu Teilaufgabe g
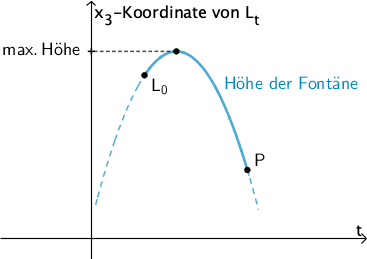
Planskizze (optional): Der quadratische Term \(\textcolor{#0087c1}{6{,}2 - 5 \cdot (t - 0{,}2)^{2}}\) der \(x_{3}\)-Koordinate der Punkte \(\textcolor{#0087c1}{L_{t}}\) beschreibt für geeignete Werte \(t \in \mathbb R_{0}^{+}\) die Höhe der Wasserfontäne. Der zugehörige Graph ist eine nach unten geöffnete Parabel, deren höchster Punkt der Scheitelpunkt ist.
1. Möglichkeit: Wert des quadratischen Terms \(6{,}2 - 5 \cdot (t - 0{,}2)^{2}\) für \(t \geq 0\) beurteilen
\[6{,}2 - 5 \cdot \underbrace{(t - 0{,}2)^{2}}_{\geq 0}\textcolor{#0087c1}{\leq 6{,}2}\]
Für \(t \geq 0\) nimmt der quadratische Term \(6{,}2 - 5 \cdot (t - 0{,}2)^{2}\) höchstens den Wert \(6{,}2\) an (6,2 dm, vgl. Angabe). Dies entspricht einer maximalen Höhe der Wasserfontäne von 62 cm. Der Höchste Punkt der Wasserfontäne liegt damit niedriger als der höchste Punkt des Brunnens (64 cm, vgl. Teilaufgabe e).
2. Möglichkeit: Scheitelpunktform einer quadratischen Funktion
Dem Quadratischen Term \(6{,}2 - 5 \cdot (t - 0{,}2)^{2}\) kann der Scheitelpunkt der zugehörigen nach unten geöffneten Parabel direkt entnommen werden:
Quadratische Funktion:
\[f(x) = ax^2 + bx + c\,; \quad a, b, c \, \in \, \mathbb R\,, a \neq 0\]
Scheitelpunktform
\[f(x) = a(x - d)^2 + e\]
Scheitelpunkt
\[S\,(d|e) \qquad d = -\frac{b}{2a}\,; \quad e = c - \frac{b^2}{4a}\]
\[6{,}2 - 5 \cdot (t - 0{,}2)^{2} = -5 \cdot (t - \textcolor{#e9b509}{0{,}2})^{2} + \textcolor{#0087c1}{6{,}2} \enspace \Rightarrow \enspace S(\textcolor{#e9b509}{0{,}2}|\textcolor{#0087c1}{6{,}2})\]
Die \(y\)-Koordinate des Scheitelpunkts \(S\) entspricht mit \(\textcolor{#0087c1}{6{,}2}\) einer maximalen Höhe der Wasserfontäne von 62 cm. Der Höchste Punkt der Wasserfontäne liegt damit niedriger als der höchste Punkt des Brunnens (64 cm, vgl. Teilaufgabe e).

