Die Funktion \(k\) besitzt die Periode \(\pi\).
(1 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = \sin x\,; \quad D = \mathbb R\]
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
Die Funktion \(x \mapsto \sin x\) besitzt die Periode \(2\pi\). Demnach muss die Funktion \(k\) in \(x\)-Richtung um den Faktor 2 gestaucht bzw. um den Faktor \(\frac{\sf{1}}{\sf{2}}\) gestreckt sein.
\[\Longrightarrow \quad k(x) = f(2x) = \sin(2x)\,; \quad D = \mathbb R\]
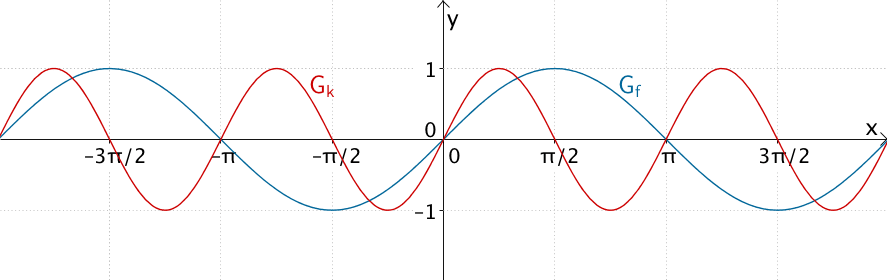
Graph der Sinusfunktion \(f\,\colon x \mapsto \sin x\) und Graph der Funktion \(k\)


