Das Spatprodukt ist ein aus drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) gebildetes gemischtes Produkt aus Skalar- und Vektorprodukt. Das Ergebnis ist eine reelle Zahl.
Spatprodukt
Unter dem Spatprodukt dreier Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) versteht man das skalare Produkt aus einem der Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) und dem aus den beiden anderen Vektoren gebildeten Vektorprodukt.
\(\overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c})\) (Beispiel)
Berechnung eines Spatprodukts (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren und Abiturskript - 2.1.4 Vektorprodukt):
\[\begin{align*}\overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c}) \enspace = \qquad &\begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_2 \cdot c_3 - b_3 \cdot c_2 \\ b_3 \cdot c_1 - b_1 \cdot c_3 \\ b_1 \cdot c_2 - b_2 \cdot c_1 \end{pmatrix} \\[0.8em] = \qquad & \; a_{1} \cdot (b_2 \cdot c_3 - b_3 \cdot c_2) \\[0.8em] + \enspace & \; a_{2} \cdot (b_3 \cdot c_1 - b_1 \cdot c_3) \\[0.8em] + \enspace & \; a_{3} \cdot (b_1 \cdot c_2 - b_2 \cdot c_1)\end{align*}\]
Anwendungen des Spatprodukts
Mithilfe des Spatprodukts lässt sich das Volumen eines von drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) aufgespannten Spats berechnen.
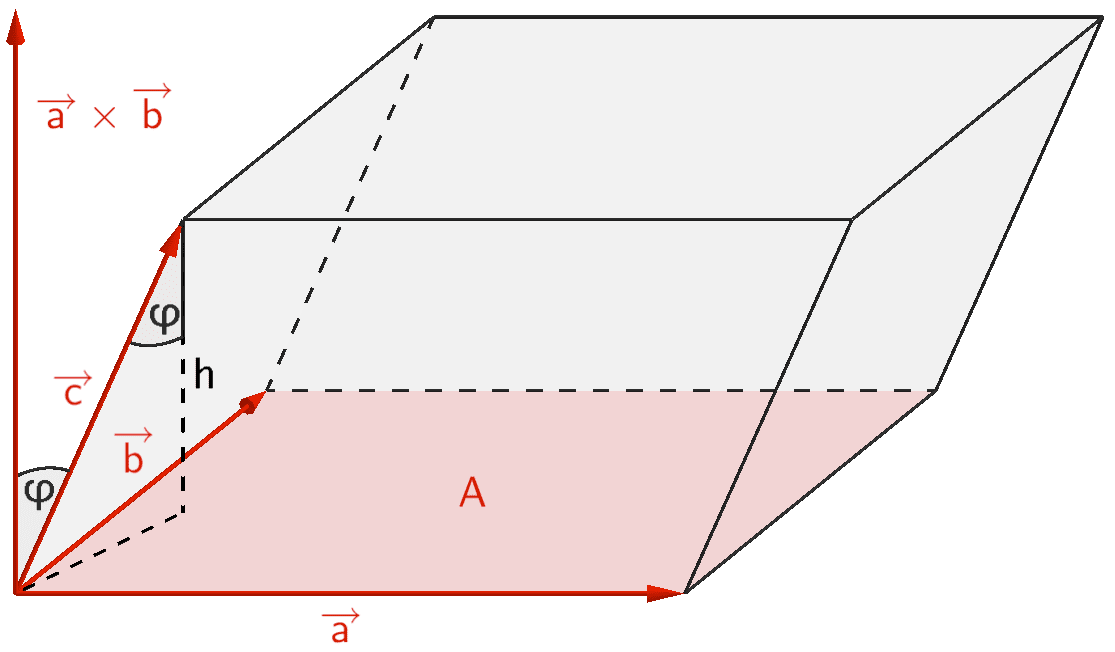
\[\begin{align*} V_{\text{Spat}} &= A \cdot h \\[0.8em] &= \vert \overrightarrow{a} \times \overrightarrow{b} \vert \cdot \vert \overrightarrow{c} \vert \cdot \cos{\varphi} \\[0.8em] &= (\overrightarrow{a} \times \overrightarrow{b}) \circ \overrightarrow{c} \end{align*}\]
(vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren und Abiturskript - 2.1.4 Vektorprodukt, Anwendungen)
Wählt man für die Berechnung des Volumen eines Spats den Betrag des Spatprodukts, spielt die Reihenfolge der Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) keine Rolle.
Volumen eines Spats (vgl. Merkhilfe)
\[V_{\text{Spat}} = \vert \overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c}) \vert\]
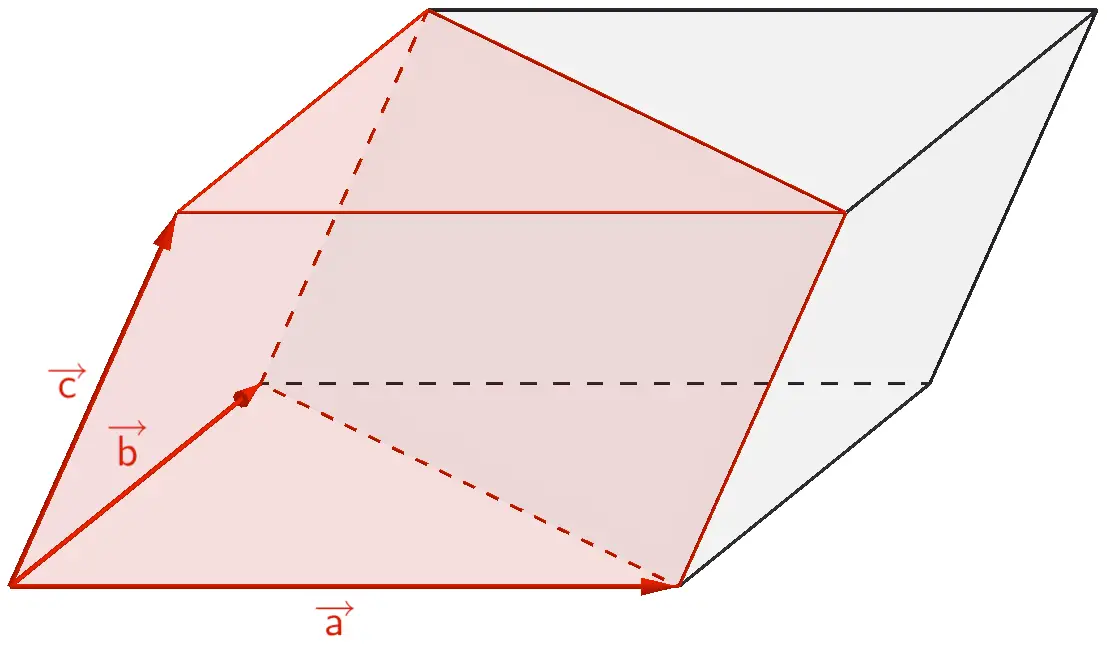
Der Spat lässt sich in zwei volumengleiche Prismen zerlegen.
\[\begin{align*}V_{\text{Prisma}} &= \frac{1}{2} \cdot V_{\text{Spat}} \\[0.8em] &= \frac{1}{2} \cdot \vert \overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c}) \vert \end{align*}\]
Die von den Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) aufgespannte dreiseitige Pyramide nimmt ein Drittel des Volumens eines Prismas ein. Somit beträgt das Volumen der dreiseitigen Pyramide ein Sechstel des Spatvolumens.
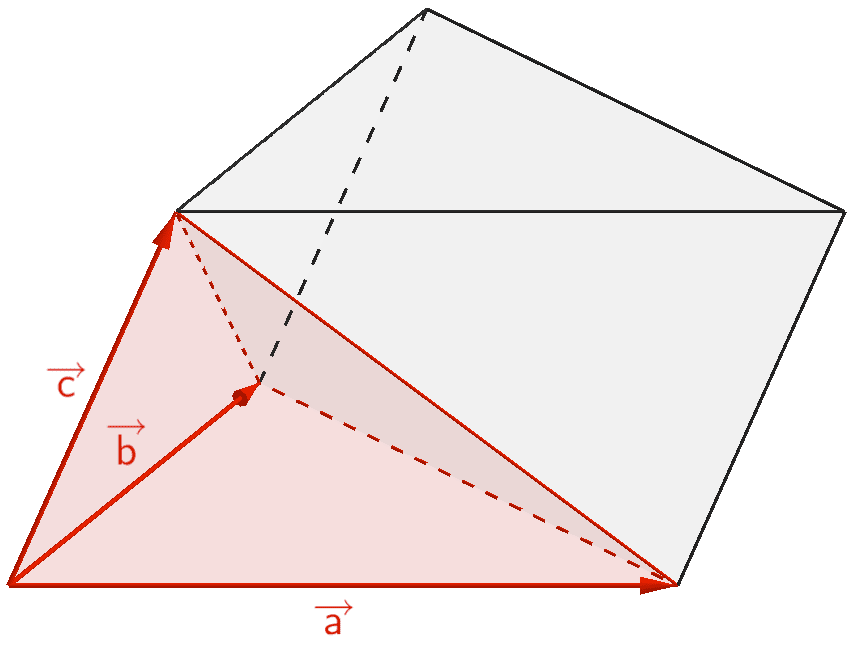
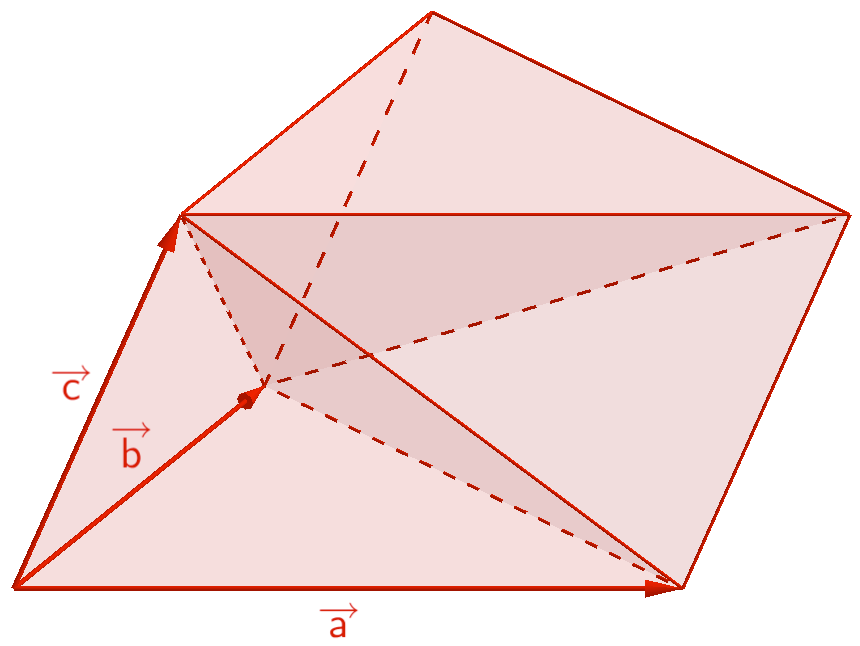
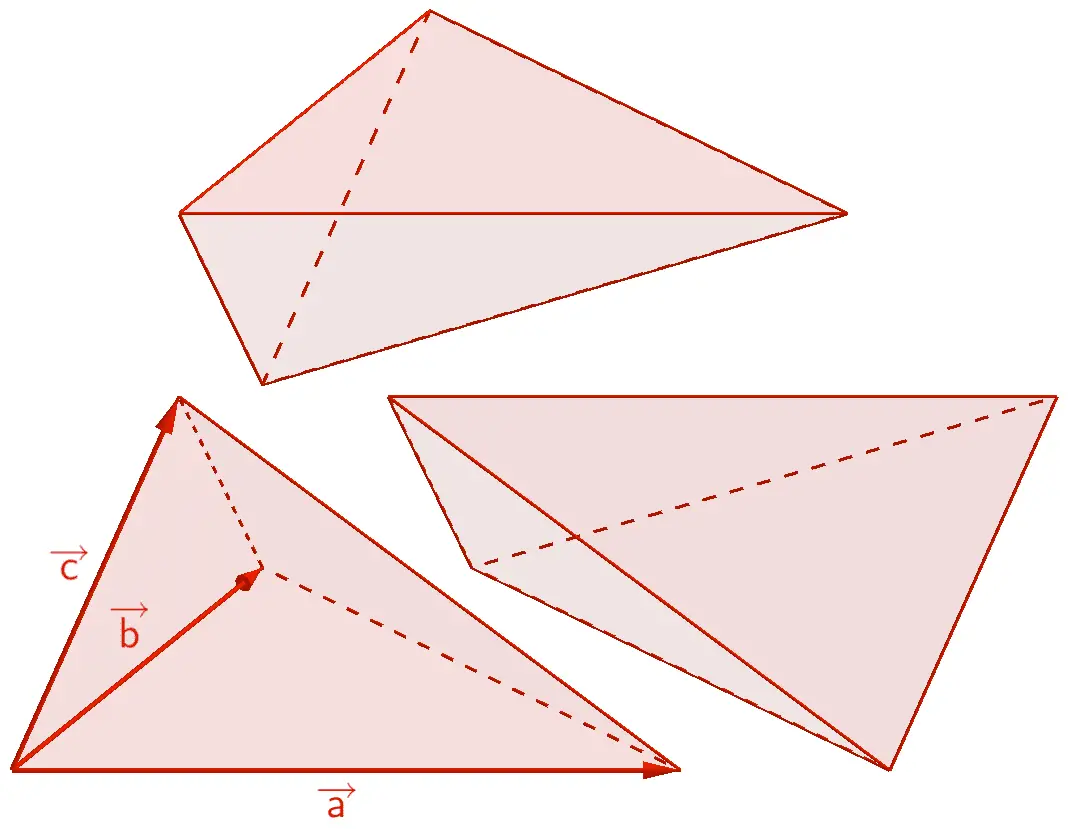
\[\begin{align*} V_{\text{Pyramide}} &= \frac{1}{3} \cdot V_{\text{Prisma}} \\[0.8em] &= \frac{1}{3} \cdot \frac{1}{2} \cdot V_{\text{Spat}} \\[0.8em] &= \frac{1}{6} \cdot \vert \overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c}) \vert \end{align*}\]
Volumen eine dreiseitigen Pyramide (vgl. Merkhilfe)
\[V_{\text{Pyramide}} = \frac{1}{6} \cdot \vert \overrightarrow{a} \circ (\overrightarrow{b} \times \overrightarrow{c}) \vert\]
Beispielaufgabe
Die Punkte \(A(6|1|2)\), \(B(8|8|5)\), \(C(1|6|2)\), \(D(-1|-1|-1)\) und \(S(1{,}5|1{,}5|8)\) legen die gerade Pyramide \(ABCDS\) fest, deren Grundfläche die Raute \(ABCD\) ist.
Berechnen Sie das Volumen \(V\) der Pyramide \(ABCDS\).
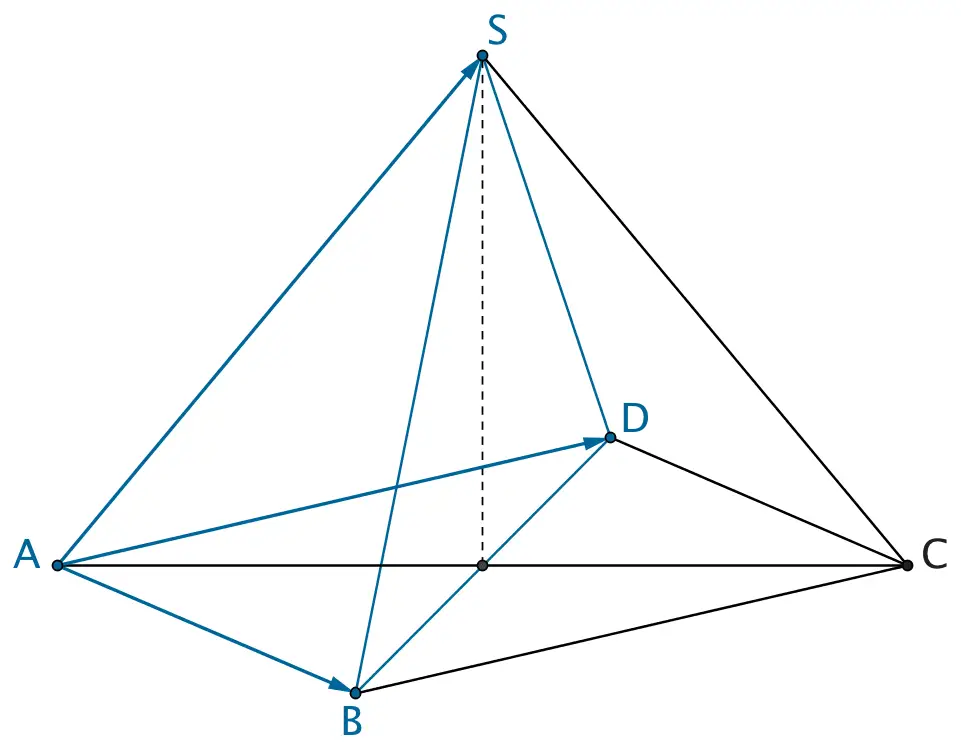
Planskizze: Pyramide \(ABCDS\)
Bei der geraden Pyramide \(ABCDS\) liegt die Spitze \(S\) über dem Schnittpunkt der Diagonalen der Raute \(ABCD\). Das Dreieck \(BDS\) teilt die Pyramide \(ABCDS\) in die beiden volumengleichen dreiseitigen Pyramiden \(ABDS\) und \(BCDS\).
\[\begin{align*}V &= 2 \cdot V_{ABDS} \\[0.8em] &= 2 \cdot \frac{1}{6} \cdot \left| \overrightarrow{AS} \circ \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \overrightarrow{AS} \circ \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \right|\end{align*}\]
Vektoren \(\overrightarrow{AB}\), \(\overrightarrow{AD}\) und \(\overrightarrow{AS}\) berechnen:
\(A(6|1|2)\), \(B(8|8|5)\), \(C(1|6|2)\), \(D(-1|-1|-1)\), \(S(1{,}5|1{,}5|8)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 8 \\ 8 \\ 5 \end{pmatrix} - \begin{pmatrix} 6 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 7 \\ 3 \end{pmatrix}\]
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} -1 \\ -1 \\ -1 \end{pmatrix} - \begin{pmatrix} 6 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -7 \\ -2 \\ -3 \end{pmatrix}\]
\[\overrightarrow{AS} = \overrightarrow{S} - \overrightarrow{A} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 8 \end{pmatrix} - \begin{pmatrix} 6 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -4{,}5 \\ 0{,}5 \\ 6 \end{pmatrix}\]
Volumen der Pyramide \(ABCDS\) berechnen:
\[\begin{align*} V &= \frac{1}{3} \cdot \left| \overrightarrow{AS} \circ \left( \overrightarrow{AB} \times \overrightarrow{AD} \right) \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} -4{,}5 \\ 0{,}5 \\ 6 \end{pmatrix} \circ \left[ \begin{pmatrix} 2 \\ 7 \\ 3 \end{pmatrix} \times \begin{pmatrix} -7 \\ -2 \\ -3 \end{pmatrix} \right] \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} -4{,}5 \\ 0{,}5 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 7 & \cdot & (-3) & - & 3 & \cdot & (-2) \\ 3 & \cdot & (-7) & - & 2 & \cdot & (-3) \\ 2 & \cdot & (-2) & - & 7 & \cdot & (-7) \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \left| \begin{pmatrix} -4{,}5 \\ 0{,}5 \\ 6 \end{pmatrix} \circ \begin{pmatrix} -15 \\ -15 \\ 45 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{3} \cdot \vert (-4{,}5) \cdot (-15) + 0{,}5 \cdot (-15) + 6 \cdot 45 \vert \\[0.8em] &= \frac{1}{3} \cdot 330 \\[0.8em] &= 110 \end{align*}\]
Das Volumen der Pyramide \(ABCDS\) beträgt 110 VE (Volumeneinheiten).


