Im Folgenden werden Schläge betrachtet, bei denen die Flugbahn des Federballs jeweils mithilfe einer Funktion \(h \colon x \mapsto a \cdot \sqrt{b-x} + c\) mit maximalem Definitionsbereich und \(a, b, c \in \mathbb R\) beschrieben wird.
Ermitteln Sie für \(a = 2\), \(b = 5\) und \(c = -2\), in welcher Entfernung zur Netzebene und unter welchem Winkel der Federball auf dem Boden auftrifft.
(4 BE)
Lösung zu Teilaufgabe 3a
\[h(x) = a \cdot \sqrt{b-x} + c, \; a,b,c \in \mathbb R\]
Entfernung zur Netzebene, in der der Federball auftrifft
\(\textcolor{#cc071e}{a = 2}\), \(\textcolor{#0087c1}{b = 5}\), \(\textcolor{#e9b509}{c = -2}\)
\[h_{\textcolor{#cc071e}{2};\textcolor{#0087c1}{5};\textcolor{#e9b509}{-2}}(x) = \textcolor{#cc071e}{2} \cdot \sqrt{\textcolor{#0087c1}{5} - x} \textcolor{#e9b509}{-2}\]
Da die \(x\)-Achse den Boden beschreibt und die Netzebene den Koordinatenursprung enthält (vgl. Angabe), ist für \(x > 0\) die Nullstelle von \(h_{2;5;-2}\) zu berechnen.
\[\begin{align*}h_{2;5;-2}(x) &= 0 \\[0.8em] 2 \cdot \sqrt{5-x}-2 &= 0 &&| + 2\; \text{(Wurzelterm isolieren)} \\[0.8em] 2 \cdot \sqrt{5-x} &= 2 &&| : 2 \\[0.8em] \sqrt{5-x} &= 1 &&| \; (\dots)^2 \; \text{(Gleichung quadrieren)} \\[0.8em] 5 - x &= 1 &&| + x - 1 \\[0.8em] 4 &= x\end{align*}\]
Der Federball trifft in einer Entfernung von 4 m zur Netzebene auf dem Boden auf.
Winkel, unter dem der Federball auf dem Boden auftrifft
 ergänzende Darstellung
ergänzende Darstellung
Der Winkel, unter dem der Federball auf dem Boden auftrifft, entspricht im Modell dem Schnittwinkel, den der Graph der Funktion \(h_{2;5;-2}\) im Punkt \((4|0)\) mit der \(x\)-Achse einschließt.
Tangentensteigung und Normalensteigung
\[\textcolor{#cc071e}{m_{T}} = f'(x_0) \qquad \textcolor{#0087c1}{m_{N}} = -\dfrac{1}{f'(x_0)}\]
Steigungswinkel \(\boldsymbol{\alpha}\) einer Tangente
\[{\textcolor{#cc071e}{\tan{\alpha}}} = f'(x_0)\]
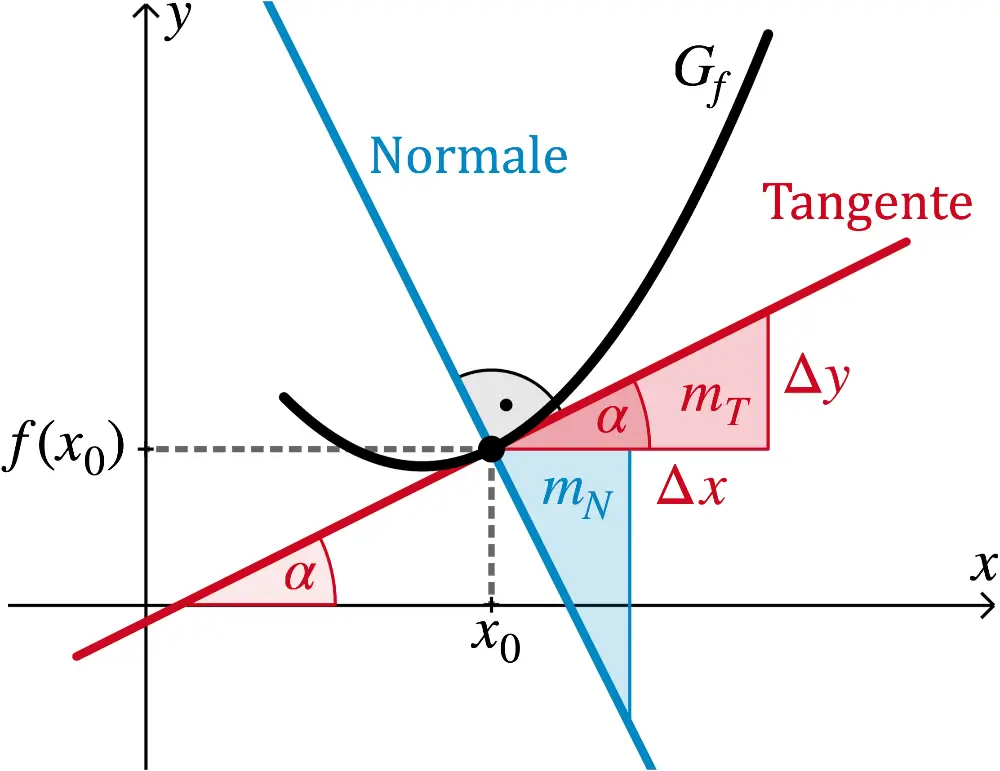
Für den Steigungswinkel \(\textcolor{#cc071e}{\alpha}\), der Tangente an den Graphen von \(h_{2;5;-2}\) an der Stelle \(x = 4\) gilt:
\[\textcolor{#cc071e}{\tan{\alpha}} = h'_{2;5;-2}(4)\]
Erste Ableitung \(h'_{2;5;-2}\) bestimmen:
Hierfür wird u. a. die Kettenregel benötigt. Es kann hilfreich sein, den Wurzelterm in der Potenzschreibweise zu formulieren.
\[\begin{align*}h_{2;5;-2}(x) &= 2 \cdot \sqrt{5-x} -2 &&| \; \sqrt{a} = a^{\frac{1}{2}} \\[0.8em] &= 2 \cdot (5-x)^{\frac{1}{2}} - 2\end{align*}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Ohne Potenzschreibweise:
\[h_{2;5;-2}(x) = 2 \cdot \sqrt{5-x} - 2\]
\[\begin{align*}h'_{2;5;-2}(x) &= 2 \cdot \frac{1}{2\sqrt{5-x}} \cdot (-1)\\[0.8em] &= -\frac{1}{\sqrt{5-x}}\end{align*}\]
Mit Potenzschreibweise:
\[h_{2;5;-2}(x) = 2 \cdot (5-x)^{\frac{1}{2}} - 2\]
\[\begin{align*}h'_{2;5;-2}(x) &= 2 \cdot \frac{1}{2} \cdot (5-x)^{-\frac{1}{2}} \cdot (-1)\\[0.8em] &= -(5-x)^{\frac{1}{2}} &&|\; a^{\frac{1}{2}} = \sqrt{x}, \; a^{-r} = \frac{1}{a^r} \\[0.8em] &= -\frac{1}{\sqrt{5-x}}\end{align*}\]
Steigungswinkel \(\textcolor{#cc071e}{\alpha}\) berechnen:
 ergänzende Darstellung
ergänzende Darstellung
Der Steigungswinkel einer Gerade ist der im mathematisch positiven Sinn (gegen den Uhrzeigersinn) gemessene Winkel \(\textcolor{#cc071e}{\alpha}\), den die Gerade (hier Tangente) mit der positiven \(x\)-Achse einschließt.
Im vorliegenden Fall einer negativen Tangentensteigung gibt der Taschenrechner den Steigungswinkel \(\textcolor{#cc071e}{\alpha'}\), den die Tangente mit der negativen \(x\)-Achse einschließt, im mathematisch negativen Sinn (im Uhrzeigersinn) aus. Der Schnittwinkel ist dann betragsmäßig gleich groß, aber positiv.
\[\textcolor{#cc071e}{\tan{\alpha}} = h'_{2;5;-2}(4) = -\frac{1}{\sqrt{5-4}} = -1 \quad|\; \text{TR:} \; \tan^{-1}(\dots)\]
\(\Rightarrow \textcolor{#cc071e}{\alpha'} = \tan^{-1}(-1) = \textcolor{#cc071e}{-45^{\circ}}\)
\(\Rightarrow\) Schnittwinkel 45°
Der Federball trifft in einer Entfernung von 4 m zur Netzebene unter einem Winkel von 45° auf dem Boden auf.


