Die tiefste Stelle eines Schiffs bewegt sich im Modell auf der Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 0\\-17\\-8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0\\1\\0 \end{pmatrix}, \, \lambda \in \mathbb R\). Beurteilen Sie anhand einer Rechnung, ob das Schiff das Sperrwerk passieren kann, wenn das Sperrtor geöffnet ist.
(5 BE)
Lösung zu Teilaufgabe f
\[g \colon \overrightarrow{X} = \begin{pmatrix} 0\\-17\\\textcolor{#e9b509}{-8} \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0\\1\\0 \end{pmatrix}, \, \lambda \in \mathbb R\]
Der \(x_3\)-Koordinate des Stützvektors der Geradengleichung von \(g\) ist zu entnehmen, dass sich die tiefste Stelle des Schiffs 8 m unterhalb der Wasseroberfläche bewegt.
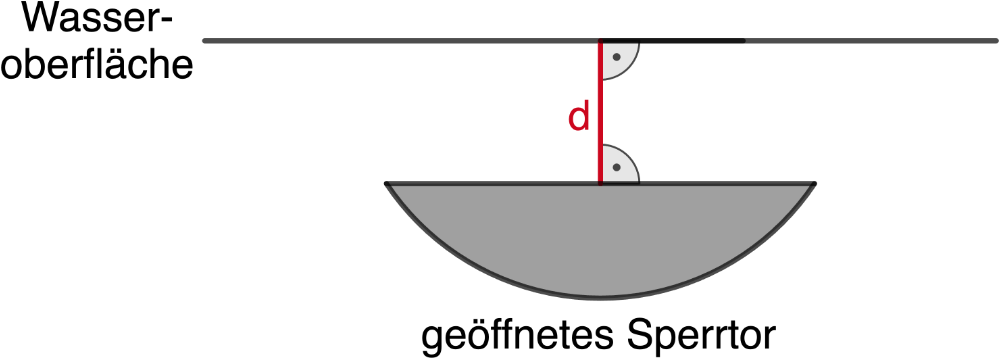Abb. 2a, ergänzende Eintragung
Die rechteckige Seitenfläche des geöffneten Sperrtors ist parallel zur Wasseroberfläche und hat zu dieser den Abstand \(\textcolor{#cc071e}{d}\). Um beurteilen zu können, ob das Schiff das Sperrwerk bei geöffnetem Sperrtor passieren kann, muss dieser Abstand berechnet werden.
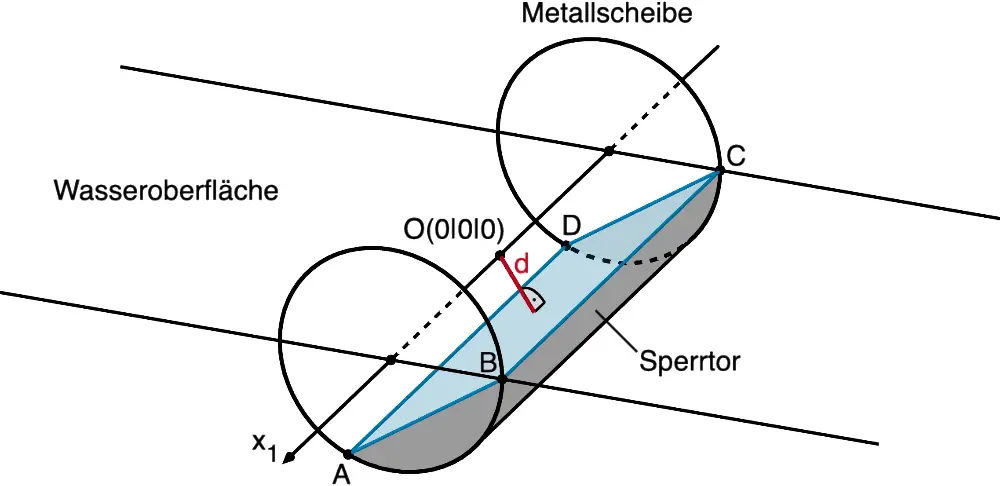Abb. 1, ergänzende Eintragung
In der in Abbildung 1 gezeigten Position liegt die rechteckige Seitenfläche des Sperrtors (Rechteck \(ABCD\)) in der Ebene \(\textcolor{#0087c1}{E}\) (vgl. Angabe und Teilaufgabe b). Da sich das Sperrtor während eines Schließvorgangs um die \(x_1\)-Achse dreht, ist der Abstand des Koordinatenursprungs von der Ebene \(\textcolor{#0087c1}{E}\) gleich dem Abstand \(\textcolor{#cc071e}{d}\) der rechteckigen Seitenfläche des geöffneten Sperrtors von der Wasseroberfläche.
Abstand \(\textcolor{#cc071e}{d} = d(O;\textcolor{#0087c1}{E})\) berechnen:
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
1. Mit der Hesseschen Normalenform (HNF)
Hessesche Normalenform von \(\textcolor{#0087c1}{E}\) aufstellen:
\[\begin{align*} &\textcolor{#0087c1}{E}\colon 2x_2-3x_3-26 = 0 &&| : \vert \overrightarrow{n} \vert = \left| \begin{pmatrix} 0\\2\\-3 \end{pmatrix} \right| \\[0.8em] &\textcolor{#0087c1}{E}\colon \frac{2x_2-3x_3-26}{\sqrt{0^2+2^2+(-3)^2}} = 0 \\[0.8em] &\textcolor{#0087c1}{E}\colon \frac{2x_2-3x_3-26}{\sqrt{13}} = 0 &&\text{(HNF)} \end{align*}\]
Abstand \(\textcolor{#cc071e}{d} = d(O;\textcolor{#0087c1}{E})\) berechnen:
\[\textcolor{#0087c1}{E}\colon \frac{2x_2-3x_3-26}{\sqrt{13}} = 0 \quad\text{(HNF)}\]
Koordinatenursprung \(O(0|0|0)\)
\[\textcolor{#cc071e}{d} = d(O;\textcolor{#0087c1}{E}) =\left| \frac{2 \cdot 0 - 3 \cdot 0 -26}{\sqrt{13}} \right| = \textcolor{#cc071e}{2\sqrt{13}} \approx \textcolor{#cc071e}{7{,}2}\]
Die rechteckige Seitenfläche des geöffneten Sperrtors liegt etwa 7,2 m unterhalb der Wasseroberfläche. Da sich die tiefste Stelle des Schiffs 8 m unterhalb der Wasseroberfläche befindet, kann das Schiff das Sperrwerk nicht passieren.
2. Mit dem Lotfußpunktverfahren
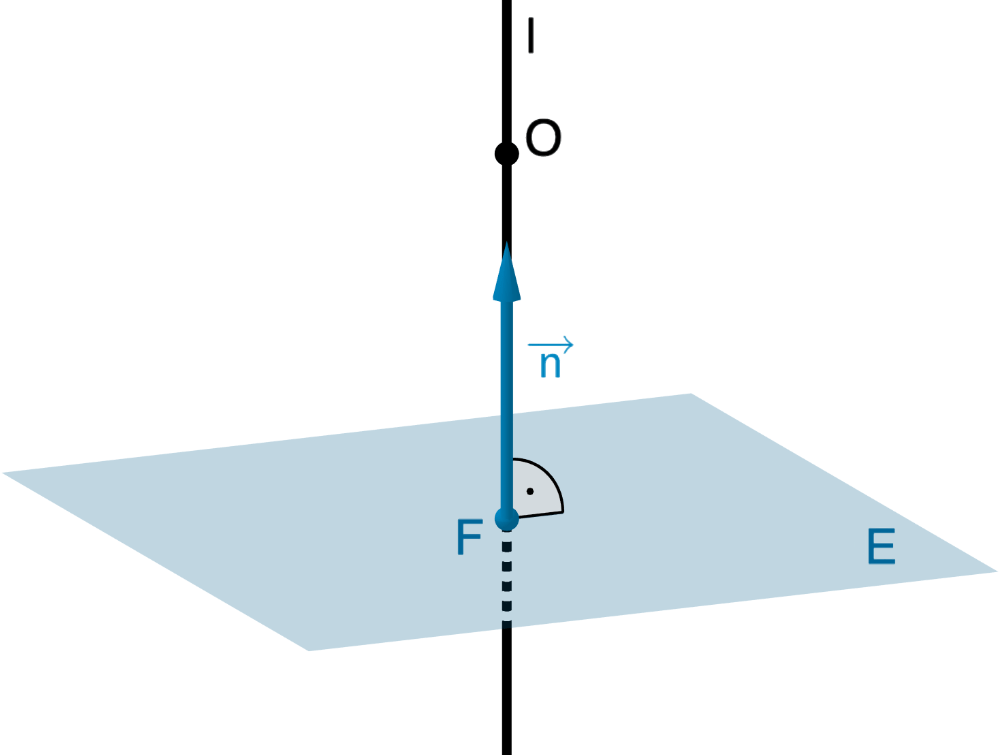schematische Darstellung
Die Lotgerade \(l\) durch den Koordinatenursprung \(O\) auf die Ebene \(\textcolor{#0087c1}{E}\) schneidet die Ebene \(\textcolor{#0087c1}{E}\) im Lotfußpunkt \(\textcolor{#0087c1}{F}\).
\[d(O;\textcolor{#0087c1}{E}) = \vert \overrightarrow{O\textcolor{#0087c1}{F}} \vert = \vert \textcolor{#0087c1}{\overrightarrow{F}} \vert\]
\[\textcolor{#0087c1}{E}\colon 2x_2-3x_3-26 = 0\]
Gleichung der Lotgeraden \(l\) durch \(O(0|0|0)\) auf \(\textcolor{#0087c1}{E}\):
\[l \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0\\2\\-3 \end{pmatrix} = \lambda \cdot \begin{pmatrix} 0\\2\\-3 \end{pmatrix},\; \lambda \in \mathbb R\]
Lotfußpunkt \(\textcolor{#0087c1}{F}\) bestimmen:
Der Lotfußpunkt \(\textcolor{#0087c1}{F}\) ist der Schnittpunkt der Lotgeraden \(l\) und der Ebene \(\textcolor{#0087c1}{E}\).
\[\begin{align*}l \cap \textcolor{#0087c1}{E} \colon 2 \cdot 2\lambda - 3 \cdot (-3\lambda) -26 &=0 \\[0.8em] 13\lambda -26 &=0 &&| + 26 \\[0.8em] 13\lambda &= 26 &&| : 13 \\[0.8em] \lambda &= 2 \end{align*}\]
\(\lambda = 2\) in die Gleichung der Lotgeraden \(l\) eingesetzt, ergibt den Ortsvektor des Lotfußpunktes \(\textcolor{#0087c1}{F}\).
\[\textcolor{#0087c1}{F} \in l \colon \textcolor{#0087c1}{\overrightarrow{F}} = 2 \cdot \begin{pmatrix} 0\\2\\-3 \end{pmatrix} = \textcolor{#0087c1}{\begin{pmatrix} 0\\4\\-6 \end{pmatrix}}\]
Abstand \(\textcolor{#cc071e}{d} = d(O;\textcolor{#0087c1}{E})\) berechnen:
\[\begin{align*}\textcolor{#cc071e}{d} &= d(O;\textcolor{#0087c1}{E}) = \vert \overrightarrow{O\textcolor{#0087c1}{F}} \vert = \vert \textcolor{#0087c1}{\overrightarrow{F}} \vert = \left| \textcolor{#0087c1}{\begin{pmatrix} 0\\4\\-6 \end{pmatrix}} \right| \\[0.8em] &= \sqrt{0^2 + 4^2 + (-6)^2} = \textcolor{#cc071e}{2\sqrt{13}} \approx \textcolor{#cc071e}{7{,}2}\end{align*}\]
Die rechteckige Seitenfläche des geöffneten Sperrtors liegt etwa 7,2 m unterhalb der Wasseroberfläche. Da sich die tiefste Stelle des Schiffs 8 m unterhalb der Wasseroberfläche befindet, kann das Schiff das Sperrwerk nicht passieren.
3. Elementargeometrisch, Trigonometrie im rechtwinkligen Dreieck
Unter Berücksichtigung der Ergebnisse aus den Teilaufgaben c und d geht es auch einfacher
Abb. 1, ergänzende Eintragung
In Abbildung 1 entspricht der gesuchte Abstand \(\textcolor{#cc071e}{d}\) der Senkrechten vom Mittelpunkt der vorderen Metallscheibe auf die Seite \([AB]\) des Rechtecks \(ABCD\). Der Mittelpunkt der Metallscheibe und der Mittelpunkt der Seite \([AB]\) bilden mit Punkt \(B\) ein rechtwinkliges Dreieck. (vgl. Abbildung).
Die Größe des Winkels \(\varphi\) ist aus Teilaufgabe c bekannt: \(\varphi \approx 33{,}7^{\circ}\).
Der Radius \(r\) der Metallscheibe entspricht im Modell der \(x_2\)-Koordinate des Punktes \(B(30|13|0)\) (vgl. Teilaufgabe d).
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
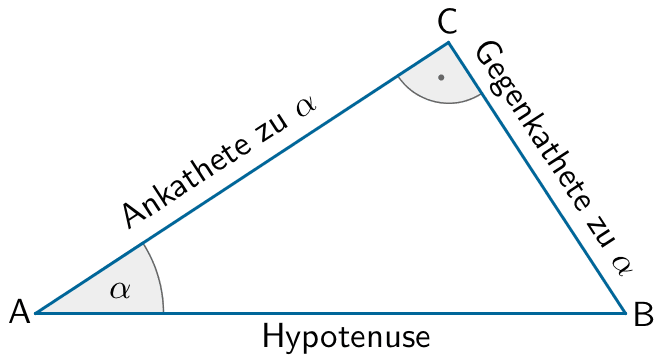
Es gilt:
\[\begin{align*}\sin{\varphi} = \dfrac{\textcolor{#cc071e}{d}}{r} \; \Leftrightarrow \; \textcolor{#cc071e}{d} &= r \cdot \sin{\varphi}\\[0.8em] &= 13 \cdot \sin{33{,}7^{\circ}} \\[0.8em] &\approx \textcolor{#cc071e}{7{,}2}\end{align*} \]
Die rechteckige Seitenfläche des geöffneten Sperrtors liegt etwa 7,2 m unterhalb der Wasseroberfläche. Da sich die tiefste Stelle des Schiffs 8 m unterhalb der Wasseroberfläche befindet, kann das Schiff das Sperrwerk nicht passieren.
