Im Folgenden wird ein Sperrwerk an einem Fluss betrachtet, das dem Schutz vor Überflutungen bei Sturmfluten dient. Ein Teil dieses Sperrwerks besteht aus zwei kreisförmigen Metallscheiben, an denen ein Sperrtor befestigt ist. Durch Drehung der Metallscheiben wird das Sperrtor in verschiedene Stellungen gebracht.
In einem Koordinatensystem werden die beiden Metallscheiben durch die Grund- und die Deckfläche eines geraden Zylinders dargestellt. Die \(x_1\)-Achse verläuft durch die Mittelpunkte dieser beiden Kreisflächen und entspricht der Drehachse der Metallscheiben.
Die Ebene \(E\) schneidet den Zylinder im Rechteck \(ABCD\) und zerlegt diesen in zwei Teilkörper. Der kleinere Teilkörper entspricht dem Sperrtor in einer speziellen Stellung (vgl. Abbildung 1). Eine Längeneinheit entspricht einem Meter in der Realität.
Es wird vereinfachend ausschließlich ein Wasserstand betrachtet, bei dem die Wasseroberfläche im Modell in der \(x_1x_2\)-Ebene liegt.

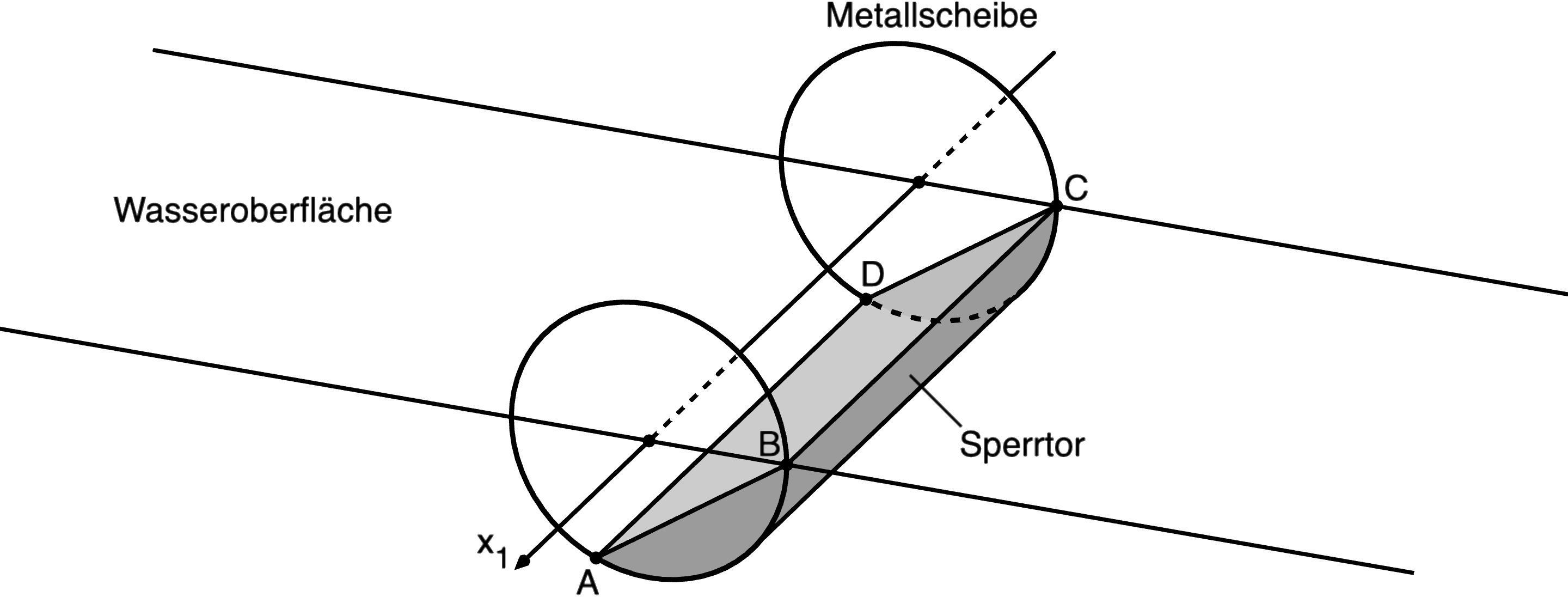Abb. 1

Geben Sie den Durchmesser einer Metallscheibe und den Abstand der beiden Metallscheiben jeweils in Metern an.

(2 BE)

Lösung zu Teilaufgabe d

Durchmesser einer Metallscheibe: 26 m

Abstand der Metallscheiben: 60 m

Ergänzende Erklärung (nicht verlangt)

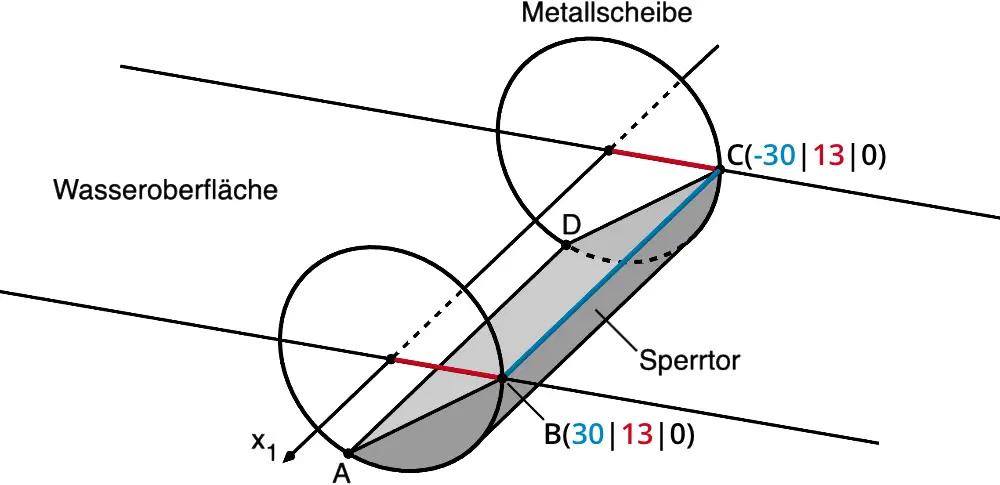
Die \(\textcolor{#cc071e}{x_2}\)-Koordinate der Punkte \(B\) und \(C\) beschreibt im Modell den Radius einer Metallscheibe. Eine Längeneinheit entspricht einem Meter (vgl. Angabe)

Durchmesser einer Metallscheibe: \(2 \cdot \textcolor{#cc071e}{13\,\textsf{m}} = 26\,\textsf{m}\)

Der Abstand der Metallscheiben ergibt sich aus der Differenz der \(\textcolor{#0087c1}{x_1}\)-Koordinaten der Punkte \(B\) und \(C\).

Abstand der Metallscheiben: \((\textcolor{#0087c1}{30} - (\textcolor{#0087c1}{-30}))\,\textsf{m} = 60\,\textsf{m}\)