Zeichnen Sie die Pyramide \(EFGHS_{15}\) in Abbildung 1 ein. Die Seitenfläche \(EFS_{15}\) und die Grundfläche \(EFGH\) dieser Pyramide schließen einen Winkel ein. Begründen Sie ohne weitere Rechnung, dass die Größe dieses Winkels kleiner als 45° ist; verwenden Sie dazu folgende Information:
Für den Mittelpunkt \(M\) des Quadrats \(EFGH\) und den Punkt \(N\) mit \( \overrightarrow{N} = \dfrac{1}{2} \cdot (\overrightarrow{E} + \overrightarrow{F})\) gilt \(\overline{MS_{15}} < \overline{MN}\).
(4 BE)
Lösung zu Teilaufgabe d
Einzeichnen der Pyramide \(EFGHS_{15}\)
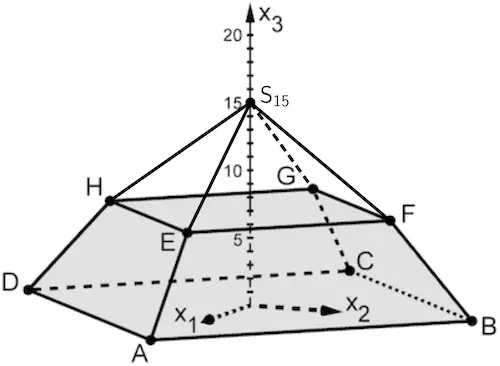 Abb. 1
Abb. 1
Für \(k = 15\) und \(S_k(0|0|k)\) (vgl. Teilaufgabe c) ist \(S_{15}(0|0|15)\) die Spitze der Pyramide \(EFGHS_{15}\).
Begründung, dass der Winkel den die Seitenfläche \(EFS_{15}\) und die Grundfläche \(EFGH\) einschließen, kleiner als 45° ist
\(N\) ist der Mittelpunkt der Strecke \([EF]\). Das Dreieck \(S_{15}NM\) ist bei \(M\) rechtwinklig. Die Größe des Winkels bei \(N\) entspricht der Größe des betrachteten Winkels. Wegen \(\overline{MS_{15}} < \overline{MN}\) ist der Winkel bei \(N\) kleiner als 45°.
Ausführliche Erklärung (nicht verlangt)
![Mittelpunkt N der Strecke [EF], Mittelpunkt M des Quadrats EFGH, Spitze S₁₅ der Pyramide EFGHS₁₅, Stützdreieck S₁₅NM der Seitenfläche EFS₁₅](/images/stories/B2023_PT_B_G1/B2023_PT_B_G1_d2.png) Abb. 1
Abb. 1
Planskizze (optional): Wegen \( \overrightarrow{N} = \dfrac{1}{2} \cdot (\overrightarrow{E} + \overrightarrow{F})\) ist der Punkt \(N\) Mittelpunkt der Strecke \(EF\).
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
Das Dreieck \(\textcolor{#0087c1}{S_{15}NM}\) ist bei \(M\) rechtwinklig. Es ist Stützdreieck der Seitenfläche \(\textcolor{#0087c1}{EFS_{15}}\) gegen die Grundfläche \(EFGH\) der Pyramide \(EFGHS_{15}\). Die Größe des Winkels bei \(N\) entspricht der Größe des Winkels, den die Seitenfläche \(\textcolor{#0087c1}{EFS_{15}}\) und die Grundfläche \(EFGH\) einschließen.
![Rechtwinkliges Dreieck S₁₅NM im Vergleich zu einem gleichschenklig rechtwinkligen Dreieck mit der Seite [MN]](/images/stories/B2023_PT_B_G1/B2023_PT_B_G1_d3.png)
Planskizze (empfohlen): Da das Dreieck \(\textcolor{#0087c1}{S_{15}MN}\) nicht gleichschenklig rechtwinklig ist, sondern \(\textcolor{#0087c1}{\overline{MS_{15}} < \overline{MN}}\) gilt, ist die Größe des Winkels bei \(\textcolor{#0087c1}{N}\) und somit die Größe des Winkels, den die Seitenfläche \(EFS_{15}\) und die Grundfläche \(EFGH\) einschließen, kleiner als 45°.


