Berechnen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau.
(5 BE)
Lösung zu Teilaufgabe 2b
Steigungswinkel einer Tangente, Anwenden einer Funktion im Sachzusammenhang
Größe des Winkel, den das Seil mit Mast 2 im Aufhängepunkt einschließt
\[f(x) = e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}; \; D = \mathbb R\]
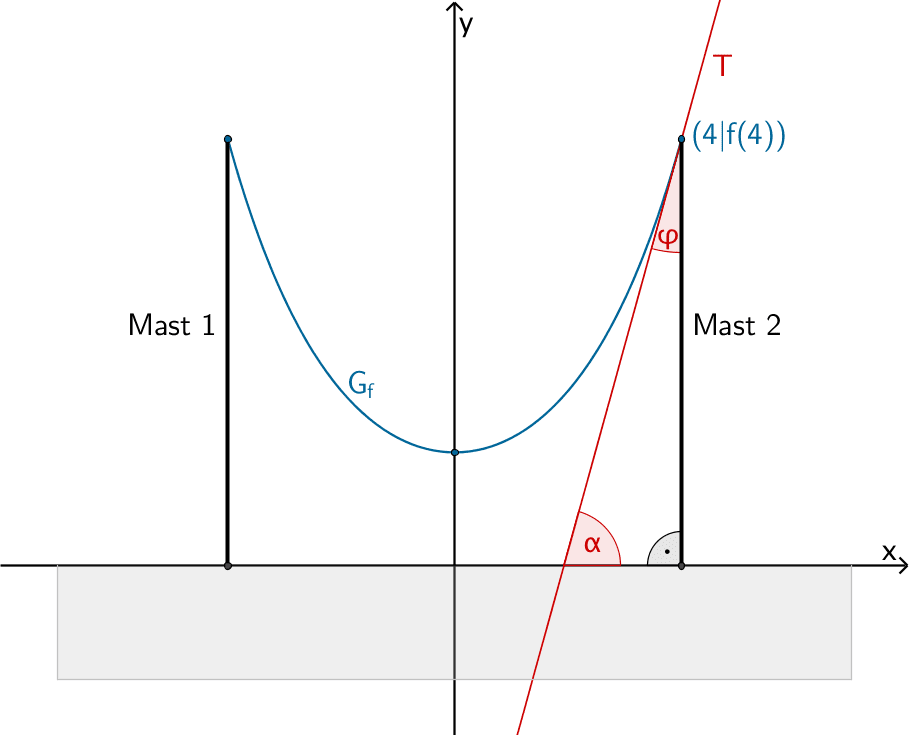
Der Winkel, den das Seil mit Mast 2 im Aufhängepunkt einschließt, entspricht dem spitzen Winkel \(\varphi\), den die Tangente \(T\) an den Graphen der Funktion \(f\) im Aufhängepunkt \((4|f(4))\) und das Lot des Aufhängepunkts auf die \(x\)-Achse (Mast 2) einschließt. Der Winkel \(\varphi\) lässt sich berechnen, indem man zunächst den Steigungswinkel \(\alpha\) der Tangente \(T\) bestimmt und anschließend den Ergänzungswinkel zu 90° (Komplementwinkel) berechnet.
\[\varphi = 90^{\circ} - \alpha\]
Steigungswinkel \(\alpha\) der Tangente \(T\) berechnen:
Für die Steigung \(m_{T}\) der Tangente \(T\) an \(G_{f}\) im Punkt \((4|f(4))\) gilt:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = f'(4)\]
Für den Steigungswinkel \(\alpha\) der Tangente \(T\) gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan \alpha = m_{T}\]
\[\Longrightarrow \quad \tan \alpha = f'(4)\]
Aus Teilaufgabe 1c ist bekannt:
\[f'(x) = \frac{1}{2} \cdot \left( e^{\frac{1}{2}x} - e^{-\frac{1}{2}x} \right)\]
Steigungswinkel \(\alpha\) der Tangente \(T\) berechnen:
\[\begin{align*} \tan \alpha &= f'(4) \\[0.8em] &= \frac{1}{2} \cdot \left( e^{\frac{1}{2} \cdot \, 4} - e^{-\frac{1}{2} \cdot \, 4} \right) \\[0.8em] &= \frac{1}{2} \cdot \left( e^{2} - e^{-2} \right) & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[2.4em] \alpha &\approx 74{,}59^{\circ} \end{align*}\]
Winkel \(\varphi\) berechnen:
\[\begin{align*}\varphi &= 90^{\circ} - \alpha \\[0.8em] &= 90^{\circ} - 74{,}59^{\circ} \\[0.8em] &= 15{,}41^{\circ}\end{align*}\]
Auf der Grundlage des Modells, beträgt die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, ca. 15,41°.
Länge des zwischen den Masten hängenden Seils
Die Länge des zwischen den Masten hängenden Seils entspricht der Kurvenlänge \(L_{-4;4}\) des Funktionsgraphen von \(f\) zwischen den Punkten \((-4|f(-4))\) und \((4|f(4))\) in Metern (vgl. Angabe zu Teilaufgabe 1h).
Kurvenlänge aus Teilaufgabe 1h:
\[L_{0;b} = e^{\frac{1}{2}b} - e^{-\frac{1}{2}b}\]
Wegen der Achsensymmetrie von \(G_{f}\) (vgl. Teilaufgabe 1b) gilt: \(L_{-4;4} = 2 \cdot L_{0;4}\).
\[\begin{align*} L_{-4;4} &= 2 \cdot L_{0;4} \\[0.8em] &= 2 \cdot \left( e^{\frac{1}{2} \cdot \, 4} - e^{-\frac{1}{2} \cdot \, 4} \right) \\[0.8em] &= 2 \cdot \left( e^{-2} - e^{-2} \right) \\[0.8em] &\approx 14{,}51 \end{align*}\]
Die Länge des zwischen den Masten hängenden Seils beträgt ca. 14,51 m.


