Das Newton-Verfahren geht von einem geeigneten Startwert \(x_{0}\) für eine gesuchte Nullstelle \(x_{N}\) aus und errechnet durch wiederholtes Anwenden der Newton'schen Iterationsformel (Rechenvorschrift) weitere (genauere) Näherungswerte der Nullstelle.
Newton'sche Iterationsformel (vgl. Merkhilfe)
\[x_{n + 1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}\,; \enspace n \in \mathbb N\]
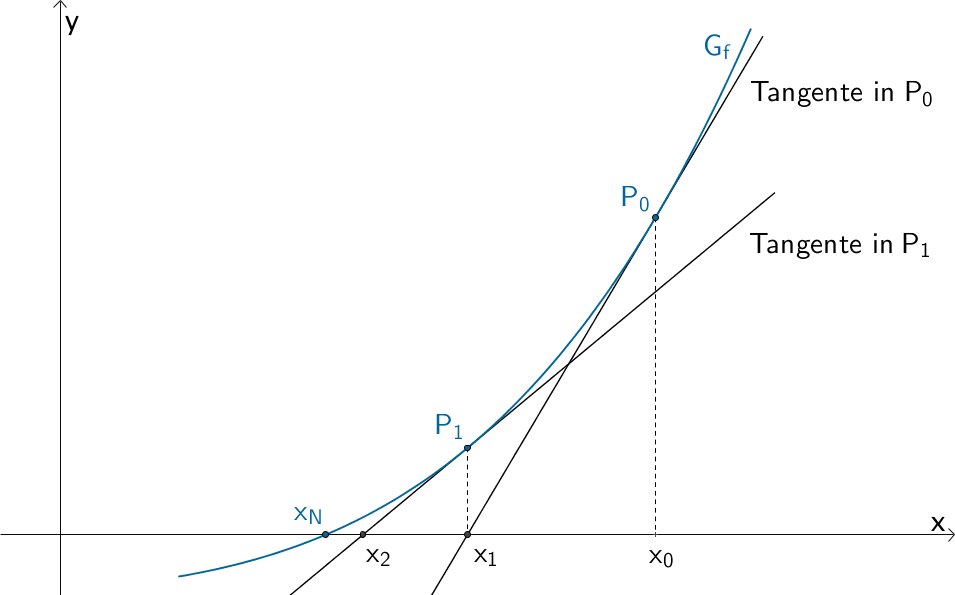
Newton-Verfahren: Ist \(x_{0}\) ein Startwert in der Umgebung der Nullstelle \(x_{N}\), so nähert die Tangente in \(P_{0}\) den Graphen \(G_{f}\) in der Umgebung der Nullstelle an. Die Tangente schneidet die \(x\)-Achse an der Stelle \(x_1\), die bei geeignetem Startwert \(x_{0}\) eine bessere Näherung für die gesuchte Nullstelle \(x_{N}\) darstellt als der Startwert \(x_{0}\). Wiederholt man dieses Verfahren, erhält man (unter bestimmten Voraussetzungen) eine Folge \(x_{0}, x_{1}, x_{2} ...\) von immer besseren Näherungswerten.
Der Näherungswert \(x_{1}\) lässt sich berechnen, indem man die Steigung \(m_{T}\) der Tangente durch die Punkte \(P_{0}(x_{0}|f(x_{0}))\) und \((x_{1}|0)\) formuliert (vgl. Abiturskript - 1.1.1 Lineare Funktion, Steigung \(m\)), diese mit \(m_{T} = f'(x_{0})\) ersetzt (vgl. Abiturskript - 1.5.1 Die Ableitung, Tangentensteigung) und die Gleichung nach \(x_{1}\) auflöst.
\[\begin{align*} \frac{f(x_{0}) - 0}{x_{0} - x_{1}} &= m_{T} & &| \; m_{T} = f'(x_{0}) \\[0.8em] \frac{f(x_{0})}{x_{0} - x_{1}} &= f'(x_{0}) & &| \cdot (x_{0} - x_{1}) \\[0.8em] f(x_{0}) &= f'(x_{0}) \cdot (x_{0} - x_{1}) & &| : f'(x_{0}) \\[0.8em] \frac{f(x_{0})}{f'(x_{0})} &= x_{0} - x_{1} & &| + x_{1} - \frac{f(x_{0})}{f'(x_{0})} \\[0.8em] x_{1} &= x_{0} - \frac{f(x_{0})}{f'(x_{0})} \end{align*}\]
Analog lassen sich weitere Näherungswerte errechnen (vgl. Newton'sche Iterationsformel).
Wahl eines geeigneten Startwerts \(x_{0}\)
Soll eine Gleichung der Form \(f(x) = 0\) näherungsweise mit dem Newton-Verfahren gelöst werden, lässt sich häufig ein geeigneter Startwert \(x_{0}\) ermitteln, indem man den Graphen der zugehörigen Funktion skizziert. Bei komplizierten Gleichungen kann man versuchen, die Gleichung durch Termumformung in zwei einfachere Funktionen aufzuspalten.
\[f(x) = 0 \quad \Longleftrightarrow \quad f_{1}(x) = f_{2}(x)\]
Anschließend skizziert man die Graphen der Funktionen \(f_{1}\) und \(f_{2}\) und entnimmt in der Nähe des Schnittpunkts der Graphen einen geeigneten Startwert \(x_{0}\).
Die Tangente an den Graphen einer Funktion an der Stelle des Startwerts \(x_{0}\) sollte den Graphen möglichst gut annähern. Dies ist dann der Fall, wenn der Graph an der Stelle des Startwerts \(x_{0}\) einen ähnlichen Verlauf zeigt wie an der gesuchten Nullstelle \(x_{N}\).
Ungeeignet sind Startwerte in deren Umgebung die Tangente an den Graphen einer Funktion nahezu parallel zur \(x\)-Achse verläuft, beispielsweise in der Nähe eines relativen Extremwerts oder eines Terrassenpunkts. Der Schnittpunkt der Tangente mit der \(x\)-Achse liegt dann meist in großer Entfernung zum Startwert \(x_{0}\).
Unmöglich als Startwert \(x_{0}\) sind alle Stellen in denen der Graph einer Funktion eine waagrechte Tangente besitzt (Relative Extrempunkte, Terrassenpunkte), da dann kein Schnittpunkt der Tangente mit der \(x\)-Achse und somit auch kein Näherungswert existiert. Dies ergibt sich auch unmittelbar aus der Newton'sche Iterationsformel \(x_{n + 1} = x_{n} - \dfrac{f(x_{n})}{f'(x_{n})}\), denn es gilt \(f'(x_{n}) \neq 0\).
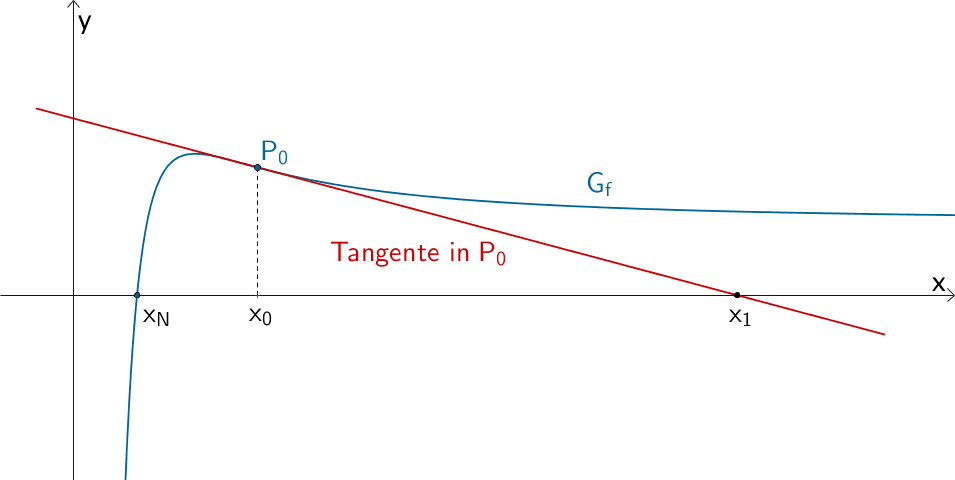
Ungeeigneter Startwert \(x_{0}\) in der Nähe einer Extremstelle
Beispielaufgabe
Gegeben seien die in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto x^{2} + 2\) und \(g \colon x \mapsto e^{x}\) sowie die Funktion \(h \colon x \mapsto f(x) - g(x)\).
Skizzieren Sie die Graphen der Funktionen \(f\) und \(g\) in ein gemeinsames Koordinatensystem. Lösen Sie anschließend die Gleichung \(h(x) = 0\) näherungsweise, idem Sie den ersten Schritt des Newton-Verfahrens mit einem geeigneten Startwert \(x_{0}\) durchführen.
\[f(x) = x^{2} + 2; \; D_{f} = \mathbb R\]
\[g(x) = e^{x}; \; D_{g} = \mathbb R\]
\[h(x) = f(x) - g(x) = x^{2} + 2 - e^{x}; \; D_{h} = \mathbb R\]
Skizzieren der Graphen der Funktionen \(f\) und \(g\)
Mithilfe einer Wertetabelle oder anhand charakteristischer Funktionswerte skizziert man die Graphen der Funktionen \(f\) und \(g\).
Der Graph der Funktion \(f\) ist eine um 2 in \(y\)-Richtung verschobene Normalparabel mit dem Scheitelpunkt \(S(0|2)\) (vgl. Abiturskript - 1.1.2 Quadratische Funktion und Abiturskript - 1.1.7 Entwicklung von Funktionen).
Der Graph der Natürlichen Exponentialfunktion \(g\) verläuft durch die Punkte \((0|1)\) und \((1|e)\). Er nähert sich für \(x \to -\infty\) asymptotisch der \(x\)-Achse an (vgl. Abiturskript - 1.3.1 Natürliche Exponetial- und Logarithmusfunktion, Eigenschaften und Rechenregeln).
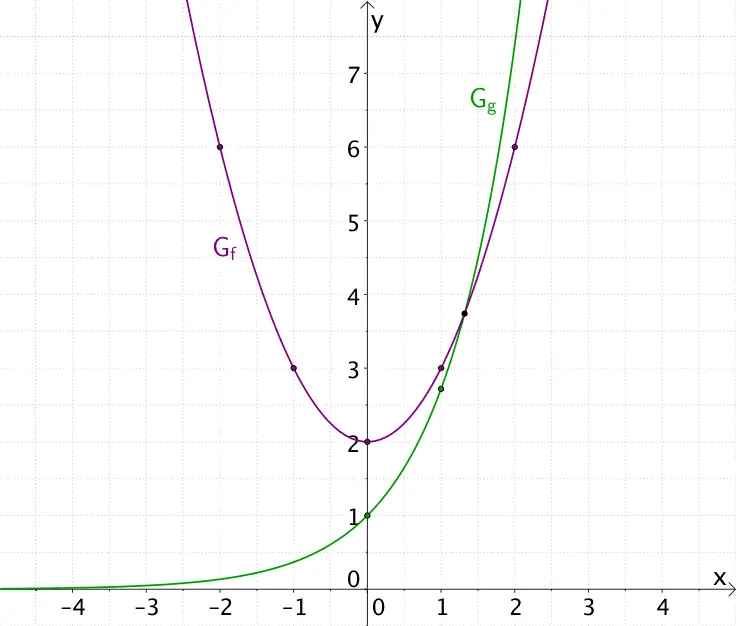
Der Graph der Natürlichen Exponentialfunktion \(g\) geht für \(x \to +\infty\) schneller gegen Unendlich als der Graph der quadratischen Funktion \(f\). Die Graphen schneiden sich im Intervall \([1;2]\).
Lösen der Gleichung \(h(x) = 0\) mithilfe des Newton-Verfahrens
\[\begin{align*}h(x) &= 0 \\[0.8em] f(x) - g(x) &= 0 \\[0.8em] f(x) &= g(x)\end{align*}\]
Die Lösung der Gleichung \(h(x) = 0\) entspricht der Bestimmung der Schnittstelle der Graphen der Funktionen \(f\) und \(g\). Aus der Skizze der Graphen \(G_{f}\) und \(G_{g}\) liest man \(x_{0} = 1\) als geeigneten Startwert für den ersten Schritt des Newton-Verfahrens ab und löst damit näherungsweise die Gleichung \(h(x) = 0\).
\[x_{1} = x_{0} - \frac{h(x_{0})}{h'(x_{0})}\,; \quad x_{0} = 1\]
Erste Ableitung \(h'\) bilden:
\[h(x) = x^{2} + 2 - e^{x}\]
Die Erste Ableitung \(h'\) kann mithilfe der Summenregel, der Potenzregel und der Ableitung der Natürlichen Exponentialfunktion gebildet werden (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[h'(x) = 2 \cdot x^{1} + 0 - e^{x} = 2x - e^{x}\]
Näherungswert \(x_{1}\) berechnen:
\[h(x) = x^{2} + 2 - e^{x}\]
\[h'(x) = 2x - e^{x}\]
\[x_{0} = 1\]
\[\begin{align*}x_{1} &= x_{0} - \frac{h(x_{0})}{h'(x_{0})} \\[0.8em] &= 1 - \frac{h(1)}{h'(1)} \\[0.8em] &= 1 - \frac{1^{2} + 2 - e^{1}}{2 \cdot 1 - e^{1}} \\[0.8em] &= 1 - \frac{3 - e}{2 - e} \\[0.8em] &\approx 1{,}39 \end{align*}\]
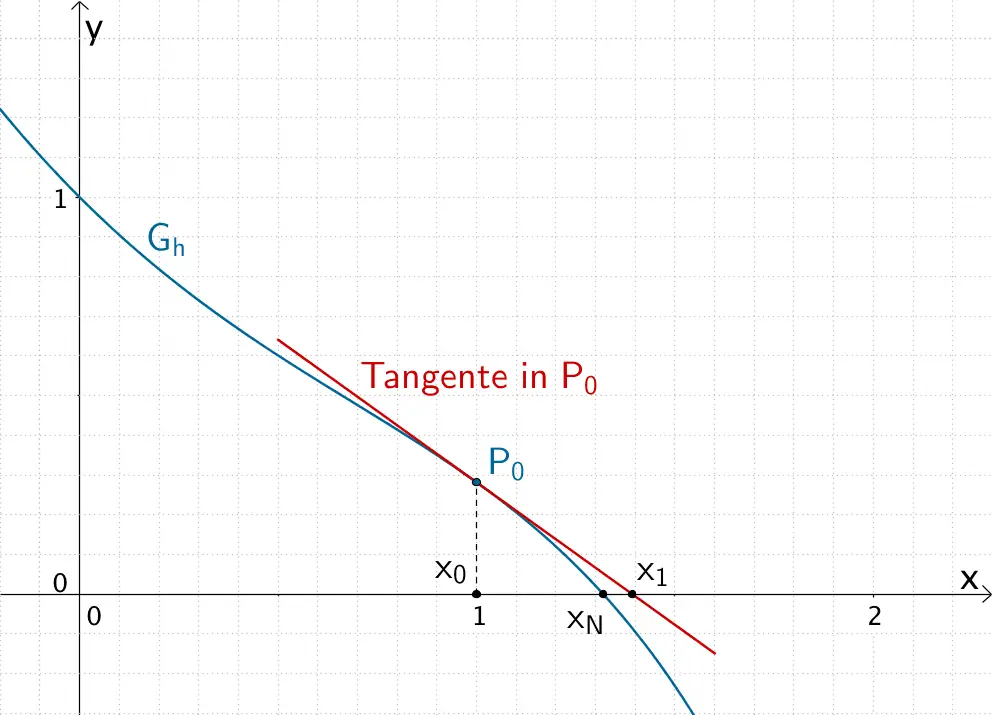
Erster Schritt des Newton-Verfahrens mit dem Startwert \(x_{0} = 1\) und dem Näherungswert \(x_{1}\) für die Lösung der Gleichung \(h(x) = 0\)


