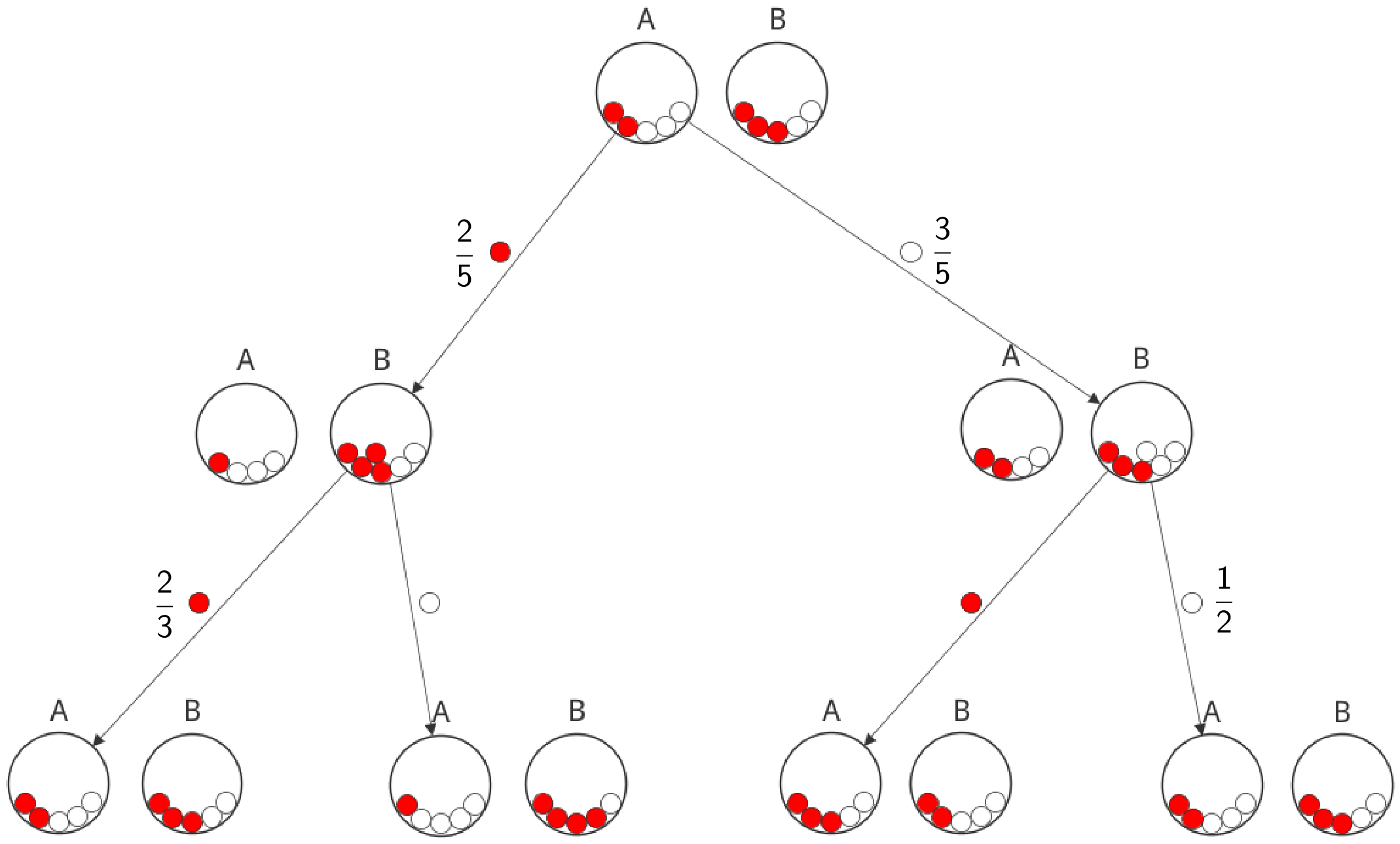
Betrachtet wir das Ereignis \(E\): „Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A." Untersuchen Sie, ob das Ereignis \(E\) eine größere Wahrscheinlichkeit als sein Gegenereignis hat.
(3 BE)
Lösung zu Teilaufgabe 1b
\(E\): „Nach der Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A."
Für die beiden Fälle, dass im ersten Durchgang aus Urne A und im zweiten Durchgang aus Urne B jeweils eine rote Kugel oder jeweils eine weiße Kugel entnommen wird, befinden sich nach der Durchführung des Zufallsexperiments wieder drei weiße Kugeln in Urne A (siehe Teilaufgabe 1a).
Baumdiagramm mit den für das Ereignis \(E\) relevanten Wahrscheinlichkeiten
Wahrscheinlichkeit \(P(E)\) berechnen:
\[P(E) = P(\{rrwww\})\]
\(r\): rote Kugel, \(w\): weiße Kugel
Anwenden der 1. und 2. Pfadregel:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(E) &= P(\{rrwww\}) \\[0.8em] &= \frac{2}{5} \cdot \frac{2}{3} + \frac{3}{5} \cdot \frac{1}{2} \\[0.8em] &= \frac{4}{15} + \frac{3}{10} \\[0.8em] &= \frac{8}{30} + \frac{9}{30} \\[0.8em] &= \frac{17}{30}\end{align*}\]
\[\Longrightarrow \quad P(E) > 0{,}5\]
Es gilt: \(P(E) + P(\overline{E}) = 1\)
\(\Longrightarrow \quad\) Das Ereignis \(E\) hat eine größere Wahrscheinlichkeit als sein Gegenereignis \(\overline{E}\).