Baumdiagramm

In einer Urne befinden sich 20 Kugeln, darunter 12 weiße Kugeln und 8 rote Kugeln. Aus der Urne werden nacheinander zwei Kugeln ohne Zurücklegen entnommen.

Die Zufallsgröße \(X\) beschreibt die Anzahl der entnommenen roten Kugeln.

a) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm.

b) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) und geben Sie diese tabellarisch an.

c) Ermitteln Sie den Erwartungswert und die Standardabweichung der Zufallsgröße \(X\).

d) Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert annimmt, der höchstens um die einfache Standardabweichung vom Erwartungswert abweicht.

Aufgabe 1

Geben Sie von folgenden Funktionen jeweils die maximale Definitionsmenge an und bestimmen Sie jeweils die Nullstelle(n). Bilden Sie jeweils die Ableitungsfunktion und vereinfachen Sie soweit wie möglich.

a) \(f(x) = 2\ln{(3\sqrt{x})}\)

b) \(g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\)

c) \(h(x) = x^{3} \cdot \sin{\left( \dfrac{\pi}{3}x \right)}\)

 

Aufgabe 2

Gegeben ist die Funktion \(f \colon x \mapsto \ln{\left( -\dfrac{3}{x} \right)}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.

a) Bestimmen Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs \(D_{f}\).

b) Zeigen Sie durch Rechnung, dass \(G_{f}\) in \(D_{f}\) linksgekrümmt ist.

 

Aufgabe 3

 

Aufgabe 4

Gegeben sind die Kugel \(K_{1}\) mit dem Mittelpunkt \(M_{1}(-3|5|8)\) und dem Radius \(r_{1} = 3\) sowie die Kugel \(K_{2}\) mit dem Mittelpunkt \(M_{2}(7|-5|3)\) und dem Radius \(r_{2} = 7\).

Untersuchen Sie die gegenseitige Lage der Kugeln \(K_{1}\) und \(K_{2}\) und berechnen Sie ggf. den Abstand der beiden Kugeln.

 

Aufgabe 5

Bei der Herstellung wiederaufladbarer Batterien treten zwei Fehler auf.

\(A\): Die Abmessung der Batterie weicht von der Typennorm ab.

\(L\): Die Ladekapazität der Batterie liegt 20 % unter dem Sollwert.

Laut Qualitätskontrolle weisen 15 % der Batterien den Fehler \(L\) auf und 5 % den Fehler \(A\). Die Wahrscheinlichkeit, dass mindestens einer der beiden Fehler auftritt, wird mit 17 % angegeben.

a) Beschreiben Sie folgende Ereignisse im Sachzusammenhang:

α) \(\overline{\overline{A} \cap \overline{L}}\)

β) \((A \cap \overline{L}) \cup (\overline{A} \cap L)\)

b) Erstellen Sie eine den Sachverhalt beschreibende vollständig ausgefüllte Vierfeldertaffel.

c) Zeigen Sie dass die Ereignisse \(A\) und \(L\) stochastisch abhängig sind.

d) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm, beginnend mit dem Ereignis \(A\). Beschreiben Sie, woran sich die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) an diesem Baumdiagramm erkennen lässt.

Ein Laplace-Tetraeder (dreiseitige Pyramide mit vier kongruenten gleichseitigen Dreiecken) ist auf seinen vier Flächen mit je einer der Ziffern 1 bis 4 beschriftet. Es wird folgendes Spiel gespielt:

Ein Spieler zahlt einen Einsatz in Höhe von 1 Euro. Dann setzt er auf eine der Ziffern 1, 2, 3 oder 4 und wirft das Tetraeder anschließend dreimal. Gewertet wird die Ziffer der Fläche, auf der das Tetraeder zu liegen kommt.

Erzielt der Spieler bei keinem Wurf die gesetzte Ziffer, ist der Einsatz verloren.

Erzielt der Spieler einmal die gesetzte Ziffer, erhält er den Einsatz zurück.

Erzielt der Spieler zweimal die gesetzte Ziffer, erhält er den doppelten Einsatz zurück.

Erzielt der Spieler dreimal die gesetzte Ziffer, erhält er den dreifachen Einsatz zurück.

Die Zufallsgröße \(G\) beschreibt den Gewinn eines Spielers pro Spiel in Euro.

a) Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\).

b) Berechnen Sie den Erwartungswert der Zufallsgröße \(G\) und interpretieren Sie das Ergebnis im Sachzusammenhang.

In einer Urne befinden sich eine gelbe und zwei blaue Kugeln. Es werden nacheinander drei Kugeln gezogen und deren Farbe notiert. Die gezogene Kugel wird jeweils zurückgelegt und zwei weitere Kugeln derselben Farbe in die Urne gegeben. Die Zufallsgröße \(X\) beschreibt die Anzahl der gezogenen gelben Kugeln.

a) Erstellen Sie ein vollständig beschriftetes Baumdiagramm und geben Sie den Ergebnisraum an.

b) Berechnen Sie die Wahrscheinlichkeit \(P(X \geq 1)\).

c) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit sich mithilfe des Terms \(1 - P(X = 3)\) berechnen lässt.

Bei der Herstellung wiederaufladbarer Batterien treten zwei Fehler auf.

\(A\): Die Abmessung der Batterie weicht von der Typennorm ab.

\(L\): Die Ladekapazität der Batterie liegt 20 % unter dem Sollwert.

Laut Qualitätskontrolle weisen 15 % der Batterien den Fehler \(L\) auf und 5 % den Fehler \(A\). Die Wahrscheinlichkeit, dass mindestens einer der beiden Fehler auftritt, wird mit 17 % angegeben.

a) Beschreiben Sie folgende Ereignisse im Sachzusammenhang:

α) \(\overline{\overline{A} \cap \overline{L}}\)

β) \((A \cap \overline{L}) \cup (\overline{A} \cap L)\)

b) Erstellen Sie eine den Sachverhalt beschreibende vollständig ausgefüllte Vierfeldertaffel.

c) Zeigen Sie dass die Ereignisse \(A\) und \(L\) stochastisch abhängig sind.

d) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm, beginnend mit dem Ereignis \(A\). Beschreiben Sie, woran sich die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) an diesem Baumdiagramm erkennen lässt.

Aufgabe 1

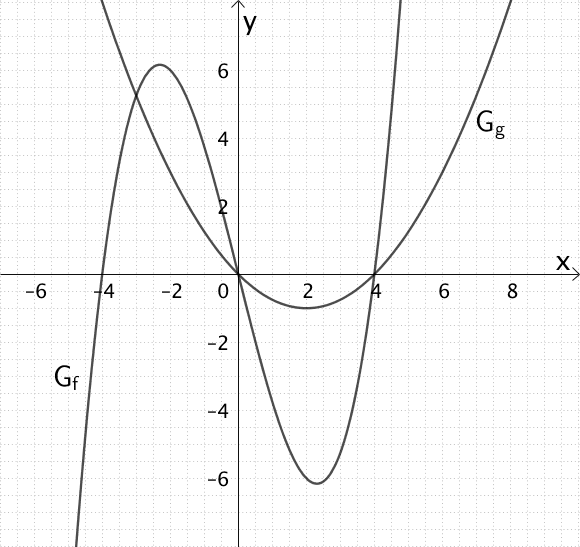
Gegeben sind die Funktionen \(f \colon x \mapsto \dfrac{1}{4}x^{3} - 4x\) und \(g \colon x \mapsto \dfrac{1}{4}x^{2} - x\). Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f\) sowie den Graphen \(G_{g}\) der Funktion \(g\).

a) Berechnen Sie den Flächeninhalt \(A\) der von den Graphen \(G_{f}\) und \(G_{g}\) begrenzten Fläche.

b) Geben Sie ohne weitere Rechnung den Wert des Integrals \(\displaystyle \int_{-4}^{+4} f(x) dx\) an und veranschaulichen Sie Ihr Ergebnis in der Abbildung durch geeignete Eintragungen.

 

Aufgabe 2

Geben ist die Integralfunktion \(\displaystyle I \colon x \mapsto \int_{1}^{x} \ln{(3t - 2)} dt\).

a) Geben Sie den maximalen Definitionsbereich der Integralfunktion \(I\) an.

b) Berechnen Sie eine integralfreie Darstellung der Integralfunktion \(I\). Vereinfachen Sie soweit wie möglich.

 

Aufgabe 3

Die Kurvendiskussion einer ganzrationalen Funktion \(f\) ergibt folgende Gleichungen:

\(f'(2) = 0; \; f''(2) = 0\)

a) Entscheiden Sie, welche der drei Aussagen richtig ist und begründen Sie Ihre Wahl.

(I) An der Stelle \(x = 2\) hat der Graph der Funktion \(f\) einen Extrempunkt.

(II) An der Stelle \(x = 2\) hat der Graph der Funktion \(f\) einen Terrassenpunkt.

(III) An der Stelle \(x = 2\) hat der Graph der Funktion \(f\) einen Extrem- oder Terrassenpunkt.

b) Bestimmen Sie einen möglichen Funktionsterm \(f(x)\), sodass der Graph der Funktion \(f\) an der Stelle \(x = 2\) einen Terrassenpunkt besitzt.

 

Aufgabe 4

In einer Urne befinden sich 20 Kugeln, darunter 12 weiße Kugeln und 8 rote Kugeln. Aus der Urne werden nacheinander zwei Kugeln ohne Zurücklegen entnommen.

Die Zufallsgröße \(X\) beschreibt die Anzahl der entnommenen roten Kugeln.

a) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm.

b) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) und geben Sie diese tabellarisch an.

c) Ermitteln Sie den Erwartungswert und die Standardabweichung der Zufallsgröße \(X\).

d) Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert annimmt, der höchstens um die einfache Standardabweichung vom Erwartungswert abweicht.

 

Aufgabe 5

a) Berechnen Sie den Einsatz des Spiels, sodass das Spiel „fair" ist.

b) Der Einsatz des Spiels beträgt nun 1 €. Wie sind die Öffnungswinkel der Sektoren des Glücksrads zu wählen, damit das Spiel „fair" ist?

Von den im einleitenden Text angegebenen Zahlenwerten soll nur der Prozentsatz 40 % so geändert werden, dass die Ereignisse \(A\) und \(R\) unabhängig sind. Geben Sie den geänderten Wert an.

(2 BE)

Begründen Sie, dass die Ereignisse \(A\) und \(R\) abhängig sind.

(2 BE)

Erstellen Sie zu der beschriebenen Situation ein vollständig beschriftetes Baumdiagramm oder eine vollständig ausgefüllte Vierfeldertafel.

(4 BE)

Keimt ein Samenkorn, so wächst daraus eine Pflanze heran, die aufgrund schädlicher Einflüsse jedoch in manchen Fällen keine Gurken trägt. Bei einem gekeimten Samenkorn der Qualität A entsteht mit einer Wahrscheinlichkeit von 85 % eine fruchtragende Pflanze, bei einem gekeimten Samenkorn der Qualität B mit einer Wahrscheinlichkeit von 75 %. Vereinfachend wird davon ausgegangen, dass - unabhängig von der Qualität der Samenkörner - von jeder fruchtragenden Pflanze gleich viele Gurken geerntet werden können.

Ein Samenkorn der Qualität A kostet 17 Cent, eines der Qualität B 12 Cent. Entscheiden Sie durch Rechnung, ob es für einen Anbaubetrieb finanziell günstiger ist, sich auf Samenkörner der Qualität A zu beschränken, oder ob es finanziell günstiger ist, sich auf Samenkörner der Qualität B zu beschränken, wenn er alle Gurken zum selben Preis verkauft.

(5 BE)

Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl \((Z)\) oder zum zweiten Mal Wappen \((W)\) oben liegt. Als Ergebnismenge wird festgelegt: \(\{ZZ; WW; ZWZ; ZWW; WZZ; WZW\}\).

Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.

(2 BE)

Neben dem Fußballturnier werden für die Schülerinnen und Schüler auch ein Elfmeterschießen und ein Torwandschießen angeboten.

Dafür konnten sich Kinder in zwei Listen eintragen. 45 % der Kinder haben sich sowohl für das Torwandschießen als auch für das Elfmeterschießen eingetragen, 15 % haben sich nur für das Elfmeterschießen eingetragen. 90 % der Kinder, die sich für das Torwandschießen eingetragen haben, haben sich auch für das Elfmeterschießen eingetragen. Aus den Kindern wird eines zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:

\(T\): „Das Kind hat sich für das Torwandschießen eingetragen."

\(E\): „das Kind hat sich für das Elfmeterschießen eingetragen."

Untersuchen Sie die Ereignisse \(T\) und \(E\) auf stochastiche Unabhängigkeit.

(4 BE)

Betrachtet wir das Ereignis \(E\): „Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A." Untersuchen Sie, ob das Ereignis \(E\) eine größere Wahrscheinlichkeit als sein Gegenereignis hat.

(3 BE)

Betrachtet wir das Ereignis \(E\): „Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A." Untersuchen Sie, ob das Ereignis \(E\) eine größere Wahrscheinlichkeit als sein Gegenereignis hat.

(3 BE)

Tatsächlich ist der Anteil der Beschäftigten mit einem Jobticket an beiden Standorten unterschiedlich; am Standort B besitzt nur die Hälfte der Beschäftigten ein Jobticket. Berechnen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers, der ein Jobticket besitzt, am Standort A arbeitet.

(3 BE) 

Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen \(A\) und \(B\) sowie deren Gegenereignissen \(\overline{A}\) und \(\overline{B}\) dar.

Bestimmen Sie den Wert von \(p\) so, dass das Ereignis \(B\) bei diesem Zufallsexperiment mit der Wahrscheinlichkeit \(0,3\) eintritt.

(2 BE)

Ein Großhändler bietet Samenkörner für Salatgurken in zwei Qualitätsstufen an. Ein Samenkorn der höheren Qualität A keimt mit einer Wahrscheinlichkeit von 95 %, eines der Qualität B mit einer Wahrscheinlichkeit von 70 %. Ein Anbaubetrieb kauft Samenkörner beider Qualitätsstufen, 65 % aller gekauften Samenkörner sind von der Qualität A.

In einem Gedankenexperiment werden die eingekauften Samenkörner zusammengeschüttet und gemischt. Bestimmen Sie mithilfe eines beschrifteten Baumdiagramms

α) die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn keimt;

β) die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn, das nach der Saat keimt, von der Qualität B ist.

(5 BE)