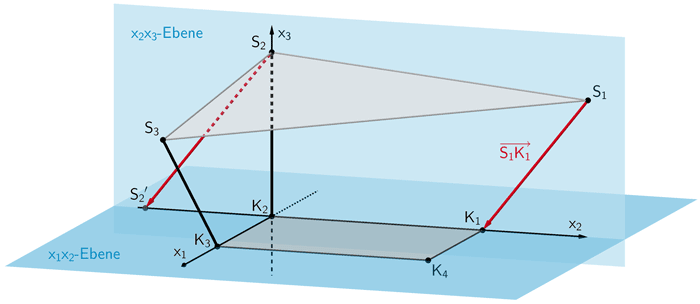
Auf das Sonnensegel fallen Sonnenstrahlen, die im Modell und in der Abbildung 1 durch parallele Geraden mit dem Richtungsvektor \(\overrightarrow{S_{1}K_{1}}\) dargestellt werden können. Das Sonnensegel erzeugt auf dem Boden einen dreieckigen Schatten. Die Schatten der mit \(S_{2}\) bzw. \(S_{3}\) bezeichneten Ecken des Sonnensegels werden mit \({S_{2}}'\) bzw. \(S_{3}'\) bezeichnet.
Begründen Sie ohne weitere Rechnung, dass \({S_{2}}'\) auf der \(x_{2}\)-Achse liegt.
(2 BE)
Lösung zu Teilaufgabe c
Kurze Argumentation:
Die Punkte \(K_{1}(0|4|0)\), \(S_{1}(0|6|2{,}5)\) und \(S_{2}(0|0|3)\) liegen mit jeweils \(x_{1} = 0\) in der \(x_{2}x_{3}\)-Ebene. Da die Gerade \(S_{2}{S_{2}}'\) außerdem parallel zur Geraden \(S_{1}K_{1}\) verläuft, liegt \({S_{2}}'\) ebenfalls in der \(x_{2}x_{3}\)-Ebene. Zudem liegt \({S_{2}}'\) in der \(x_{1}x_{2}\)-Ebene (Boden, vgl. Angabe).
Der Punkt \({S_{2}}'\) liegt also in der \(x_{2}x_{3}\)-Ebene und in der \(x_{1}x_{2}\)-Ebene. Die \(x_{2}\)-Achse bildet die Menge aller gemeinsamen Punkte der beiden Koordinatenebenen (Schnittgerade). Folglich liegt \({S_{2}}'\) auf der \(x_{2}\)-Achse.
Ausführliche Argumentation:
Als Schattenpunkt liegt \({S_{2}}'\) auf dem Boden. Dieser wird laut Angabe durch die \(x_{1}x_{2}\)-Ebene beschrieben. Also liegt \({S_{2}}'\) in der \(x_{1}x_{2}\)-Ebene.
Die \(\textcolor{#0087c1}{x_{1}}\)-Koordinate der Punkte \(S_{1}(\textcolor{#0087c1}{0}|6|2{,}5)\) und \(K_{1}(\textcolor{#0087c1}{0}|4|0)\) ist jeweils gleich Null. Somit liegen beide Punkte in der \(\textcolor{#0087c1}{x_{2}x_{3}}\)-Ebene. Das bedeutet, dass der Verschiebungsvektor \(\overrightarrow{S_{1}K_{1}} = \begin{pmatrix} 0 \\ -2 \\ -2{,}5 \end{pmatrix}\) einen betrachteten Punkt parallel zur \(x_{2}x_{3}\)-Ebene verschiebt, aber nicht in \(x_{1}\)-Richtung.
Der Punkt \(S_{2}(0|0|3)\) liegt ebenfalls in der \(x_{2}x_{3}\)-Ebene und wird mit dem Verschiebungsvektor \(\overrightarrow{S_{1}K_{1}}\) in dieser Ebene auf den Schattenpunkt \({S_{2}}'\) abgebildet. Da \({S_{2}}'\) zudem in der \(x_{1}x_{2}\)-Ebene liegt (Boden), muss \({S_{2}}'\) auf der \(x_{2}\)-Achse liegen, denn die \(x_{2}\)-Achse ist die Schnittgerade der beiden Koordinatenebenen.


