Berechnen Sie die mittlere Steigung des Graphen von \(f\) im Bereich \(-1 \leq x \leq 1\) auf Hundertstel genau und bestimmen Sie grafisch die Steigung des Graphen von \(f\) in seinem Wendepunkt.
(5 BE)
Lösung zu Teilaufgabe 1b
\[f(x) = \frac{4}{1+e^x};\;D_f = \mathbb R\]
Mittlere Steigung des Graphen von \(f\) im Bereich \(-1 \leq x \leq 1\)
Zu bestimmen ist die Steigung der Sekante durch die Graphenpunkte \((-1|f(-1))\) und \((1|f(1))\).
\[\begin{align*}\frac{f(1) - f(-1)}{1 - (-1)} &= \frac{\frac{4}{1+e^1} - \frac{4}{1+ e^{-1}}}{2} \\[0.8em] &= \frac{2}{1+e} + \frac{2}{1+e^{-1}} \\[0.8em] &\approx -0{,}92\end{align*}\]
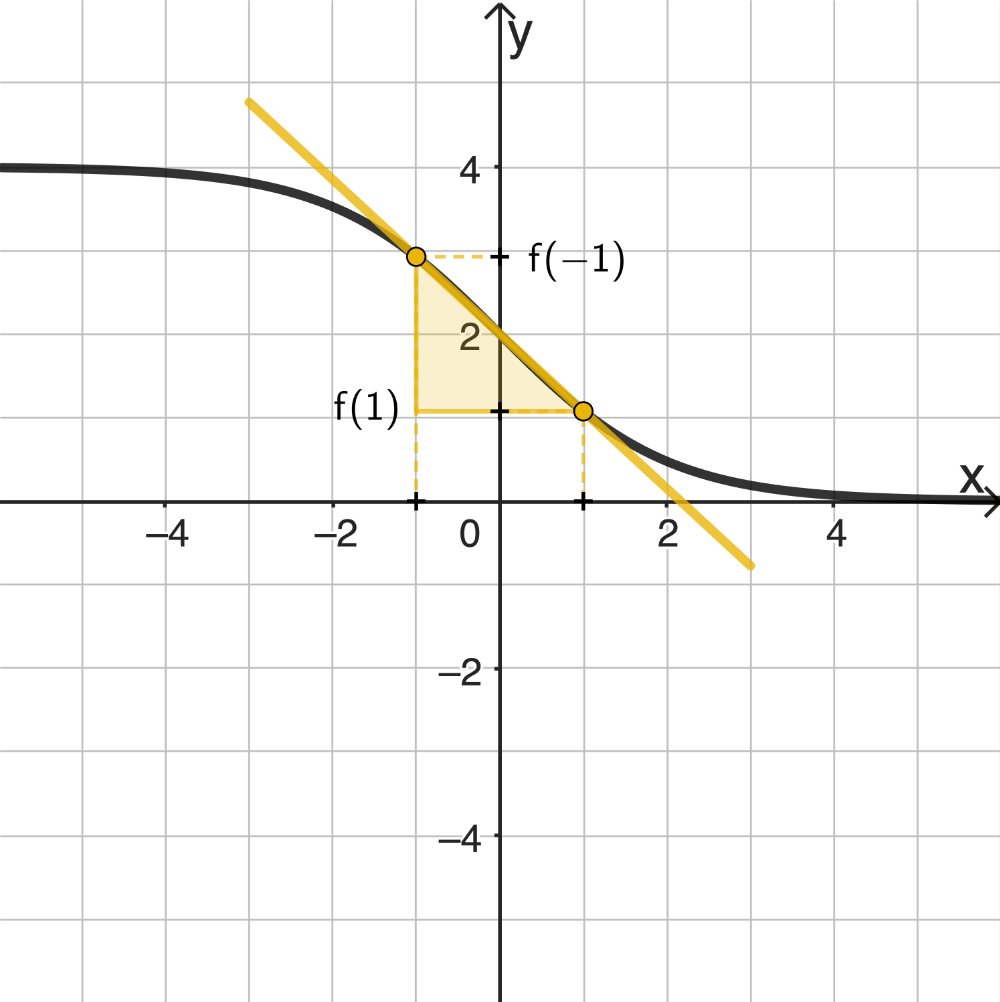ergänzende Skizze
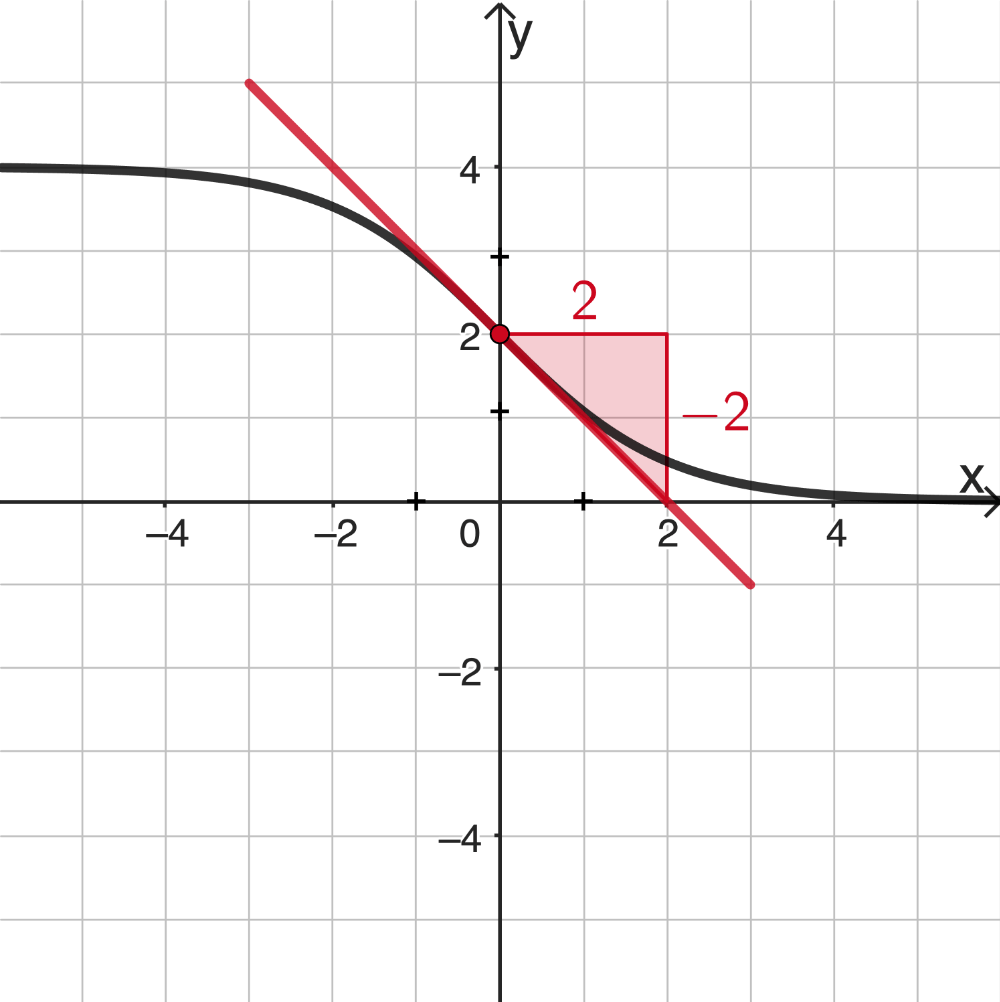
Grafische Bestimmung der Steigung des Graphen von \(f\) in seinem Wendepunkt
Es ist die Steigung der Wendetangente im Wendepunkt \(\textcolor{#cc071e}{(0|2)}\) (vgl. Angabe Aufgabe 1) grafisch zu bestimmen, beispielsweise mithilfe eines geeigneten Steigungsdreiecks.
Mithilfe der Abbildung ergibt sich:
\[\textcolor{#cc071e}{m} \approx \frac{\textcolor{#cc071e}{-2}}{\textcolor{#cc071e}{2}} = \textcolor{#cc071e}{-1}\]
Die Steigung des Graphen von \(f\) in seinem Wendepunkt beträgt etwa \(-1\).
