Abbildung 2 zeigt ein quaderförmiges Möbelstück, das 40 cm hoch ist. Es steht mit seiner Rückseite flächenbündig an der Wand unter dem Fenster. Seine vordere Oberkante liegt im Modell auf der Geraden \(k \colon \enspace \overrightarrow X = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\), \(\lambda \in \mathbb R\,\).
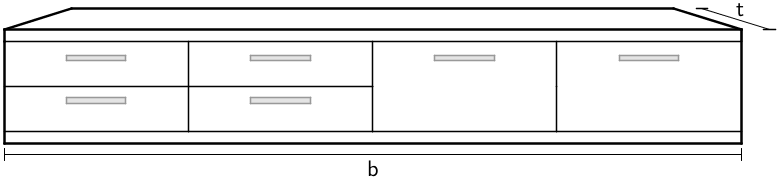Abb. 2
Ermitteln Sie mithilfe von Abbildung 2 die Breite \(b\) des Möbelstücks möglichst genau.
Bestimmen Sie mithilfe der Gleichung der Geraden \(k\) die Tiefe \(t\) des Möbelstücks und erläutern Sie Ihr Vorgehen.
(4 BE)
Lösung zu Teilaufgabe f
Breite \(b\) des Möbelstücks
Abmessen der Höhe in Abbildung 2 liefert:
\[12\;\text{mm} \mathrel{\widehat{=}} 40\;\text{cm}\]
Die Breite misst in Abbildung 2 ca. 78 mm.
Dreisatz anwenden:
\[b = \frac{78\;\text{mm}}{12\;\text{mm}} \cdot 40\;\text{cm} = 260\;\text{cm} = 2{,}6\;\text{m}\]
Tiefe \(t\) des Möbelstücks
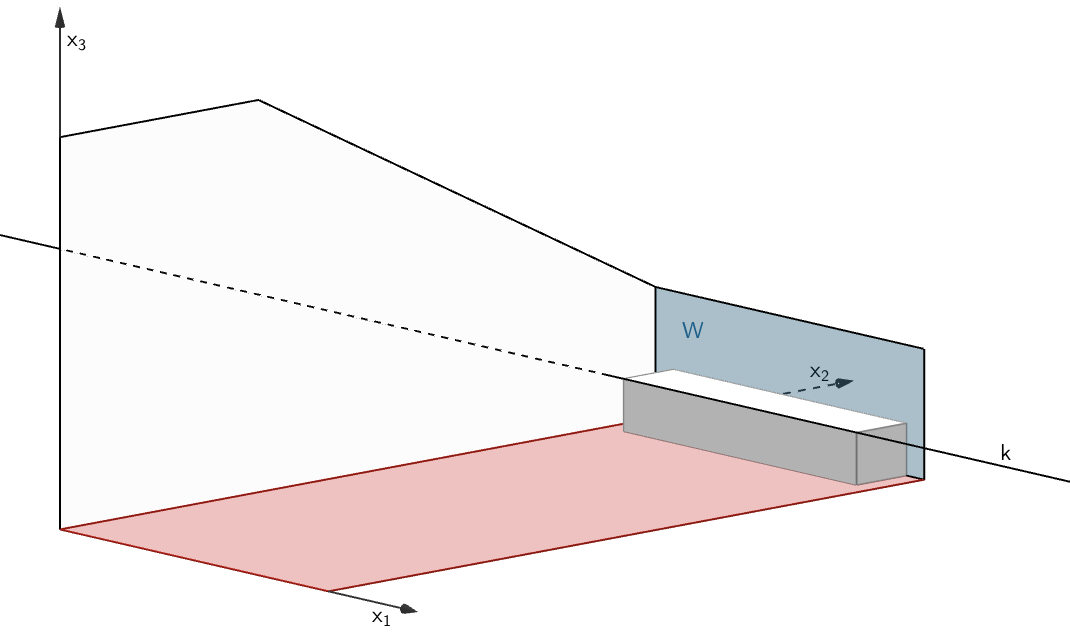
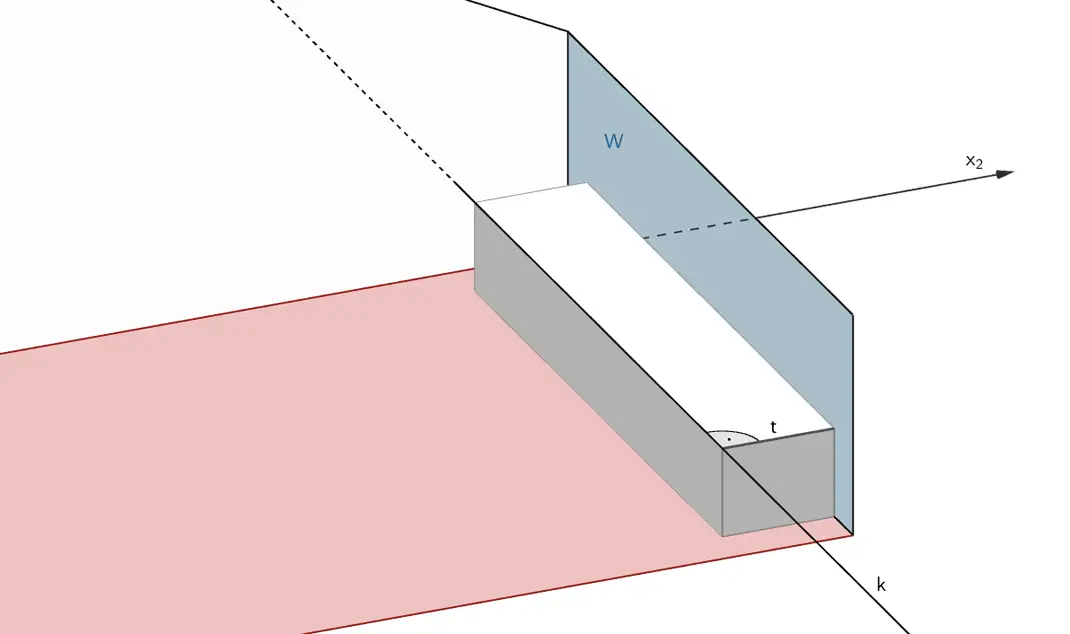
Die Tiefe \(t\) des Möbelstücks entspricht dem Abstand der Geraden \(k\) von der Ebene \(W\), in der die Wand unter dem Fenster liegt.
\[k \colon \enspace \overrightarrow X = \begin{pmatrix} 0 \\ 5{,}5 \\ 0{,}4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\,, \quad \lambda \in \mathbb R\]
\[t = d\,(k;W)\]
Gleichung der Ebenen \(W\,\):
\[\left. \begin{align*} &W \parallel x_1x_3\text{-Ebene} \\[0.8em] &C\,(3|6|1) \in W \end{align*} \right\} \Longrightarrow \quad W \colon \enspace x_2 = 6 \quad \Longleftrightarrow \quad x_2 - 6 = 0\]
oder:
\[W \perp x_2\text{-Achse} \quad \Longrightarrow \quad \overrightarrow{n}_W = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\]
\[C\,(3|6|1) \in W\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Ebenengleichung in Normalenform in Vektordarstellung aufstellen:
\[\begin {align*} &W \colon \enspace \overrightarrow{n}_W \circ \left( \overrightarrow X - \overrightarrow C \right) = 0 \\[0.8em] &W \colon \; \begin {pmatrix} 0 \\ 1 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 3 \\ 6 \\ 1 \end {pmatrix} \right] = 0 \end {align*}\]
Ebenengleichung in Normalenform in Koordinatendarstellung bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin {pmatrix} 0 \\ 1 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 3 \\ 6 \\ 1 \end {pmatrix} \right] &= 0 \\[0.8em] 0 \cdot (x_1 - 3) + 1 \cdot (x_2 - 6) + 0 \cdot (x_3 - 1) &= 0 \\[0.8em] x_2 - 6 &= 0 \end{align*}\]
\[W \colon \enspace x_2 - 6 = 0 \]
Nachweis, dass gilt \(k \parallel W\,\):
Lagebeziehung von Gerade und Ebene
| \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R \enspace\) und \(\enspace E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\) | |||
| \(\overrightarrow{u} \circ \overrightarrow{n}_{E} = 0 \enspace \Longleftrightarrow \enspace \overrightarrow{u} \perp \overrightarrow{n}_{E}\) | \(\overrightarrow{u} \circ \overrightarrow{n}_{E} \neq 0\) | ||
|
\(A \in E\) \(\Longrightarrow \enspace g \subset E\) \(g\) liegt in der Ebene \(E\)
|
\(A \notin E\) \(\Longrightarrow \quad g \parallel E\) \(g\) verläuft (echt) parallel zur Ebene \(E\) (ggf. Abstand berechnen).
|
\(\Longrightarrow \enspace\)\(g\) schneidet die Ebene \(E\) im Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\) (ggf. Schnittpunkt und/oder Schnitwinkel berechnen). |
|
Richtungsvektor der Geraden \(k\,\): \(\;\overrightarrow{u}_k = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\)
Normalenvektor der Ebene \(W\,\): \(\;\overrightarrow{n}_W = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\)
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{u}_k \circ \overrightarrow{n}_W = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = 1 \cdot 0 + 0 \cdot 1 + 0 \cdot 0 = 0\]
\[\Longrightarrow \quad \overrightarrow{u}_k \perp \overrightarrow{n}_W \quad \Longrightarrow \quad k \parallel W\]
Abstand der Geraden \(k\) von der Ebenen \(W\) bestimmen:
Wegen \(k \parallel W\,\) ist der Abstand \(d\,(k;W)\) der Geraden \(k\) zur Ebene \(W\) gleich dem Abstand eines beliebigen Punktes auf der Geraden \(k\) zur Ebene \(W\,\).
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Betrag des Normalenvektors der Ebene \(W\,\):
\(\vert \overrightarrow{n}_W \vert = \left| \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} \right| = 1\,\)
Hessesche Normalenform der Ebene \(W\):
\[W^{HNF} \colon \enspace x_2 - 6 = 0 \]
\((0|5{,}5|0{,}4) \in k\) (Aufbukt der Geradengleichung von \(g\))
\[d\,(k;W) = \vert 5{,}5 - 6 \vert = 0{,}5 \quad \Longrightarrow \quad t = 0{,}5\]
Das Möbelstück hat die Tiefe \(t = 50\;\text{cm}\,\).
