Beschreiben Sie, wie \(G_{f}\) schrittweise aus dem Graphen der in \(\mathbb R^{+}\) definierten Funktion \(x \mapsto \ln{x}\) hervorgeht. Erklären Sie damit das Monotonieverhalten von \(G_{f}\).
(5 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = 2 - \ln{(x - 1)}; \; D_{f} = \; ]1;+\infty[\]
\[x \mapsto \ln{x}\]
Beschreibung, wie \(G_{f}\) schrittweise aus dem Graphen der in \(\mathbb R^{+}\) definierten Funktion \(x \mapsto \ln{x}\) hervorgeht
Beispielsweise lautet eine schrittweise Beschreibung wie folgt:
1. Schritt: Spiegelung an der \(x\)-Achse
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad x \mapsto -\ln{x}\]
2. Schritt: Verschiebung um \(1\) in \(x\)-Richtung
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Longrightarrow \quad x \mapsto -\ln{(x - 1)}\]
3. Schritt: Verschiebung um \(2\) in \(y\)-Richtung
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Longrightarrow \quad x \mapsto -\ln{(x - 1)} + 2\]
Und somit: \(f(x) = 2 - \ln{(x - 1)}\)
Erklärung des Monotonieverhaltens von \(G_{f}\)
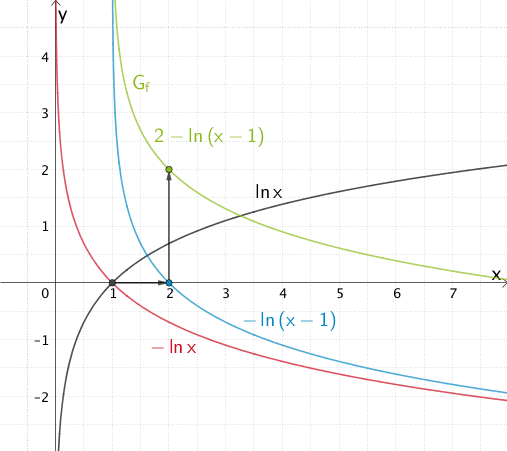
Der Graph der Funktion \(x \mapsto \ln{x}\) ist in \(\mathbb R^{+}\) streng monoton steigend.
Durch die Spiegelung an der \(x\)-Achse ist \(G_{f}\) in \(D_{f}\) streng monoton fallend. Die Verschiebungen haben keinen Einfluss auf das Monotonieverhalten von \(G_{f}\).


