Es wird nun ein bestimmtes Bohrloch im Wasserspeicher betrachtet. Durch das Abfließen verringert sich das Volumen des Wassers im Speicher in Abhängigkeit von der Zeit. Die Funktion \(g \colon t \mapsto 0{,}25t - 25\) mit \(0 \leq t \leq 100\) beschreibt modellhaft die zeitliche Entwicklung dieser Volumenänderung. Dabei ist \(t\) die seit der Fertigstellung des Bohrlochs vergangene Zeit in Sekunden und \(g(t)\) die momentane Änderungsrate des Wasservolumens im Speicher in Litern pro Sekunde.
Berechnen Sie das Volumen des Wassers in Litern, das innerhalb der ersten Minute nach Fertigstellung des Bohrlochs aus dem Behälter abfließt.
(4 BE)
Lösung zu Teilaufgabe k
\[\begin{align*}\int_{0}^{60} g(t) dt &= \int_0^{60} (0{,}25t - 25)dt \\[0.8em] &= \Big[ 0{,}125t^2 - 25t \Big]_0^{60} \\[0.8em] &= 0{,}125 \cdot 60^2 - 25 \cdot 60 \\[0.8em] &= -1050 \end{align*}\]
Innerhalb der ersten Minute nach Fertigstellung des Bohrlochs fließen 1050 Liter aus dem Behälter ab.
Ausführliche Erklärung (nicht verlangt)
\[g(t) = 0{,}25t - 25; \; 0\leq t \leq 100\]
\(g(t)\): Momentane Änderungsrate des Wasservolumens in Litern pro Sekunde
\(t\): Vergangene Zeit in Sekunden seit Fertigstellung des Bohrlochs
Teilaufgabe k behandelt eine wichtige Anwendung der Integralrechnung.
Beschreibt eine Funktion \(f\) die momentane Änderungsrate einer Größe in Abhängigkeit von der Zeit \(t\), so errechnet das bestimmte Integral \(\displaystyle \int_{t_{1}}^{t_{2}}f(t)dt\) den Wert der Gesamtänderung der Größe im Zeitintervall \([t_{1};t_{2}]\).
Differentialquotient oder lokale bzw. momentane Änderungsrate
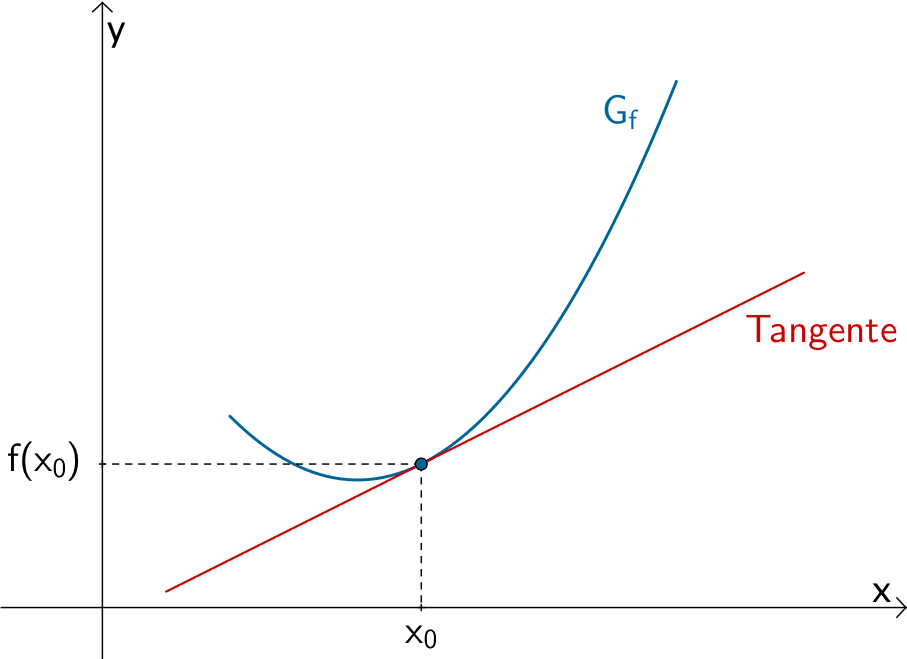
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Das bestimmte Integral \(\displaystyle \int_\textcolor{#0087c1}{0}^{\textcolor{#0087c1}{60}} g(t) dt\) errechnet das Wasservolumen in Litern, welches innerhalb der ersten Minute (ersten 60 Sekunden) nach Fertigstellung des Bohrlochs aus dem Behälter abfließt (negative Gesamtänderung).
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*}\int_{0}^{60} g(t) dt &= \int_0^{60} (0{,}25t - 25)dt &&| \; \int \textcolor{#e9b509}{x^r} dx = \textcolor{#e9b509}{\frac{x^{r + 1}}{r + 1} + C}\enspace (r \neq -1) \\&&&\;\text{(vgl. Merkhilfe)} \\[0.8em] &= \Big[ \textcolor{#e9b509}{\underbrace{0{,}125t^2 - 25t}_{\text{Stammfunktion}}} \Big]_\textcolor{#0087c1}{0}^{\textcolor{#0087c1}{60}} \\[0.8em] &= 0{,}125 \cdot \textcolor{#0087c1}{60}^2 - 25 \cdot \textcolor{#0087c1}{60} - 0 \\[0.8em] &= \textcolor{#cc071e}{-}1050 \end{align*}\]
Innerhalb der ersten Minute nach Fertigstellung des Bohrlochs fließen 1050 Liter aus dem Behälter ab.


