Gegeben ist die Funktion \(f \colon x \mapsto \sqrt{8 - 2x}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie die maximale Definitionsbemenge \(D_{f}\) sowie die Wertemenge \(W_{f}\) der Funktion \(f\) an.
b) Begründen Sie, dass die Funktion \(f\) umkehrbar ist. Bestimmen Sie den Funktionsterm \(f^{-1}(x)\). Geben Sie die Definitions- und die Wertemenge der Umkehrfunktion \(f^{-1}\) an.
c) Der Graph \(G_{f}\) der Funktion \(f\) und der Graph \(G_{f^{-1}}\) der Umkehrfunktion \(f^{-1}\) schließen im ersten Quadranten mit den Koordinatenachsen ein herzförmiges Flächenstück mit dem Flächeninhalt \(A\) ein.
Zeichnen Sie \(G_{f}\) sowie \(G_{f^{-1}}\) mithilfe der Funktionswerte \(f(0)\), \(f(2)\), \(f(3{,}5)\) und \(f(4)\) im ersten Quadranten eines gemeinsamen Koordinatensystems. Achten Sie dabei insbesondere auf den Verlauf von \(G_{f}\) an der Stelle \(x = 4\). Schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\). Berechnen Sie den Flächeninhalt \(A\).
a) Maximale Definitionsbemenge \(D_{f}\) sowie die Wertemenge \(W_{f}\)
Anmerkung:
Die Maximale Definitionsmenge \(D_{f}\) und die Wertemenge \(W_{f}\) sind lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.
Maximale Definitionsmenge \(D_{f}\)
\[f(x) = \sqrt{8 - 2x}\]
Der Radikand (Ausdruck unter der Wurzel) darf nicht negativ sein.
\[\begin{align*} \Longrightarrow \quad 8 - 2x &\geq 0 &&| + 2x \\[0.8em] 8 &\geq 2x &&| : 2 \\[0.8em] 4 &\geq x \end{align*}\]
\[\Longrightarrow \quad D_{f} = \; ]-\infty;4]\]
Wertemenge \(W_{f}\)
\[f(x) = \sqrt{8 - 2x}\]
Es werden die Funktionswerte von \(f\) an den Grenzen des Definitionsbereichs \(D_{f}\) betrachtet.
Für \(x = 4\) nimmt die Funktion \(f\) den kleinstmöglichen Wert \(f(4) = 0\) an.
Für \(x \to -\infty\) gilt:
\[\lim \limits_{x\,\to\,-\infty} f(x) = \lim \limits_{x\,\to\,-\infty} \sqrt{8 - 2x} = +\infty\]
\[\Longrightarrow \quad W_{f} = [0;+\infty[ \; = \mathbb R^{+}_{0}\]
b) Begründung der Umkehrbarhkeit von \(f\) sowie Funktionsterm der Umkehrfunktion \(f^{-1}\) mit Definitions- und die Wertemenge
Begründung der Umkehrbarkeit von \(f\)
Die Funktion \(f\) ist in \(D_{f}\) umkehrbar, wenn der Graph \(G_{f}\) der Funktion \(f\) in \(D_{f}\) entweder streng monoton steigt oder streng monoton fällt (vgl. Abiturskript - 1.5.6 Umkehrfunktion).
Kriterien für die Umkehrbarkeit einer Funktion
Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.
Das Monotonieverhalten von \(G_{f}\) kann mithilfe der ersten Ableitung \(f'\) nachgewiesen werden.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Erste Ableitung \(f'\) bilden:
Die Wurzelfunktion \(f\) lässt sich mithilfe der Ableitung einer Wurzelfunktion bzw. der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel ableiten. Als Alternative kann der Wurzelterm mithilfe der Rechenregegel für Potenzen \(\sqrt[n]{a^{m}} = a^{\frac{m}{n}}\) vorab in der Potenzschreibweise formuliert werden.
\[f(x) = \sqrt{8 - 2x} = (8 - 2x)^{\frac{1}{2}}; \; D_{f} = \; ]-\infty;4]\]
1. Möglichkeit (ohne Formulierung in der Potenzschreibweise):
\[f(x) = \sqrt{8 - 2x}\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[f'(x) = \frac{-\cancel{2}}{\cancel{2}\sqrt{8 - 2x}} = -\frac{1}{\sqrt{8 - 2x}}\]
2. Möglichkeit (nach Formulierung in der Potenzschreibweise):
\[f(x) = (8 - 2x)^{\frac{1}{2}}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}f'(x) &= \frac{1}{2} \cdot (8 - 2x)^{-\frac{1}{2}} \cdot (-2) &&| \; a^{-n} = \frac{1}{a^{n}}; \; a^{\frac{m}{n}} = \sqrt[n]{a^{m}} \\[0.8em] &= \frac{1}{\cancel{2}} \cdot \frac{-\cancel{2}}{\sqrt{8 - 2x}} \\[0.8em] &= -\frac{1}{\sqrt{8 - 2x}} \end{align*}\]
Das Vorzeichen von \(f'(x)\) lässt auf das Monotonieverhalten von \(G_{f}\) schließen.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(\displaystyle f'(x) = -\frac{1}{\underbrace{\sqrt{8 - 2x}}_{> \, 0}}; \; D_{f'} = \; ]-\infty;4[ \quad \Longrightarrow \quad f'(x) < 0\) für \(x \in \; ]-\infty;4[\)
Da \(f'\) an der Stelle \(x = 4\) nicht definiert ist, erfolgt zusätzlich die Grenzwertbetrachtung \(\lim \limits_{x \, \to \, 4^{-}} f'(x)\).
\[\lim \limits_{x \, \to \, 4^{-}} f'(x) = \lim \limits_{x\,\to\,4^{-}} -\frac{1}{\underbrace{\sqrt{8 - 2x}}_{\Large{\to\,0^{+}}}} = -\infty\]
Also fällt \(G_{f}\) in \(D_{f}\) streng monoton und die Funktion \(f\) ist somit in \(D_{f}\) umkehrbar.
Bestimmung des Funktionsterms \(f^{-1}(x)\)
Für die Bestimmung des Funktionsterms \(f^{-1}(x)\) der Umkehrfunktion von \(f\) wird zunächst die Funktionsgleichung \(y = f(x)\) nach der Variablen \(x\) aufgelöst. Anschließend werden die Variablen \(x\) und \(y\) getauscht, wobei nun \(y = f^{-1}(x)\) gilt. Die Schritte lassen sich auch in umgekehrter Reihenfolge ausführen (vgl. Abiturskript - 1.5.6 Umkehrfunktion).
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
\[f(x) = \sqrt{8 - 2x}; \; D_{f} = \; ]-\infty;4]\]
\[\begin{align*} y &= f(x) \\[0.8em] y &= \sqrt{8 - 2x} &&| \; (\dots)^{2} \; (\text{Gleichung quadrieren}) \\[0.8em] y^{2} &= 8 - 2x &&| + 2x - y^{2} \\[0.8em] 2x &= -y^{2} + 8 &&| : 2 \\[0.8em] x &= -0{,}5y^{2} + 4 &&| \; \text{Variablentausch} \\[2.4em] y &= -0{,}5x^{2} + 4 &&| \; y = f^{-1}(x) \\[2.4em] \Longrightarrow \quad f^{-1}(x) &= -0{,}5x^{2} + 4 \end{align*}\]
oder
\[\begin{align*} y &= f(x) \\[0.8em] y &= \sqrt{8 - 2x} &&| \; \text{Variablentausch} \\[2.4em] x &= \sqrt{8 - 2y} &&| \; (\dots)^{2} \; (\text{Gleichung quadrieren}) \\[0.8em] x^{2} &= 8 - 2y &&| + 2y - x^{2} \\[0.8em] 2y &= -x^{2} + 8 &&| : 2 \\[0.8em] y &= -0{,}5x^{2} + 4 &&| \; y = f^{-1}(x) \\[2.4em] \Longrightarrow \quad f^{-1}(x) &= -0{,}5x^{2} + 4 \end{align*}\]
Definitions- und Wertemenge der Umkehrfunktion \(f^{-1}\)
Bei der Umkehrung einer Funktion werden der Definitionsbereich und der Wertebereich miteinander vertauscht (vgl. Abiturskript - 1.5.6 Umkehrfunktion).
\[D_{f^{-1}} = W_{f} = [0;+\infty] = \mathbb R^{+}_{0}\]
\[W_{f^{-1}} = D_{f} = \; ]-\infty;4]\]
c) Zeichnung von \(G_{f}\) und \(G_{f^{-1}}\) sowie Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\), Berechnung des Flächeninhalts \(A\)
Zeichnung von \(G_{f}\) und \(G_{f^{-1}}\) sowie Schraffieren des Flächenstücks mit dem Flächeninhalt \(A\)
Funktionswerte \(f(0)\), \(f(2)\), \(f(3{,}5)\) und \(f(4)\) berechnen:
\[f(x) = \sqrt{8 - 2x}; \; D_{f} = \; ]-\infty;4]\]
\[f(0) = \sqrt{8 - 2 \cdot 0} = \sqrt{8} = 2\sqrt{2} \approx 2{,}8\]
\[f(2) = \sqrt{8 - 2 \cdot 2} = \sqrt{4} = 2\]
\[f(3{,}5) = \sqrt{8 - 2 \cdot 3{,}5} = \sqrt{1} = 1\]
\[f(4) = \sqrt{8 - 2 \cdot 4} = \sqrt{0} = 0\]
Der Graph \(G_{f}\) verläuft also durch die Punkte \((0|2\sqrt{2})\), \((2|2)\), \((3{,}5|1)\) und \((4|0)\).
Zudem wurde in Teilaufgabe b gezeigt, dass \(\lim \limits_{x\,\to\,4^{-}} f'(x) = -\infty\) gilt. Da \(f'\) die Steigung einer Tangente an den Graphen \(G_{f}\) an einer betrachteten Stelle beschreibt, bedeutet dieses Ergebnis, dass \(G_{f}\) an der Stelle \(x = 4\) nahezu senkrecht (unendliche Steigung) auf der \(x\)-Achse mündet.
Der Graph \(G_{f^{-1}}\) der Umkehrfunktion von \(f\) geht durch Spiegelung des Graphen \(G_{f}\) an der Winkelhalbierenden des ersten und dritten Quadranten mit der Gleichung \(y = x\) hervor.
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
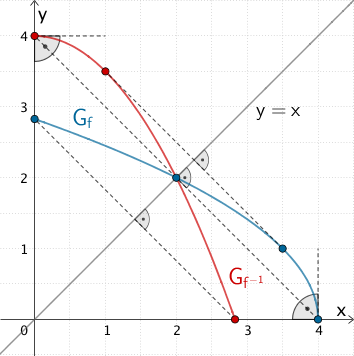
Verlauf des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \sqrt{8 - 2x}; \; D_{f} = \; ]-\infty;4]\) und des an der Winkelhalbierenden \(y = x\) gespiegelten Graphen \(G_{f^{-1}}\) der Umkehrfunktion \(f^{-1} \colon x \mapsto -0{,}5x^{2} + 4; D_{f} = \mathbb R^{+}_{0}\) im ersten Quadranten des Koordinatensystems
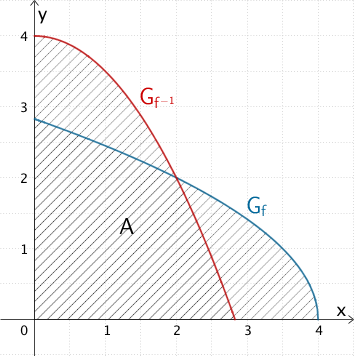
Herzförmiges Flächenstück mit dem Flächeninhalt \(A\), das \(G_{f}\) und \(G_{f^{-1}}\) im ersten Quadranten mit den Koordinatenachsen einschließen.
Berechnung des Flächeninhalts \(A\)
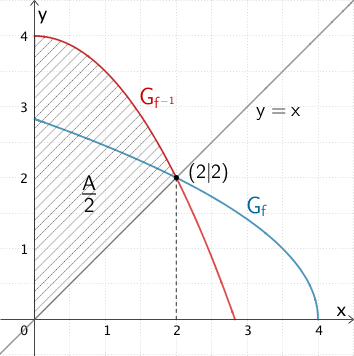
Die Winkelhalbierende \(y = x\) telt das Flächenstück mit dem Flächeninhalt \(A\) in zwei gleich große Teilflächen. Der Punkt \((2|2) \in G_{f}\) liegt auf der Winkelhalbierenden und ist damit Schnittpunkt von \(G_{f}\) und \(G_{f^{-1}}\).
Betrachtet wird beispielsweise der Flächeninhalt \(\frac{A}{2}\) des Flächenstücks, das der Graph \(G_{f^{-1}}\) der Umkehrfunktion \(f^{-1}\) und die Winkelhalbierende \(y = x\) im Intervall \([0;2]\) einschließen. Dann gilt (vgl. Abiturskript - 1.6.4 Flächenberechnung, Flächeninhalt zwischen zwei Funktionsgraphen):
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= 2 \cdot \underbrace{ \int_{0}^{2} \left[ f^{-1}(x) - x \right] dx}_{\Large{\frac{A}{2}}} \\[0.8em] &= 2 \cdot \int_{0}^{2} \left( -0{,}5x^{2} + 4 - x \right) dx \\[0.8em] &= 2 \cdot \int_{0}^{2} \left( -0{,}5x^{2} - x + 4 \right) dx \end{align*}\]
Anmerkung:
Grundsätzlich kann auch der Flächeninhalt \(\frac{A}{2}\) des Flächenstücks betrachtet werden, das die Winkelhalbierende \(y = x\) sowie \(G_{f}\) mit der \(x\)-Achse einschließt. Allerdings muss dann über die Wurzelfunktion \(f\) integriert werden, was den Rechenaufwand (Stammfunktion bestimmen) erhöht.
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{0}^{2} \left( -0{,}5x^{2} - x + 4 \right) dx\) wird eine Stammfunktion der Integrandenfunktion \(x \mapsto -0{,}5x^{2} - x + 4\) benötigt.
Die Menge aller Stammfunktion der Integrandenfunktion \(x \mapsto -0{,}5x^{2} - x + 4\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int \left(-0{,}5x^{2} - x + 4\right) dx\).
Mithilfe des wichtigen unbestimmten Integrals \(\displaystyle \int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \; (r \neq -1)\) ergibt sich:
Wichtiges unbestimmtes Integral:
\[\int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq -1)\]
\[C \in \mathbb R\]
(vgl. Merkhilfe)
\[\begin{align*}\int \left(-0{,}5x^{2} - x + 4\right) dx &= -0{,}5 \cdot \frac{1}{3}x^{3} - \frac{1}{2}x^{2} + 4x + C \\[0.8em] &= -\frac{1}{6}x^{3} - \frac{1}{2}x^{2} + 4x + C \end{align*}\]
Für \(C = 0\) ist die Funktion \(x \mapsto -\frac{1}{6}x^{3} - \frac{1}{2}x^{2} + 4x\) eine Stammfunktion der Integrandenfunktion \(x \mapsto -0{,}5x^{2} - x + 4\).
Damit kann der Flächeninhalt \(A\) wie folgt berechnet werden:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= 2 \cdot \int_{0}^{2} \left( -0{,}5x^{2} - x + 4 \right) dx \\[0.8em] &= 2 \cdot \left[ -\frac{1}{6}x^{3} - \frac{1}{2}x^{2} + 4x \right]_{0}^{2} \\[0.8em] &= 2 \cdot \left[ -\frac{1}{6} \cdot 2^{3} - \frac{1}{2} \cdot 2^{2} + 4 \cdot 2 - \left( -\frac{1}{6} \cdot 0^{3} - \frac{1}{2} \cdot 0^{2} + 4 \cdot 0 \right) \right] \\[0.8em] &= 2 \cdot \left( -\frac{4}{3} - 2 + 8 - 0 \right) \\[0.8em] &= \frac{28}{3} \\[0.8em] &= 9\frac{1}{3} \end{align*}\]
Der Flächeninhalt \(A\) des Flächenstücks, das \(G_{f}\) und \(G_{f^{-1}}\) im ersten Quadranten mit den Koordinatenachsen einschließen, beträgt \(9\frac{1}{3}\) FE (Flächeneinheiten).
Alternative:
![Flächenstücke, welche der Graph der Umkehrfunktion von f bzw. die Winkelhalbierende y = x im Intervall [0;2] mit der x-Achse einschließen. Flächenstücke, welche der Graph der Umkehrfunktion von f bzw. die Winkelhalbierende y = x im Intervall [0;2] mit der x-Achse einschließen.](/images/stories/Klausuren/Klausuren_Q12_2/Klausur_Q12_2-003/Klausur_Q12_2-003_A1_4.png)
Der Flächeninhalt \(\frac{A}{2}\) lässt sich als Differenz der Flächeninhalte der Flächenstücke berechnen, welche \(G_{f^{-1}}\) bzw. die Winkelhalbierende \(y = x\) im Intervall \([0;2]\) mit der \(x\)-Achse einschließen.
Somit kann der Flächeninhalt \(A\) wie folgt berechnet werden:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A &= 2 \cdot \bigg( \underbrace{\int_{0}^{2} f^{-1}(x) dx - A_{\triangle}}_{\Large{\frac{A}{2}}} \bigg) \\[0.8em] &= 2 \cdot \left( \int_{0}^{2} \left( -0{}5x^{2} + 4 \right) dx - \frac{1}{2} \cdot 2 \cdot 2 \right) \\[0.8em] &= 2 \cdot \left( \left[ -\frac{1}{6}x^{3} + 4x \right]_{0}^{2} - 2 \right) \\[0.8em] &= 2 \cdot \left[ -\frac{1}{6} \cdot 2^{3} + 4 \cdot 2 - \left( -\frac{1}{6} \cdot 0^{3} + 4 \cdot 0 \right) - 2 \right] \\[0.8em] &= 2 \cdot \left( -\frac{4}{3} + 8 - 0 - 2 \right) \\[0.8em] &= 2 \cdot \frac{14}{3} \\[0.8em] &= \frac{28}{3} \\[0.8em] &= 9\frac{1}{3} \end{align*}\]
Der Flächeninhalt \(A\) des Flächenstücks, das \(G_{f}\) und \(G_{f^{-1}}\) im ersten Quadranten mit den Koordinatenachsen einschließen, beträgt \(9\frac{1}{3}\) FE (Flächeneinheiten).

